Consider a copper cylinder of volume x, resistivity f, resistance across its length is r. If diameter of cylindrical conductor is (16fxπ2r)1/k , then find the value of k.
The correct Answer is:4
To solve the problem, we need to find the value of k given the diameter of a copper cylinder in terms of its volume, resistivity, and resistance. Let's break down the solution step by step.
Step 1: Understand the given parameters
We have:
- Volume of the cylinder: V=x
- Resistivity of the material: ρ=f
- Resistance across its length: R=r
- Diameter of the cylinder: d=(16fxπ2r)1k
Step 2: Relate volume to diameter and length
The volume V of a cylinder can be expressed as:
V=A⋅l
where A is the cross-sectional area and l is the length of the cylinder. The cross-sectional area A for a cylinder with diameter d is given by:
A=πd24
Thus, we can write:
x=πd24⋅l
Step 3: Solve for length l
Rearranging the equation for volume, we get:
l=4xπd2
Step 4: Use the formula for resistance
The resistance R of a cylindrical conductor is given by:
R=ρlA
Substituting the expressions for l and A:
R=f⋅(4xπd2)πd24
This simplifies to:
R=4fxπd2⋅4πd2=16fxπ2d2
Step 5: Rearranging to find d2
From the equation R=16fxπ2d2, we can express d2 in terms of R:
d2=16fxπ2R
Step 6: Find d
Taking the square root of both sides gives:
d=√16fxπ2R=(16fxπ2R)12
Step 7: Compare with the given diameter expression
We are given:
d=(16fxπ2r)1k
From our derivation, we have:
d=(16fxπ2R)12
Step 8: Equate the two expressions for d
Setting the two expressions for d equal gives:
(16fxπ2R)12=(16fxπ2r)1k
Step 9: Solve for k
From the equality, we can deduce:
12=1k
Thus, solving for k gives:
k=4
Final Answer
The value of k is 4.
---
We have:
- Volume of the cylinder: V=x
- Resistivity of the material: ρ=f
- Resistance across its length: R=r
- Diameter of the cylinder: d=(16fxπ2r)1k
The volume V of a cylinder can be expressed as:
V=A⋅l
where A is the cross-sectional area and l is the length of the cylinder. The cross-sectional area A for a cylinder with diameter d is given by:
A=πd24
Thus, we can write:
x=πd24⋅l
Rearranging the equation for volume, we get:
l=4xπd2
The resistance R of a cylindrical conductor is given by:
R=ρlA
Substituting the expressions for l and A:
R=f⋅(4xπd2)πd24
This simplifies to:
R=4fxπd2⋅4πd2=16fxπ2d2
From the equation R=16fxπ2d2, we can express d2 in terms of R:
d2=16fxπ2R
Taking the square root of both sides gives:
d=√16fxπ2R=(16fxπ2R)12
We are given:
d=(16fxπ2r)1k
From our derivation, we have:
d=(16fxπ2R)12
Setting the two expressions for d equal gives:
(16fxπ2R)12=(16fxπ2r)1k
From the equality, we can deduce:
12=1k
Thus, solving for k gives:
k=4
The value of k is 4.
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - AAKASH SERIESCHAPTER - CURRENT ELECTRICITYEXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL -II PRACTICE SHEET (ADVANCED) (Straight Objective Type Questions))
5 Videos
- CURRENT ELECTRICITYBOOK - AAKASH SERIESCHAPTER - CURRENT ELECTRICITYEXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL -II PRACTICE SHEET (ADVANCED) (More than One correct answer Type Questions))
5 Videos
- CURRENT ELECTRICITYBOOK - AAKASH SERIESCHAPTER - CURRENT ELECTRICITYEXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL -II LECTURE SHEET (ADVANCED) (Matrix Matching Type Questions))
2 Videos
- CURRENT ELECTRICITYBOOK - AAKASH SERIESCHAPTER - CURRENT ELECTRICITYEXERCISE - PROBLEMS (LEVEL-II)
27 Videos
- DUAL NATURE OF RADIATION AND MATTERBOOK - AAKASH SERIESCHAPTER - DUAL NATURE OF RADIATION AND MATTEREXERCISE - PRACTICE EXERCISEX
42 Videos
Similar Questions
Knowledge Check
When a resistance of 100Ω is connected in series with a galvanometer of resistance R, then its range is V. To double its range, a resistance of 1000Ω is connected in series. Find the value of R.
A1100B1000C900D800
Consider a wire of length l, area of cross section A, and resistivity ρ with resistance 10Ω. Its length is increased by applying a force, and it becomes four times of its original value. Find the changed resistance of the wire.
View Solution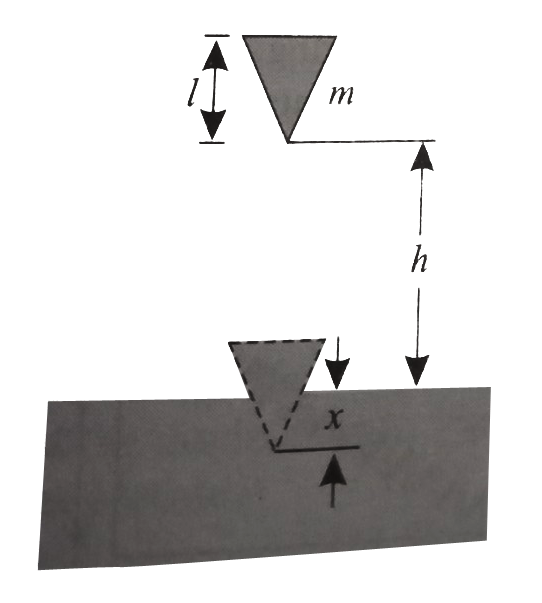
A cone of mass m falls from a height h and penetrates into sand. The resistance force R of the sand is given by R=kx2. If the cone penetrates up to a distance x=d where d<λ, then find the value of k.
View SolutionA long round conductor of cross-sectional area S is made of material whose resistivity depends only on a distance r from the axis of the conductor as ρ=α/r2, where α is a constant. Find the total resistance per unit length of the rod when potential difference is applied across its length.
View SolutionA copper wire of length l and radius r is nickel plated till its final radius is 2r. If the resistivity of the copper and nickel are ρc and ρn, then find the equivalent resistance of the wire.
View SolutionA hemispherical network of radius a is made by using a conducting wire of resistance per unit length 'r' The equivalent resistance across OP is given by [π+n8] ar the value of n will be.

View SolutionA wire of length l has a resistance R. If half of the length is stretched to make the radius half of its original value, then the final resistance of the wire is

View SolutionWhen a resistance of 100Ω is connected in series with a galvanometer of resistance R, then its range is V. To double its range, a resistance of 1000Ω is connected in series. Find the value of R.
View Solution