A 4μF capacitor is charged by a 200 V battery. It is then disconnected from the supply and is connected to another uncharged 2μF capacitor. During the process loss of energy (in J) s
Zero
5.33×10−2
4×10−2
2.67×10−2
The correct Answer is:D
Step by step video & image solution for A 4muF capacitor is charged by a 200 V battery. It is then disconnected from the supply and is connected to another uncharged 2muF capacitor. During the process loss of energy (in J) s by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Related Playlists
- BOOK - AAKASH SERIESCHAPTER - CAPACITORS EXERCISE - PRACTICE SHEET (EXERCISE - III) (LEVEL - II (ADVANCED)) (More than One correct answer Type Questions)7videos
CAPACITORS
- BOOK - AAKASH SERIESCHAPTER - CAPACITORS EXERCISE - PRACTICE SHEET (EXERCISE - III) (LEVEL - II (ADVANCED)) (Linked Comprehension Type Questions)6videos
CAPACITORS
- BOOK - AAKASH SERIESCHAPTER - CAPACITORS EXERCISE - PRACTICE SHEET (EXERCISE - II) (LEVEL - II (ADVANCED)) (Straight Objective Type Questions)5videos
CAPACITORS
- BOOK - AAKASH SERIESCHAPTER - ATOMSEXERCISE - PRACTICE EXERCISE21videos
ATOMS
- BOOK - AAKASH SERIESCHAPTER - COMMUNICATION SYSTEM EXERCISE - LECTURE SHEET (LEVEL - I) (MAIN) (EXERCISE - IV) (Straight Objective & More than one Correct Answer Type Questions)20videos
COMMUNICATION SYSTEM
Similar Questions
A 4μF capacitor is charged by a 200 V supply. It is then disconnected from the supply and is connected to another uncharged 2μF capacitor. How much electrostatic energy of the first capacitor is dissipated in the form of heat and electromagnetic radiation ?
View SolutionA 600pF capacitor is charged by a 200V supply. It is then disconnected from the supply and is connected to another uncharged 600pF capacitor. What is the common potential in V and energy lost in J afrte reconnection?
View SolutionA 600pF capacitor is charged by a 200V supply. It is then disconnected from the supply and is connected to another uncharged 600pF capacitor. What is the common potential in V and energy lost in J after reconnection?
View SolutionA 5μF capacitor is charged fully by a 220 V supply. It is then disconnected from the supply and is connected in series to another uncharged 2.5 μF capacitor . If the energy change during the charge redistribution is X100 J then value of X to the nearest interger is ________.
View SolutionA capacitor C is charged to a potential V by a battery. It is then disconnected from the battery and again connected with its polarity reversed to the battery
View SolutionA capacitor of 60 pF charged to 20 volt. Now battery is removed and then this capacitor is connected to another identical uncharged capacitor. Find heat loss in nJ
View SolutionA capacitor of 60 pF charged to 20 volt. Now battery is removed and then this capacitor is connected to another identical uncharged capacitor. Find heat loss in nJ
View SolutionThe charge on the 4μF capacitor in the steady state is
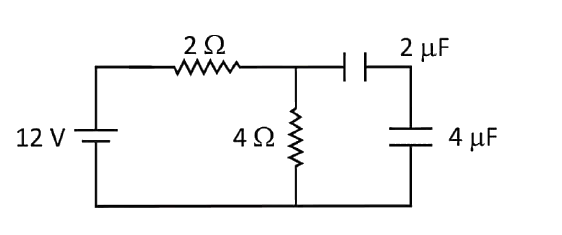 View Solution
View SolutionA capacitor of capacitance value 1μF is charged to 30 V and the battery is then disconnected. If it is connected across a 2μF capacotor, then the energy lost by the system is
View SolutionFind the charges on 6μF and 4μF capacitors
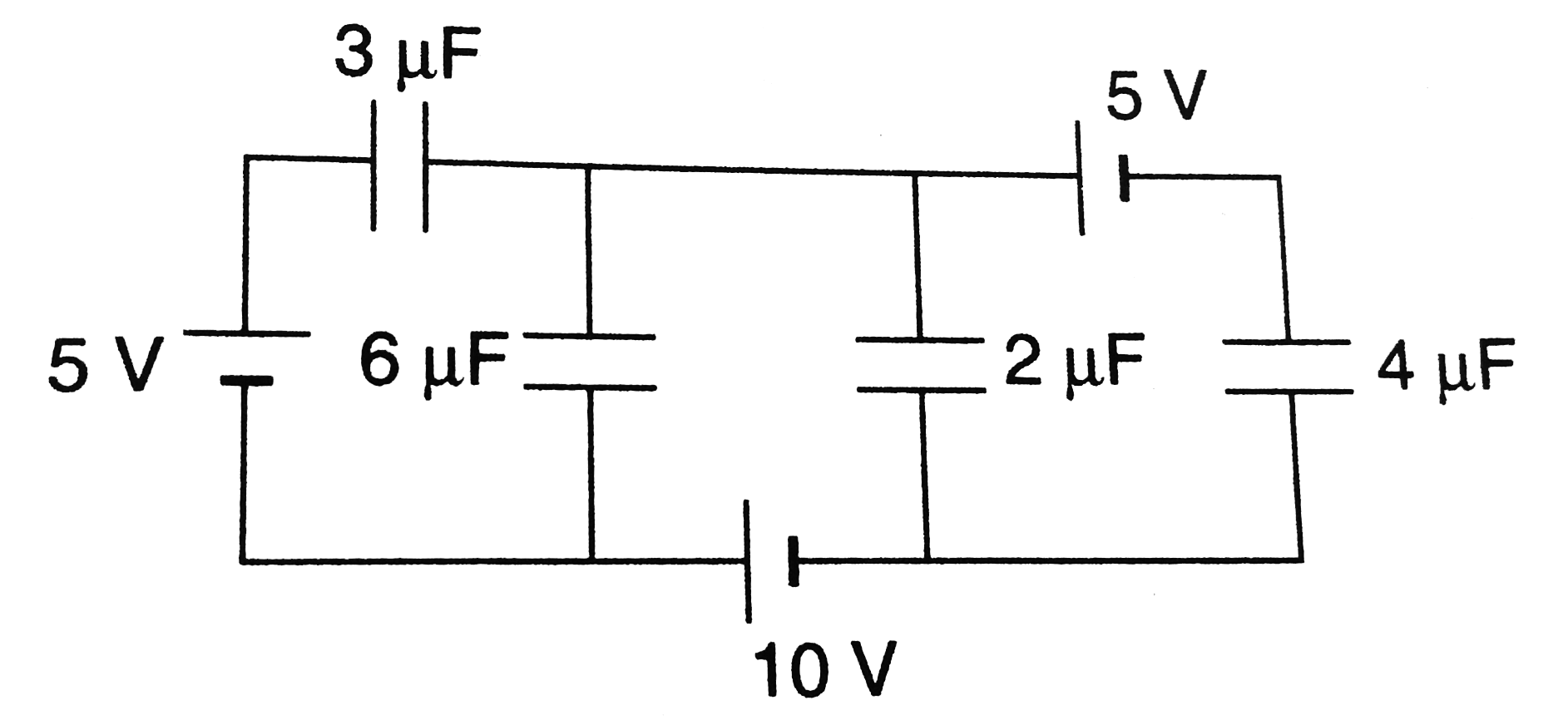 View Solution
View Solution


