Three long concentric conducting cylindrical shells have radii R, 2R and 2√2R Inner and outer shells are connected to each other. The capacitance across middle and inner shells per unit length is:
13∈0ln2
6π∈0ln2
π∈0ln2
None
The correct Answer is:B
To find the capacitance across the middle and inner cylindrical shells per unit length, we can follow these steps:
Step 1: Identify the Radii
We have three concentric cylindrical shells with the following radii:
- Inner shell (R1) = R
- Middle shell (R2) = 2R
- Outer shell (R3) = 2√2 R
Step 2: Use the Capacitance Formula for Cylindrical Capacitors
The capacitance C per unit length for a cylindrical capacitor is given by the formula:
C=2πϵ0ln(R2R1)
where R1 is the inner radius and R2 is the outer radius.
Step 3: Calculate Capacitance C1 between Inner and Middle Shells
For the capacitance C1 between the inner shell (R) and the middle shell (2R):
- R1=R
- R2=2R
Substituting these values into the formula:
C1=2πϵ0ln(2RR)=2πϵ0ln(2)
Step 4: Calculate Capacitance C2 between Middle and Outer Shells
For the capacitance C2 between the middle shell (2R) and the outer shell (2√2 R):
- R1=2R
- R2=2√2R
Substituting these values into the formula:
C2=2πϵ0ln(2√2R2R)=2πϵ0ln(√2)=2πϵ012ln(2)=4πϵ0ln(2)
Step 5: Combine the Capacitances
Since the capacitors C1 and C2 are in parallel, the total capacitance Ctotal is given by:
Ctotal=C1+C2
Substituting the values we calculated:
Ctotal=2πϵ0ln(2)+4πϵ0ln(2)=6πϵ0ln(2)
Final Answer
Thus, the capacitance across the middle and inner shells per unit length is:
Ctotal=6πϵ0ln(2)
---
We have three concentric cylindrical shells with the following radii:
- Inner shell (R1) = R
- Middle shell (R2) = 2R
- Outer shell (R3) = 2√2 R
The capacitance C per unit length for a cylindrical capacitor is given by the formula:
C=2πϵ0ln(R2R1)
where R1 is the inner radius and R2 is the outer radius.
For the capacitance C1 between the inner shell (R) and the middle shell (2R):
- R1=R
- R2=2R
C1=2πϵ0ln(2RR)=2πϵ0ln(2)
For the capacitance C2 between the middle shell (2R) and the outer shell (2√2 R):
- R1=2R
- R2=2√2R
C2=2πϵ0ln(2√2R2R)=2πϵ0ln(√2)=2πϵ012ln(2)=4πϵ0ln(2)
Since the capacitors C1 and C2 are in parallel, the total capacitance Ctotal is given by:
Ctotal=C1+C2
Substituting the values we calculated:
Ctotal=2πϵ0ln(2)+4πϵ0ln(2)=6πϵ0ln(2)
Thus, the capacitance across the middle and inner shells per unit length is:
Ctotal=6πϵ0ln(2)
Topper's Solved these Questions
- BOOK - AAKASH SERIESCHAPTER - CAPACITORS EXERCISE - PRACTICE SHEET (EXERCISE - I) (LEVEL - I (MAIN)) (Straight Objective Type Questions)9videos
CAPACITORS
- BOOK - AAKASH SERIESCHAPTER - CAPACITORS EXERCISE - PRACTICE SHEET (EXERCISE - I) (LEVEL - II (ADVANCED)) (Straight Objective Type Questions)4videos
CAPACITORS
- BOOK - AAKASH SERIESCHAPTER - CAPACITORS EXERCISE - LECTURE SHEET (EXERCISE - IV) (LEVEL - II (ADVANCED)) (Integer Type Questions )3videos
CAPACITORS
- BOOK - AAKASH SERIESCHAPTER - ATOMSEXERCISE - PRACTICE EXERCISE21videos
ATOMS
- BOOK - AAKASH SERIESCHAPTER - COMMUNICATION SYSTEM EXERCISE - LECTURE SHEET (LEVEL - I) (MAIN) (EXERCISE - IV) (Straight Objective & More than one Correct Answer Type Questions)20videos
COMMUNICATION SYSTEM
Similar Questions
There are two concentric conducting spherical shells of radii 10cm and 20cm. The outer shell is charged to a potential of 50esu while inner shell is earthed. The charge on outer shell is
View SolutionTwo concentric conducting shells of radii R and 2R are having charges Q and -2Q respectively.In a region r
View SolutionThree concentric conducting spherical shells have radii r, 2r, and 3r and charges q1,q2andq3, respectively. Innermost and outermost shells are earthed as shown in figure. The charges shown are after earthing. Select the correct alternative.
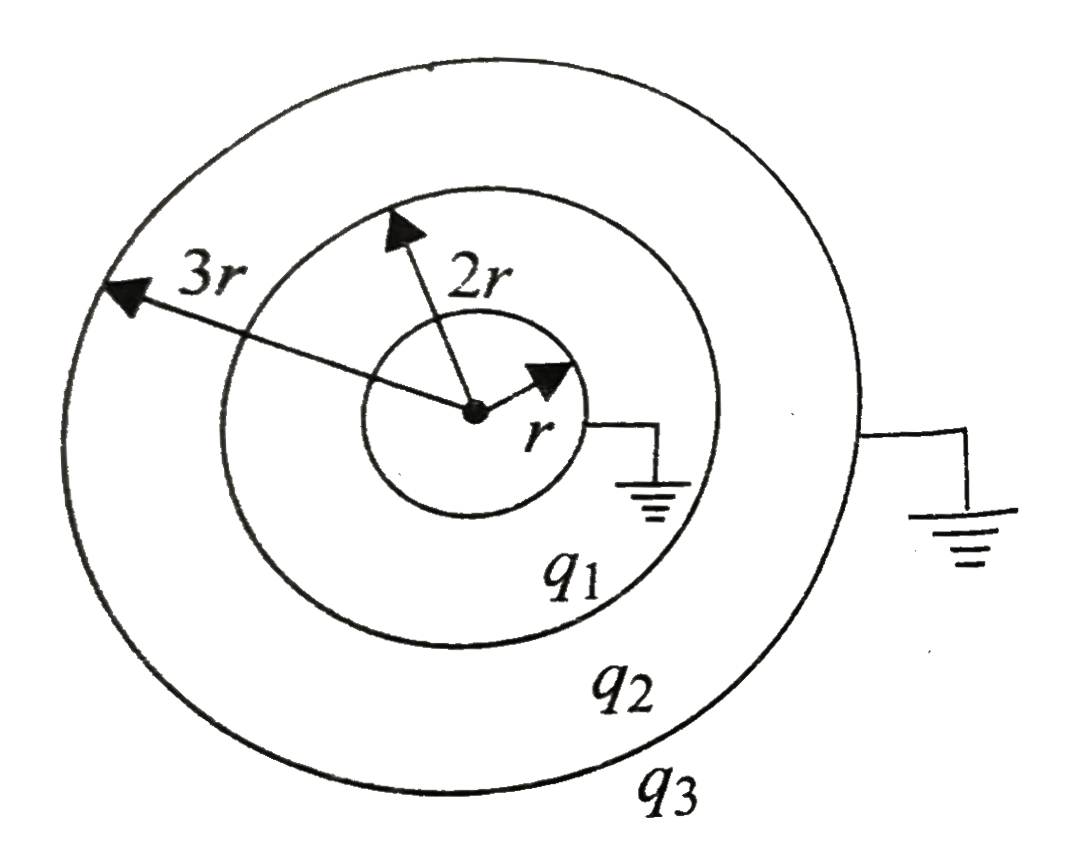 View Solution
View SolutionTwo concentric spherical conducting shells of radii r and R (r<R) carry charges q and Q respectively . The two shells are now connected by a conducting wire. The final charge on the inner shell is
View SolutionThree concentric conducting spherical shells of radii R, R2 and 3R carry charges Q,-2Q and 3Q, respectively compute the electric field at r=52R
 View Solution
View SolutionThere are two concentric conducting shells of radius R,2R respectively. Charge on each surface is as shown in the figure.

Equivalent capacitance of this system is:View Solutionthere are two concentric metallic shells of radii R and 2R, if outer shell is given charge q1 , then charge on surface of inner shell will be
View SolutionThree concentric conducting spherical shells carry charges as : +4Q on the inner shell, −2Q on the middle shell and −5Q on the outer shell. The charge on the inner surface of the outer shell is
View SolutionThree concentric conducting sphereical shells carry charges +4Q on the inner shell −2Q on the middle shel and +6Q on the outer shell. The charge on the inner surface of the outer shell is
View SolutionThere are two concentric hollow conducting spherical shells of radii r and R(R>r). The charge on the outer shell is Q. What charge should be given to the inner shell, so that the potential at a point P , at a distance 2R from the common centre is zero ?
View Solution
