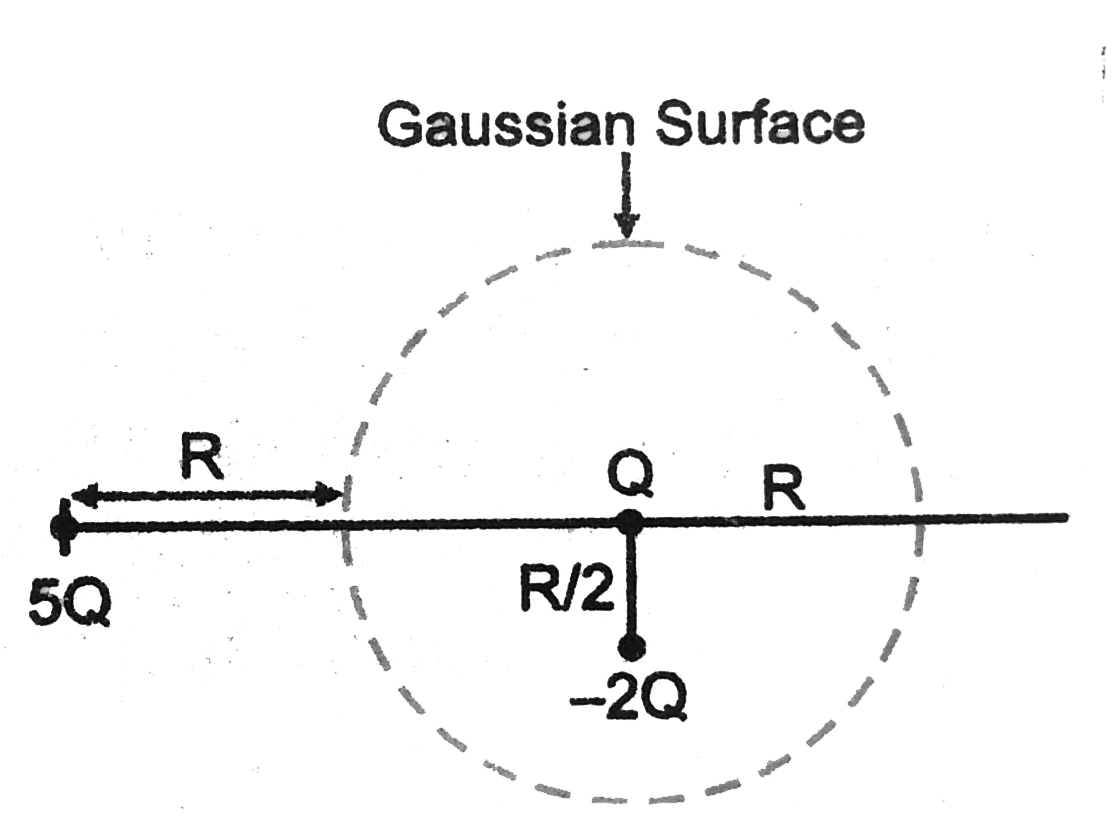
A positive charge .Q. is fixed at a point, A negatively charged of mass .m. and charge .q. is revolving in a circular path of radius radius r1 with .Q. as the centre. The change in potential energy to change the radius of the circular path from r1andr2 in joule is
zero
14π∈oQq[1r1−1r2]
1π∈oQq[1r1−1r2]
Qq4π∈o[1r2−1r1]
The correct Answer is:B
To solve the problem, we need to calculate the change in potential energy when the radius of the circular path of a negatively charged particle changes from r1 to r2 while revolving around a fixed positive charge Q.
1. Understanding the System:
- We have a positive charge Q fixed at a point.
- A negatively charged particle with charge q and mass m is revolving in a circular path of radius r1 around the charge Q.
2. Potential Energy Calculation:
- The potential energy U of a charge q in the electric field of another charge Q at a distance r is given by:
U=−kQqr
- Here, k is Coulomb's constant, k=14πϵ0.
3. Potential Energy at Radius r1:
- The potential energy U1 when the radius is r1:
U1=−kQqr1
4. Potential Energy at Radius r2:
- The potential energy U2 when the radius is r2:
U2=−kQqr2
5. Change in Potential Energy:
- The change in potential energy ΔU when the radius changes from r1 to r2 is given by:
ΔU=U2−U1
- Substituting the expressions for U1 and U2:
ΔU=(−kQqr2)−(−kQqr1)
- Simplifying this gives:
ΔU=−kQqr2+kQqr1=kQq(1r1−1r2)
6. Final Expression:
- Therefore, the change in potential energy when the radius changes from r1 to r2 is:
ΔU=kQq(1r1−1r2)
- We have a positive charge Q fixed at a point.
- A negatively charged particle with charge q and mass m is revolving in a circular path of radius r1 around the charge Q.
- The potential energy U of a charge q in the electric field of another charge Q at a distance r is given by:
U=−kQqr
- Here, k is Coulomb's constant, k=14πϵ0.
- The potential energy U1 when the radius is r1:
U1=−kQqr1
- The potential energy U2 when the radius is r2:
U2=−kQqr2
- The change in potential energy ΔU when the radius changes from r1 to r2 is given by:
ΔU=U2−U1
- Substituting the expressions for U1 and U2:
ΔU=(−kQqr2)−(−kQqr1)
- Simplifying this gives:
ΔU=−kQqr2+kQqr1=kQq(1r1−1r2)
- Therefore, the change in potential energy when the radius changes from r1 to r2 is:
ΔU=kQq(1r1−1r2)
Topper's Solved these Questions
- ELECTROSTATICSBOOK - AAKASH SERIESCHAPTER - ELECTROSTATICSEXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL -II LECTURE SHEET (ADVANCED) STRAIGHT OBJECTIVE TYPE QUESTIONS)
20 Videos
- ELECTROSTATICSBOOK - AAKASH SERIESCHAPTER - ELECTROSTATICSEXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL -II LECTURE SHEET (ADVANCED) MORE THAN ONE CORRECT ANSWER TYPE QUESTIONS)
4 Videos
- ELECTROSTATICSBOOK - AAKASH SERIESCHAPTER - ELECTROSTATICSEXERCISE - PRACTICE SHEET (EXERCISE -V ELECTRIC DIPOLE) (LEVEL -II INTEGER TYPE QUESTION)
2 Videos
- ELECTROMAGNETICSBOOK - AAKASH SERIESCHAPTER - ELECTROMAGNETICSEXERCISE - ADDITIONAL EXERCISE
13 Videos
- ELEMENTS OF VECTORSBOOK - AAKASH SERIESCHAPTER - ELEMENTS OF VECTORSEXERCISE - QUESTIONS FOR DESCRIPTIVE ANSWERS
10 Videos
Similar Questions
Knowledge Check
The work done in carrying a charge q once round a circle of radius r with a charge Q at the centre is
AqQ4πε0aBqQ4πε0a2Cq4πε0aDzero
A charged particle of mass m and charge q travels on a circular path of radius r that is perpendicular to a magnetic field B. The time takeen by the particle to complete one revolution is
View SolutionA particle of mass 'm' is moving on a circular path of radius 'r' with uniform speed 'v'. Rate of change of linear momentum is
View SolutionA particle of mass m carrying charge '+q1' is revolving around a fixed charge '−q2' in a circular path of radius r. Calculate the period of revolution.
View SolutionA particle having charge + q is fixed at a point O and a second particle of mass m and having charge −q0 moves with constant speed in a circle of radius r about the charge +q. the energy required to be supplied to the moving charge to increase radius of the path to 2r is qq0nπε0r. Find the value of n.
View Solution
A particle is moving on a circular path of radius r with uniform velocity v. The change in velocity when the particle moves from P to Q is (∠POQ=40∘)
View SolutionA charged particle of mass m and charge q describes circular motion of radius r in a uniform magnetic field of strength B the frequency of revolution is
View SolutionA particle of mass m having a charge q enters into a circular region of radius R with velocity v directed towards the centre. The strength of magnetic field is B. Find the deviation in the path of the particle.
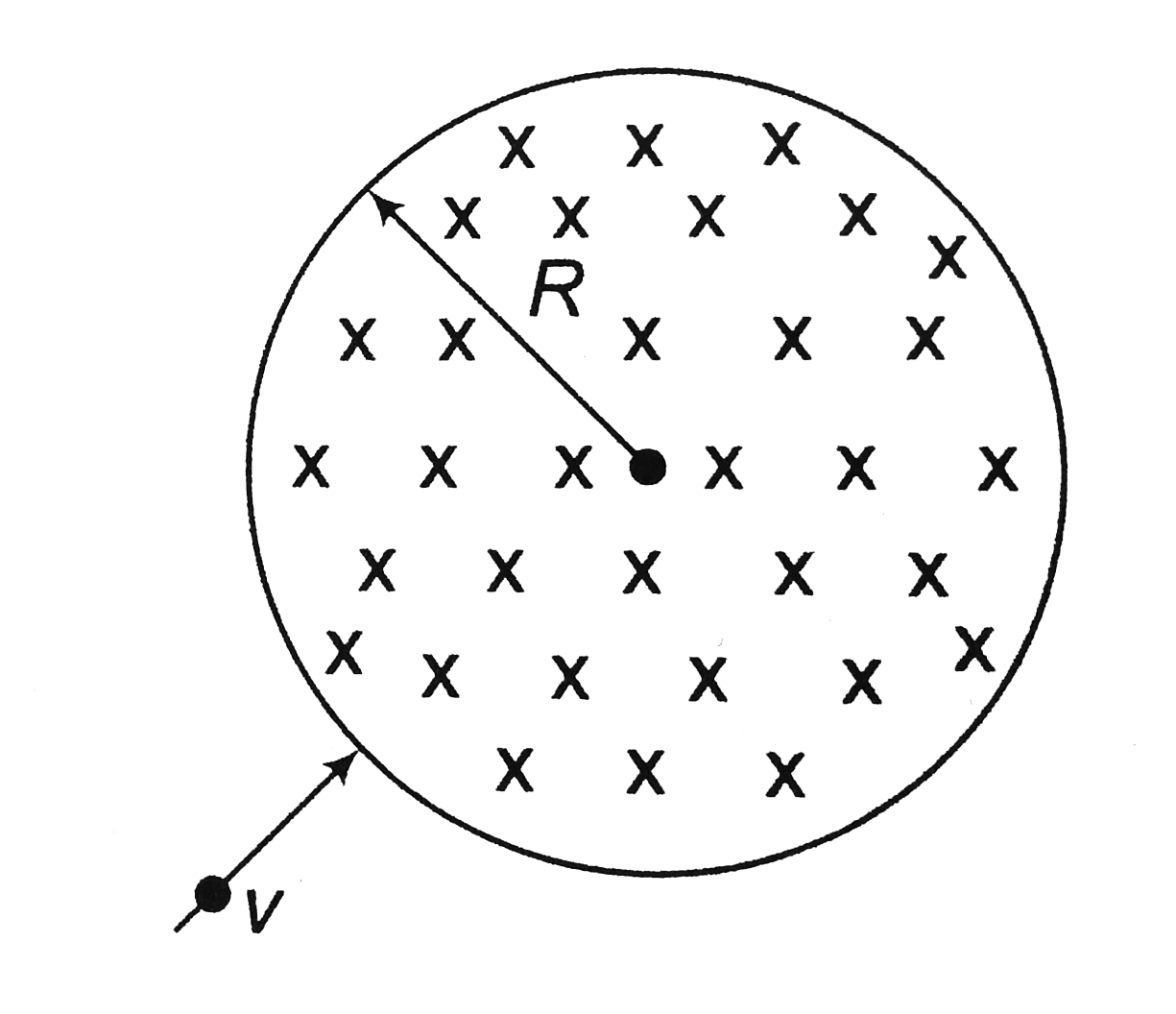
View Solution