A dipole of dipole moment P is kept at the centre of a ring of radius R and charge Q. If the dipole lies along the axis of the ring. Electric force on the ring due to the dipole is : (K=14πε0)
zero
KPQR3
2KPQR3
depends on the distribution of Q on the ring
The correct Answer is:B
To solve the problem of finding the electric force on a charged ring due to a dipole placed at its center, we can follow these steps:
1. Understanding the Setup:
- We have a dipole with a dipole moment P located at the center of a ring of radius R.
- The ring has a total charge Q uniformly distributed along its circumference.
2. Electric Field Due to the Dipole:
- The electric field E at a distance R from the dipole along its axis is given by the formula:
E=k⋅2PR3
where k=14πϵ0.
3. Force on the Ring:
- The electric force F on the ring due to the dipole can be calculated using the formula:
F=E⋅Q
- Substituting the expression for E:
F=(k⋅2PR3)⋅Q
4. Final Expression for the Force:
- Thus, the total electric force F on the ring due to the dipole is:
F=2kPQR3
Final Answer:
The electric force on the ring due to the dipole is:
F=2kPQR3
- We have a dipole with a dipole moment P located at the center of a ring of radius R.
- The ring has a total charge Q uniformly distributed along its circumference.
- The electric field E at a distance R from the dipole along its axis is given by the formula:
E=k⋅2PR3
where k=14πϵ0.
- The electric force F on the ring due to the dipole can be calculated using the formula:
F=E⋅Q
- Substituting the expression for E:
F=(k⋅2PR3)⋅Q
- Thus, the total electric force F on the ring due to the dipole is:
F=2kPQR3
The electric force on the ring due to the dipole is:
F=2kPQR3
Topper's Solved these Questions
- ELECTROSTATICSBOOK - AAKASH SERIESCHAPTER - ELECTROSTATICSEXERCISE - PRACTICE SHEET (EXERCISE -V ELECTRIC DIPOLE) (LEVEL -II LINKED COMPREHENSION TYPE QUESTION)
2 Videos
- ELECTROSTATICSBOOK - AAKASH SERIESCHAPTER - ELECTROSTATICSEXERCISE - PRACTICE SHEET (EXERCISE -V ELECTRIC DIPOLE) (LEVEL -II INTEGER TYPE QUESTION)
2 Videos
- ELECTROSTATICSBOOK - AAKASH SERIESCHAPTER - ELECTROSTATICSEXERCISE - PRACTICE SHEET (EXERCISE -V ELECTRIC DIPOLE) (LEVEL - I (MAIN) STRAIGHT OBJECTIVE TYPE QUESTIONS)
4 Videos
- ELECTROMAGNETICSBOOK - AAKASH SERIESCHAPTER - ELECTROMAGNETICSEXERCISE - ADDITIONAL EXERCISE
13 Videos
- ELEMENTS OF VECTORSBOOK - AAKASH SERIESCHAPTER - ELEMENTS OF VECTORSEXERCISE - QUESTIONS FOR DESCRIPTIVE ANSWERS
10 Videos
Similar Questions

Two point electric dipoles with dipole moment P1 and P2 are separated by a distance r with their dipole axes mutually perpendicular as shown. The force of interaction between the dipoles is (where k=14πε0)
View SolutionA short dipole of dipole moment P is placed near a point charge Q as shown in figure. Find force on the dipole due to the point charge

View SolutionA short dipole of dipole moment P is placed near a point charge Q as shown in figure. Find force on the dipole due to the point charge

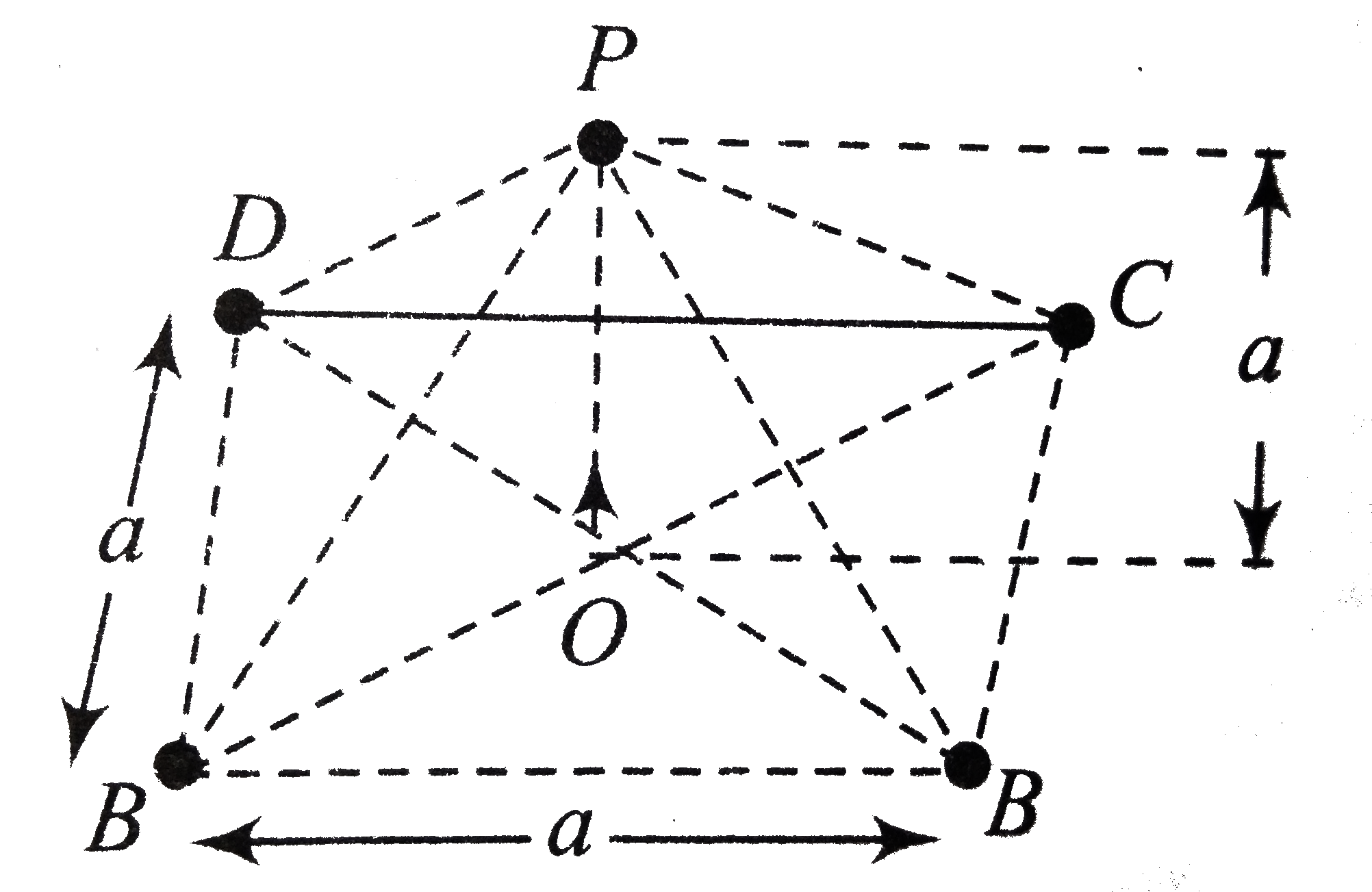
View SolutionFour charge particles each having charge Q=1 C are fixed at the corners of the base(A,B,C, and D) of a square pyramid with slant length a(AP=BP=PC=a=√2m), a charge -Q is fixed at point P. A dipole with dipole moment p=1 C-m is placed at the center of the bases and perpendicular to its plane as shown in fig. Force on the dipole due to the charge particles is □4πε0N.
View SolutionA short electric dipole is placed at a distance x from centre O on the axis of a ring of radius R and charge Q is uniformly distributed over tis.

The net force acting on the dipole will be
View SolutionA short electric dipole is placed at a distance x from centre O on the axis of a ring of radius R and charge Q is uniformly distributed over tis.

[(a) (find the net force acting on the dipole b) The work done external agent in rotating the dipole through 180∘ would be
View SolutionAn electric dipole is placed along x-axis with its centre at origin:
View SolutionCalculate potential on the axis of a ring due to charge Q uniformly distributed along the ring of radius R.
View SolutionElectric charge Q is uniformly distributed around a thin ring of radius a. find the potential a point P on the axis of the ring at a distance x from the centre of the ring .

View SolutionTwo equal charges q of opposite sign separated by a distance 2a constitute an electric dipole of dipole moment p. If P is a point at a distance r from the centre of the dipole and the line joining the centre of the dipole to this point makes an angle θ with the axis of the dipole, then then potential at P is given by (r>>2a) where (p = 2 qa)
View Solution
