Charges 5μC,−2μC,3μCand−9μC are placed at the corners A,B,C and D of a square ABCD of side 1m. The net electric potential at the centre of th square is
−27KV
−27√2KV
−90KV
zero
The correct Answer is:B
To find the net electric potential at the center of the square formed by the charges at its corners, we will follow these steps:
Step 1: Identify the charges and their positions
The charges are:
- At corner A: QA=5μC=5×10−6C
- At corner B: QB=−2μC=−2×10−6C
- At corner C: QC=3μC=3×10−6C
- At corner D: QD=−9μC=−9×10−6C
Step 2: Calculate the distance from the center to each corner
For a square with a side length of 1m, the distance from the center of the square to any corner (using the Pythagorean theorem) is:
d=√12+122=√22=1√2m
Step 3: Write the formula for electric potential
The electric potential V due to a point charge Q at a distance r is given by:
V=kQr
where k is Coulomb's constant, k=9×109N⋅m2/C2.
Step 4: Calculate the potential at the center due to each charge
The total potential at the center VO is the sum of the potentials due to each charge:
VO=VA+VB+VC+VD
Substituting the values:
VO=k⋅QAd+k⋅QBd+k⋅QCd+k⋅QDd
Factoring out k/d:
VO=kd(QA+QB+QC+QD)
Step 5: Substitute the values of the charges and distance
Substituting d=1√2:
VO=k√2(QA+QB+QC+QD)
Calculating the sum of the charges:
QA+QB+QC+QD=5×10−6−2×10−6+3×10−6−9×10−6=(5−2+3−9)×10−6=−3×10−6C
Step 6: Substitute the values into the potential formula
Now substituting back:
VO=k√2(−3×10−6)
VO=9×109⋅√2⋅(−3×10−6)
Calculating:
VO=−27√2×103V
Final Answer
The net electric potential at the center of the square is:
VO=−27√2×103V
The charges are:
- At corner A: QA=5μC=5×10−6C
- At corner B: QB=−2μC=−2×10−6C
- At corner C: QC=3μC=3×10−6C
- At corner D: QD=−9μC=−9×10−6C
For a square with a side length of 1m, the distance from the center of the square to any corner (using the Pythagorean theorem) is:
d=√12+122=√22=1√2m
The electric potential V due to a point charge Q at a distance r is given by:
V=kQr
where k is Coulomb's constant, k=9×109N⋅m2/C2.
The total potential at the center VO is the sum of the potentials due to each charge:
VO=VA+VB+VC+VD
Substituting the values:
VO=k⋅QAd+k⋅QBd+k⋅QCd+k⋅QDd
Factoring out k/d:
VO=kd(QA+QB+QC+QD)
Substituting d=1√2:
VO=k√2(QA+QB+QC+QD)
Calculating the sum of the charges:
QA+QB+QC+QD=5×10−6−2×10−6+3×10−6−9×10−6=(5−2+3−9)×10−6=−3×10−6C
Now substituting back:
VO=k√2(−3×10−6)
VO=9×109⋅√2⋅(−3×10−6)
Calculating:
VO=−27√2×103V
The net electric potential at the center of the square is:
VO=−27√2×103V
Topper's Solved these Questions
- ELECTROSTATICSBOOK - AAKASH SERIESCHAPTER - ELECTROSTATICSEXERCISE - PRACTICE SHEET (EXERCISE -IV ELECTRIC POTENTIAL & POTENTIAL ENERGY) (LEVEL - II (ADVANCED) STRAIGHT OBJECTIVE TYPE QUESTION)
28 Videos
- ELECTROSTATICSBOOK - AAKASH SERIESCHAPTER - ELECTROSTATICSEXERCISE - PRACTICE SHEET (EXERCISE -IV ELECTRIC POTENTIAL & POTENTIAL ENERGY) (LEVEL - II (ADVANCED) MORE THAN ONE CORRECT ANSWER TYPE QUESTION)
1 Videos
- ELECTROSTATICSBOOK - AAKASH SERIESCHAPTER - ELECTROSTATICSEXERCISE - PRACTICE SHEET (EXERCISE -III ELECTRO FLUX & GAUSS.S LAW) (LEVEL - I (MAIN) INTEGER TYPE QUESTIONS
2 Videos
- ELECTROMAGNETICSBOOK - AAKASH SERIESCHAPTER - ELECTROMAGNETICSEXERCISE - ADDITIONAL EXERCISE
13 Videos
- ELEMENTS OF VECTORSBOOK - AAKASH SERIESCHAPTER - ELEMENTS OF VECTORSEXERCISE - QUESTIONS FOR DESCRIPTIVE ANSWERS
10 Videos
Similar Questions
Knowledge Check
Four particles each of mass m are placed at the vertices of a square of side l. the potential at the centre of square is
A−√2Gm2l(2−1√2)B−2Gm2l(2+1√2)C−√2Gm2l(√2−1√2)D−2Gm2l(√2−1√2)
Charges q,2q,3q and 4q are placed at the corners A,B,C and D of a square as shown in the following figure. The directon of electric field at the centre of the square is along
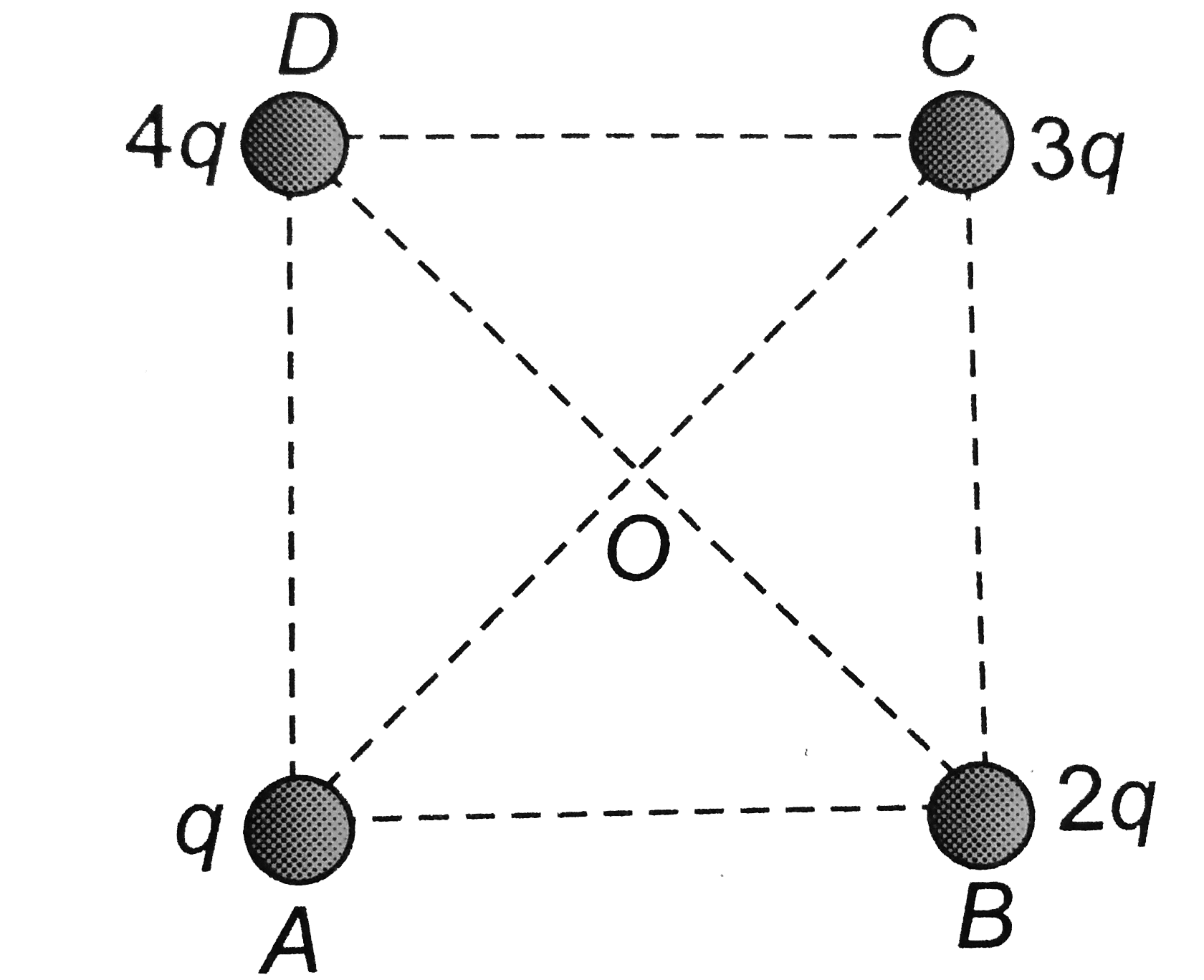
View SolutionCharges q,2q,3q and 4q are placed at the corners A,B,C and D of a square as shown in the following figure. The directon of electric field at the centre of the square is along

View SolutionFour point charges are placed at the corners of a square of side l. Calculate potential at the centre of square.
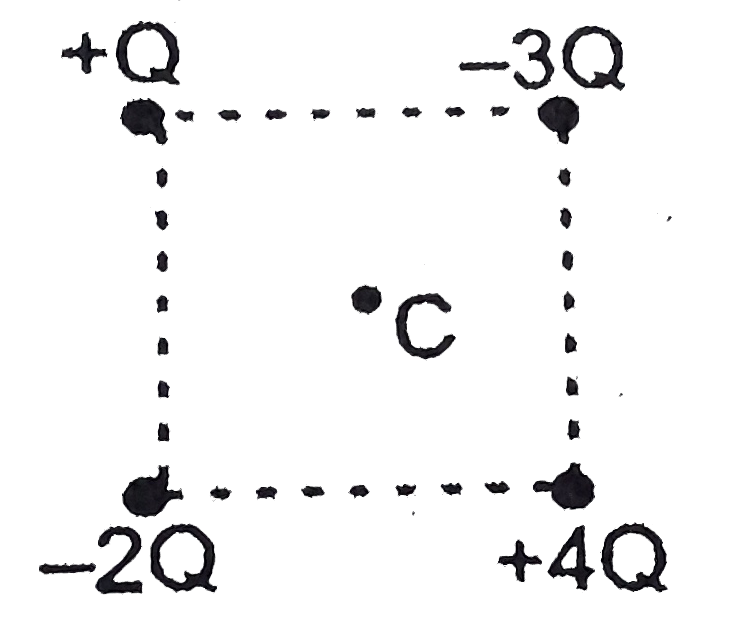
View SolutionFour charges of same magnitude q are placed at four corners of a square of side a . The value electric potential at the centre of the souare will be (where k = 14πε0 )
View SolutionFour charges of +q, +q +q and +q are placed at the corners A, B, C and D of s square. The resultant force on the charge at D
View SolutionFour charges of 6μC,2μC,−12μCand4μC are placed at the corners of a square of side 1m. The square is in x-y plane and its centre is at origin. Electric potential due to these charges is zero everywhere or the line
View SolutionFour point charges are placed at the corners of a square ABCD of side 10 cm, as shown in figure. The force on a charge of 1μC placed at the centre of square is
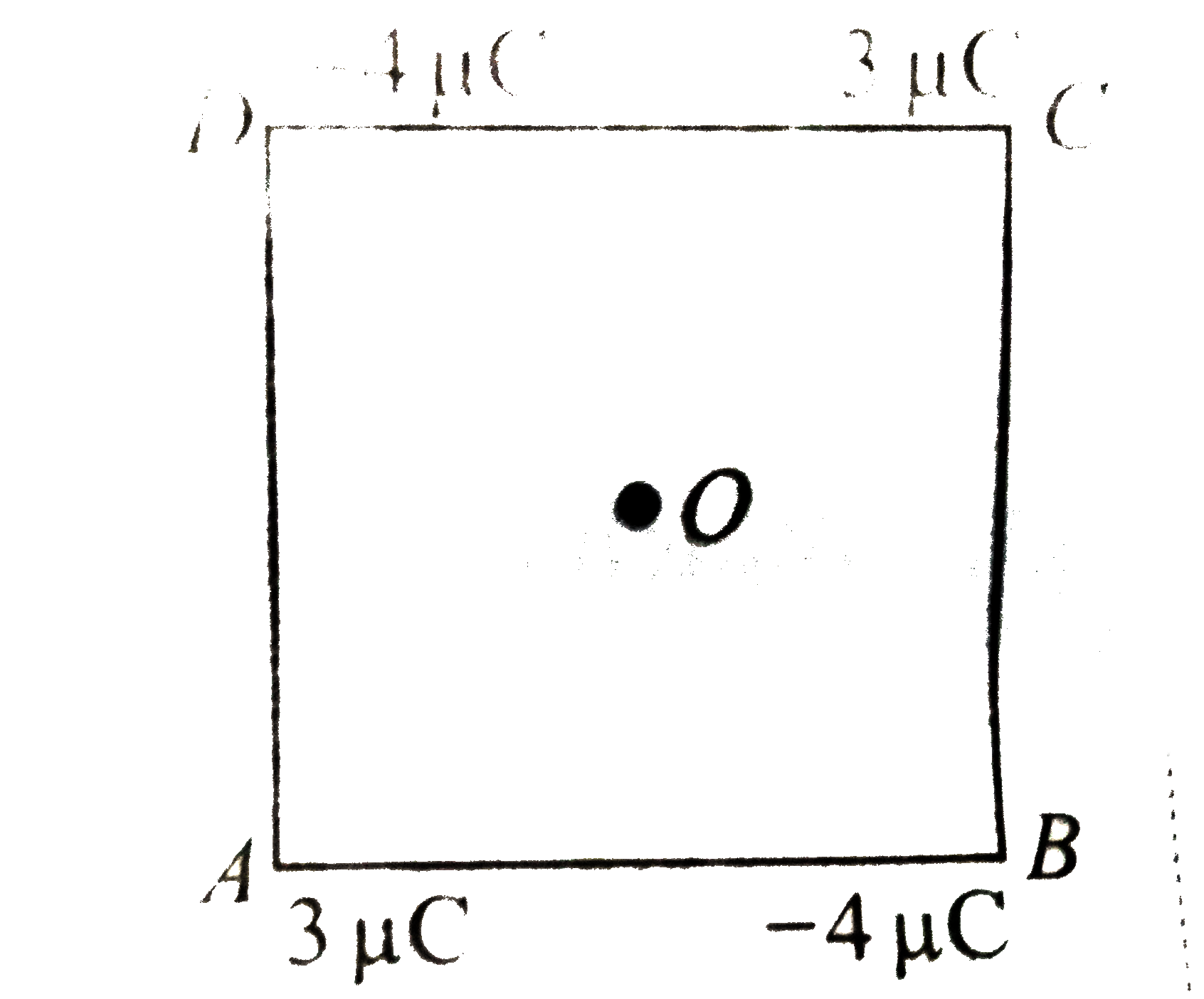
View Solution
