The magnetic energy stored in a long solenoid of area of cross-section A in a small region of length L is
B2AL2μ20
AL2μ0
12μ0B2AL
B2AL2μ0
The correct Answer is:D
To find the magnetic energy stored in a long solenoid of cross-sectional area A and length L, we can follow these steps:
Step 1: Understand the formula for energy density
The energy density u (energy per unit volume) stored in a magnetic field is given by the formula:
u=B22μ0
where B is the magnetic field strength and μ0 is the permeability of free space.
Step 2: Calculate the volume of the solenoid
The volume V of the small region of the solenoid can be calculated using the formula:
V=A×L
where A is the cross-sectional area and L is the length of the solenoid.
Step 3: Calculate the total magnetic energy stored
The total magnetic energy U stored in the solenoid can be calculated by multiplying the energy density by the volume:
U=u×V
Substituting the expressions for u and V:
U=(B22μ0)×(A×L)
Step 4: Simplify the expression
Now, substituting the volume into the equation:
U=B22μ0×(A×L)=B2AL2μ0
Final Answer
Thus, the magnetic energy stored in a long solenoid of cross-sectional area A in a small region of length L is given by:
U=B2AL2μ0
The energy density u (energy per unit volume) stored in a magnetic field is given by the formula:
u=B22μ0
where B is the magnetic field strength and μ0 is the permeability of free space.
The volume V of the small region of the solenoid can be calculated using the formula:
V=A×L
where A is the cross-sectional area and L is the length of the solenoid.
The total magnetic energy U stored in the solenoid can be calculated by multiplying the energy density by the volume:
U=u×V
Substituting the expressions for u and V:
U=(B22μ0)×(A×L)
Now, substituting the volume into the equation:
U=B22μ0×(A×L)=B2AL2μ0
Thus, the magnetic energy stored in a long solenoid of cross-sectional area A in a small region of length L is given by:
U=B2AL2μ0
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - AAKASH SERIESCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - EXERCISE-IB
18 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - AAKASH SERIESCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - EXERCISE-II
32 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - AAKASH SERIESCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Additional Exercise
11 Videos
- ELECTRIC FIELD AND POTENTIALBOOK - AAKASH SERIESCHAPTER - ELECTRIC FIELD AND POTENTIALEXERCISE - PROBLEMS (LEVEL-II)
26 Videos
- ELECTROMAGNETIC WAVESBOOK - AAKASH SERIESCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - EXERCISE -II
22 Videos
Similar Questions
(a) Obtain the expression for the magnetic energy stored in a solenoid in terms of magnetic field B, area A and length l of the solenoid. (b) How does this magnetic energy compare with the electrostatic energy stored in a capacitor?
View SolutionDerive the expression for the magnetic energy stored in a solenoid in terms of magnetic field B, area A and length l of the solenoid carrying a steady current 1. How does this magnetic energy per unit volume compare with the electrostatic energy density stored in a parallel plate capacitor ?
View SolutionThe self inductance of a solenoid of length L, area of cross-section A and having N turns is-
View SolutionAssertion : The self-inductionce of a long solenoid is proportional to the area of corss-section and length of the solenoid.
Reason : Self inductance of a solenoid is independent of the number of truns per unit length.
View SolutionThe magnetic field within a long, straight solenoid with a circular cross - section of radius r is (as shown) increasing at a rate of α.
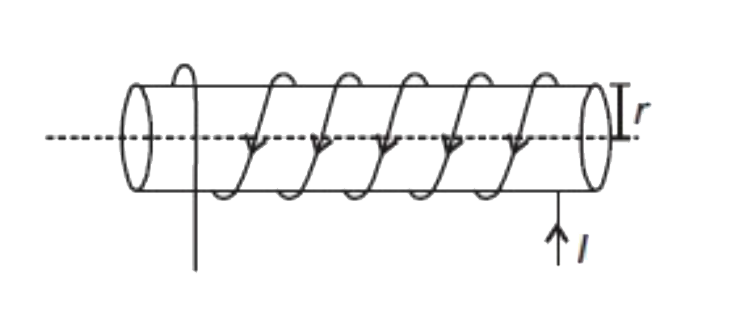
The rate of change of flux through a circle with radius a inside the solenoid and with centre on the solenoid axis is
View SolutionThe self inductance L of a solenoid of length l and area of cross-section A, with a fixed number of turns N increases as
View SolutionThe self inductance L of a solenoid of length l and area of cross-section A, with a fixed number of turns N increases as
View SolutionThe self inductance L of a solenoid of length l and area of cross-section A, with a fixed number of turns N increases as
View SolutionA thin wire ring of radius a and resitance r is located inside a long solenoid is equal to l, its cross-sectional radius , to b. At a certain moment the solenoid was connected to a source of a constant voltage V. The total resistance of the circuit is equal to R. Assuming the the radial force acting per unit length of the ring.
View SolutionConsidering a wire of non-uniform cross-section as shown.If the area of cross-section at A is double of the area of cross-section at point B.Ratio of heat energy dissipated in a unit volume per unit time at points A and B is
_PHY_E05_279_Q01.png)
View Solution
