A conducting rod OA of length l is rotated about its end O with an angular velocity in a uniform magnetic field directed perpendicualr to the rotation. Find the emf induced in the rod, between it's ends.
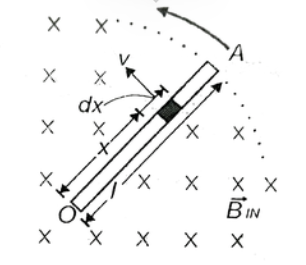
The magnetic field induction due to current i is different at different sections of the rod, because they are at different distances from the wire.
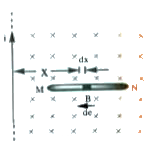
Let us, first of all, subdivide the entire length of the conductor MN into elementary sections. Consider a section (shown shaded in the figure (b)) of thickness dx at a distance x from the wire. As all the three, v, B and (dX) are mutually normally to each other, so the emf induced in it is de = Bvdx. (from N to M by Fleming.s right hand rule)
For the rest of sections, the induced emf is in the same sense, (i.e, from N to M)
Total emf induced in the conductor is
. Substituting for , the above equation gets changed to
or
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBook:AAKASH SERIESChapter:ELECTROMAGNETIC INDUCTIONExercise:EXERCISE-IA
Explore 58 Videos
- ELECTROMAGNETIC INDUCTIONBook:AAKASH SERIESChapter:ELECTROMAGNETIC INDUCTIONExercise:EXERCISE-IB
Explore 18 Videos
- ELECTRIC FIELD AND POTENTIALBook:AAKASH SERIESChapter:ELECTRIC FIELD AND POTENTIALExercise:PROBLEMS (LEVEL-II)
Explore 26 Videos
- ELECTROMAGNETIC WAVESBook:AAKASH SERIESChapter:ELECTROMAGNETIC WAVESExercise:EXERCISE -II
Explore 22 Videos
Similar Questions
A conducting rod AB of length l is rotated about point O with an angular velocity velocity omega in a uniform magnetic field (B_0) directed perpendicular into the plane of rotation as shown in the figure. The value of VB−VA is
View SolutionA conducting rod of length l is rotating with constant angular velocity ω about point O in a uniform magnetic field B as shown in the figure . What is the emf induced between ends P and Q ?

View SolutionA metal rod length l rotates about on end with a uniform angular velocity ω. A uniform magnetic field →B exists in the direction of the axis of rotation. Calculate the emf induced between the ends of the rod. Neglect the centripetal force acting on the free electrons as they moving in circular paths.
View SolutionA conducting rod AC of length 4l is rotate about a point O in a uniform magnetic field →B directed into the paper. AO=l and OC=3l. Then
View SolutionA conducting rod of length 2l is rotating with constant angular speed w about its perpendicular bisector. A uniform magnetic field B exists parallel to the axis of rotation. The e.m.f. induced between two ends of the rod is
View SolutionA conducting rod of length 2l is rotating with constant angular speed w about its perpendicular bisector. A uniform magnetic field B exists parallel to the axis of rotation. The e.m.f. induced between two ends of the rod is

View SolutionA conducting circular loop of radius r is rotated about its diameter at a constant angular velocity ω in a magnetic field B perpendicular to the axis of rotation. In what position of the loop is the induced emf zero?
View Solution
A rod of mass 2 kg ad length 2 m is rotating about its one end O with an angular velocity ω=4rad/s. Find angular momentum of the rod about the axis rotation.
View SolutionA conducting disc of radius r rotaes with a small but constant angular velocity ω about its axis. A uniform magnetic field B exists parallel to the axis of rotation. Find the motional emf between the centre and the periphery of the disc.
View SolutionA square loop of side a is rotating about its diagonal with angular velocity ω in a perpendicular magnetic field →B It has 10 turns. The emf induced is
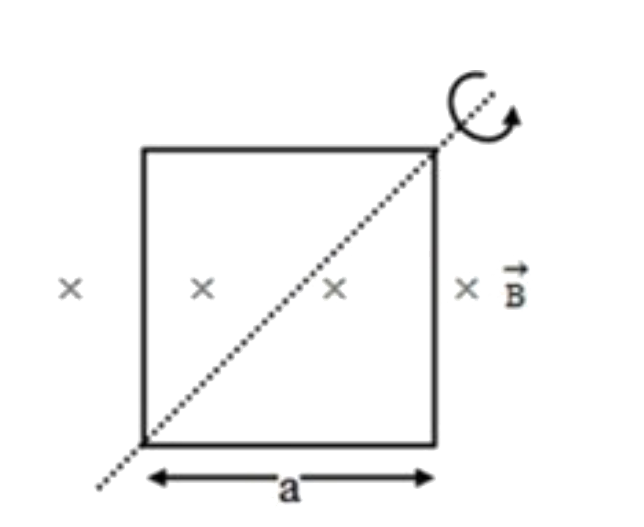
View Solution

