List-I List-II
a) interference e) transverse nature of light
b) diffraction f) unequal absorption of ordinary and extraordinary ray
c) polarization g) bands of equal width
d) dichroism h) bands of unequal width
A−F,B−G,C−H,D−E
A−H,B−G,C−F,D−E
A−E,B−F,C−G,D−H
A−G,B−H,C−E,D−F
The correct Answer is:D
To solve the problem of matching the items in List-I with those in List-II, we will analyze each term in List-I and find its corresponding match in List-II based on the principles of wave optics.
1. Interference (a):
- Interference refers to the phenomenon where two or more waves superpose to form a resultant wave. In this case, the result is characterized by bands of equal width, known as fringe width.
- Match: G (bands of equal width).
2. Diffraction (b):
- Diffraction is the bending of waves around obstacles and the spreading of waves when they pass through small openings. The resulting pattern typically shows bands of unequal width due to the varying intensity of light.
- Match: H (bands of unequal width).
3. Polarization (c):
- Polarization is the process by which the vibrations of light waves are restricted to a particular direction. This phenomenon is indicative of the transverse nature of light waves.
- Match: E (transverse nature of light).
4. Dichroism (d):
- Dichroism refers to the phenomenon where a material exhibits different colors when viewed from different angles or when different polarizations of light pass through it. This effect arises from the unequal absorption of ordinary and extraordinary rays.
- Match: F (unequal absorption of ordinary and extraordinary ray).
Final Matches:
- a) Interference → G (bands of equal width)
- b) Diffraction → H (bands of unequal width)
- c) Polarization → E (transverse nature of light)
- d) Dichroism → F (unequal absorption of ordinary and extraordinary ray)
Summary of Matches:
- A → G
- B → H
- C → E
- D → F
- Interference refers to the phenomenon where two or more waves superpose to form a resultant wave. In this case, the result is characterized by bands of equal width, known as fringe width.
- Match: G (bands of equal width).
- Diffraction is the bending of waves around obstacles and the spreading of waves when they pass through small openings. The resulting pattern typically shows bands of unequal width due to the varying intensity of light.
- Match: H (bands of unequal width).
- Polarization is the process by which the vibrations of light waves are restricted to a particular direction. This phenomenon is indicative of the transverse nature of light waves.
- Match: E (transverse nature of light).
- Dichroism refers to the phenomenon where a material exhibits different colors when viewed from different angles or when different polarizations of light pass through it. This effect arises from the unequal absorption of ordinary and extraordinary rays.
- Match: F (unequal absorption of ordinary and extraordinary ray).
- a) Interference → G (bands of equal width)
- b) Diffraction → H (bands of unequal width)
- c) Polarization → E (transverse nature of light)
- d) Dichroism → F (unequal absorption of ordinary and extraordinary ray)
- A → G
- B → H
- C → E
- D → F
Topper's Solved these Questions
- WAVES OPTICSBook:AAKASH SERIESChapter:WAVES OPTICSExercise:EXERCISE -IA (ASCENDING AND DSCENDING ORDER TYPE QUESTIONS)
Explore 6 Videos
- WAVES OPTICSBook:AAKASH SERIESChapter:WAVES OPTICSExercise:EXERCISE -IB (ASSERTION AND REASON)
Explore 67 Videos
- WAVES OPTICSBook:AAKASH SERIESChapter:WAVES OPTICSExercise:EXERCISE -IA (MORE THAN ONE OPTION)
Explore 14 Videos
- WAVESBook:AAKASH SERIESChapter:WAVESExercise:EXERCISE-III (Doppler effect :)
Explore 15 Videos
Similar Questions
List-I List-II
a) Einstein e) velocity of light
b) Huygen f) diffraction of light
c) Focault g) wave nature of light
d) Fresnel h) particle nature of light
View SolutionList-I List-II
a) Fresnel's diffraction e) Bright band
b) Fraunhofer's diffraction f) Source and screen are at finite distance
c) In interference phase difference is even multiple of π g) Dark band
d) In interference phase difference is odd multiple of π h) Source and screen are at infinite distance
View SolutionWhich of the following properties show that light is a transverse wave? a) Reflection b) Interference c) Diffraction d) Polarization
View SolutionA glass sheet 12×10−3 mm thick (μg=1.5) is placed in the path of one of the interfering beams in a Yongs's double slit interference arrangement using monochromatic light of wavelenght 6000 A. If the central bright fringe shifts a distance equal to width of 10 bands. What is the thickness of the sheet of diamond of refractive index 2.5 that has to be introduced in the path of second beam to bring th ecentral bright fringe to original position?
View SolutionList-I List-II
a) interference e) transverse nature of light
b) diffraction f) unequal absorption of ordinary and extraordinary ray
c) polarization g) bands of equal width
d) dichroism h) bands of unequal width
View SolutionMatch List-I with List-II

View SolutionOne mole of a monatomic ideal gas is taken along two cyclic processes E→F→G→EandE→F→H→E as shown in the PV diagram. The processes involved are purely isochoric , isobaric , isothermal or adiabatic .
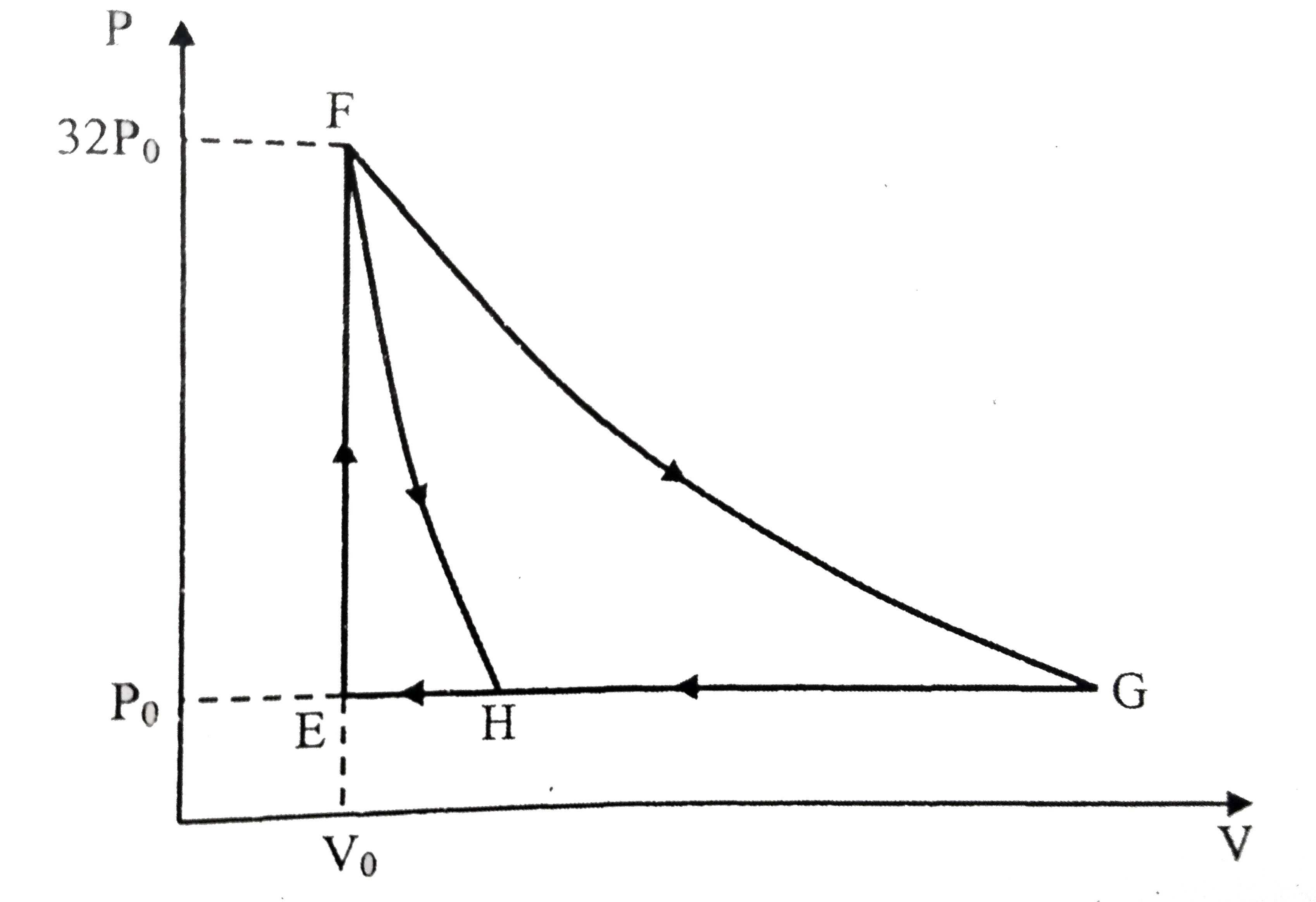
Match the paths in List I with the magnitudes of the work done in List II and select the correct answer using the codes given below the lists.

View Solution(a) (i) What is meant by diffraction of light?
(ii) In Fraunhofer diffraction, what kind of source of light is used and where is it situated ?
(b) Obtain the relation, dsinθ=λ for the first minima of the diffraction pattern of a single slit of width d using light of wavelength λ.
View SolutionList - I List -II
a) spherical wave front e) location of new wave front
b) plane wave front f) line source
c) cylindrical wave front g) point source at finite distance
d) Huygen's principle h) point source at infinite distance
View SolutionUse the given figure to express :
(i) a in terms of b and f,
(ii) e in terms of f and g,
(iii) d in terms of a and e,
(iv) c in terms of e and g.
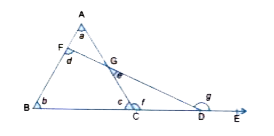
View Solution

