The angle between (¯¯¯Aׯ¯¯B)and(¯¯¯Bׯ¯¯A) is (in radiant)
π/2
π
π/4
zero
The correct Answer is:B
To find the angle between the vectors ¯AׯB and ¯BׯA, we can follow these steps:
Step 1: Understand the Cross Product Properties
The cross product of two vectors ¯A and ¯B is defined as:
¯AׯB=|¯A||¯B|sin(θ)^n
where θ is the angle between ¯A and ¯B, and ^n is the unit vector perpendicular to the plane formed by ¯A and ¯B.
Step 2: Apply the Anti-parallel Property
We know from the properties of the cross product that:
¯BׯA=−(¯AׯB)
This means that the vector ¯BׯA is in the opposite direction to ¯AׯB.
Step 3: Determine the Angle Between the Two Vectors
Since ¯AׯB and ¯BׯA are in opposite directions, they are considered anti-parallel. The angle ϕ between two anti-parallel vectors is:
ϕ=π radians(180∘)
Conclusion
Thus, the angle between ¯AׯB and ¯BׯA is:
ϕ=π radians
---
The cross product of two vectors ¯A and ¯B is defined as:
¯AׯB=|¯A||¯B|sin(θ)^n
where θ is the angle between ¯A and ¯B, and ^n is the unit vector perpendicular to the plane formed by ¯A and ¯B.
We know from the properties of the cross product that:
¯BׯA=−(¯AׯB)
This means that the vector ¯BׯA is in the opposite direction to ¯AׯB.
Since ¯AׯB and ¯BׯA are in opposite directions, they are considered anti-parallel. The angle ϕ between two anti-parallel vectors is:
ϕ=π radians(180∘)
Thus, the angle between ¯AׯB and ¯BׯA is:
ϕ=π radians
Similar Questions
The difference between ¯¯¯Cpand¯¯¯Cv is [¯¯¯Cpand¯¯¯Cv signify molar quantities ]
View Solution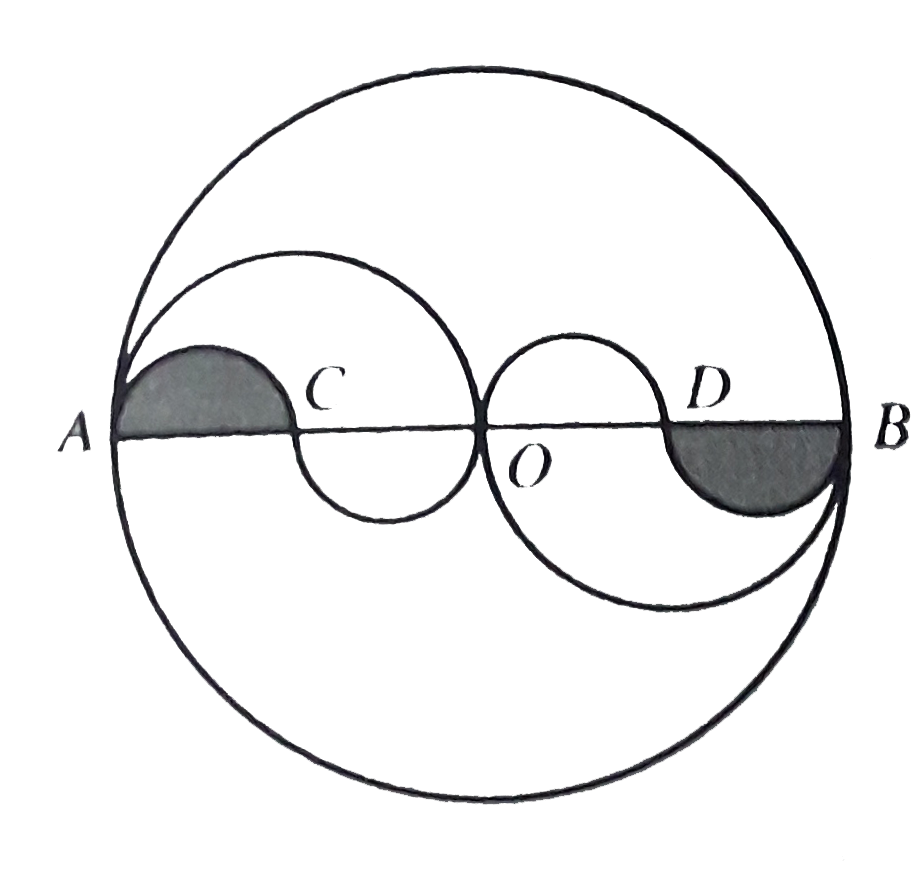
In the circle shown above, O is the center and ¯¯¯¯¯¯AB is a diameter . There are two semicircles with diameters ¯¯¯¯¯¯AO and ¯¯¯¯¯¯BO , and four smaller semicircles with congruent diameters ¯¯¯¯¯¯AC,¯¯¯¯¯¯CO,¯¯¯¯¯¯OD and ¯¯¯¯¯¯DB . A point is picked at random in the large circle . What is the probability that it lands in a shaded region ?
View Solution
Knowledge Check
Parallelogram ABCD is graphed in the standard (x,y) coordinate plane below. Sides ¯¯¯¯¯¯ABand¯¯¯¯¯¯CD are each √10 coordinate units long. Sides ¯¯¯¯¯¯ADand¯¯¯¯¯¯BC are each 5 coordinate unit long. The distance between ¯¯¯¯¯¯ADand¯¯¯¯¯¯BC is 3 coordinate units.
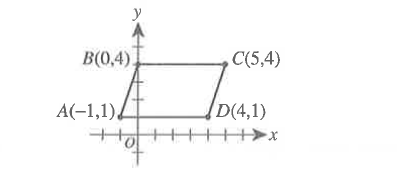
What is the distance, in coordinate units, from B to D?A3B4C5D7In the figure below , the circle with circle with center O is tangent to ¯¯¯¯¯¯AE,¯¯¯¯¯¯BD,and¯¯¯¯¯¯DE . The measure of angle ∠BDE is 75∘ and the maeasure of ∠DEA is 105∘
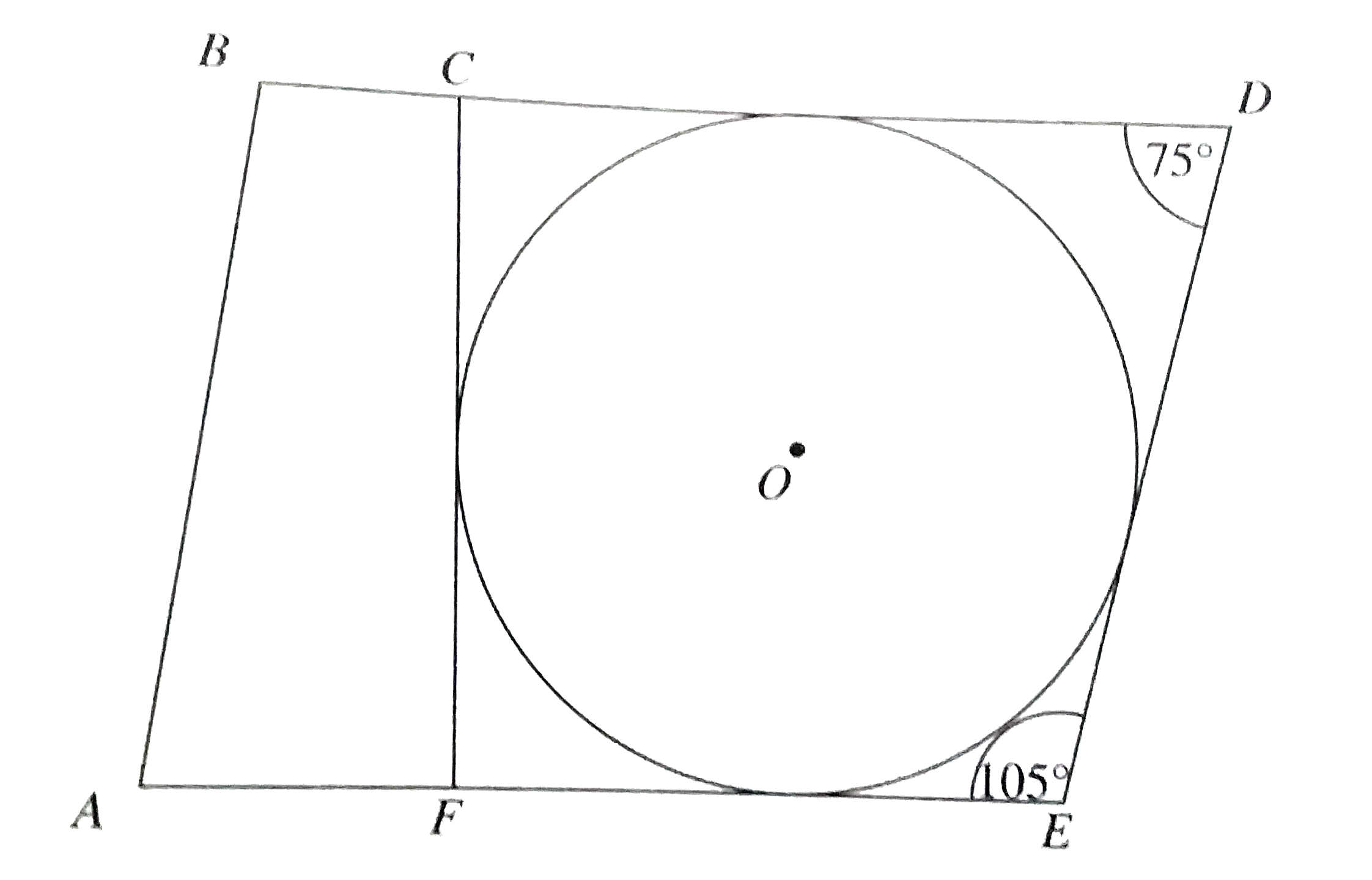
THe lines in which of the following pairs of lines are necessarily parallel ?
I.¯¯¯¯¯¯ABand¯¯¯¯¯¯DE
II.¯¯¯¯¯¯BDand¯¯¯¯¯¯AE
III.¯¯¯¯¯¯CFand¯¯¯¯¯¯DEAI onlyBII onlyCIII onlyDI and II onlyIn the figure shown below, E and G lie on ¯¯¯¯¯¯AC, D and F lie on ¯¯¯¯¯¯AB,¯¯¯¯¯¯DEand¯¯¯¯¯¯FG are parallel to ¯¯¯¯¯¯BC, and the given lengths are in feet. What is the length of ¯¯¯¯¯¯AC, in feet?
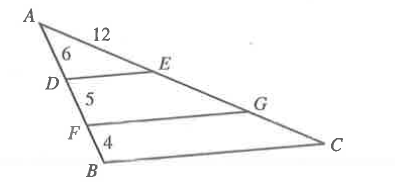 A9B18C21D30
A9B18C21D30
A : The poynting vector given as ¯¯¯S=¯¯¯Eׯ¯¯Bμ0 represents the instantaneous intensity at a point.
R : The velocity of an electromagnetic wave is in the direction of the vector ¯¯¯Eׯ¯¯B.
View Solution
In the figure shown above, ∠Q measures 70∘ , ¯¯¯¯¯¯PQ≅¯¯¯¯¯¯PR , and ¯¯¯¯¯¯PQ and ¯¯¯¯¯¯PR are tangent to the circle with center O at points A and B . Find , in degrees , the measure of ∠AOB.
View SolutionIn the Boolean algebra ¯¯¯A.¯¯¯B equals
View SolutionThe resultant of the three vectors ¯¯¯¯¯¯OA,¯¯¯¯¯¯OB and ¯¯¯¯¯¯OC shown in figure :-
View SolutionIn the figure shown below ,¯¯¯¯¯¯BC and bar(EF)areparal≤landbar(AE ) = bar(FD ) . ifangle ABC is130 ^(@) and angle (BAE)is22^@,wˆisthemeasureofangle (AEF) ?

View Solution
