(A) : Stationary bomb explodes into two fragments. They move with different velocities in oppsite directions.
(R ) : Explosion does not violate the low of conservation of linear momentum.
Both (A) and (R ) are true and (R ) is the correct explanation of (A)
Both (A) and (R ) are true and (R ) is not the correct explanation of (A)
(A) is true but (R ) is false
Both (A) and (R ) are false
The correct Answer is:A
To solve the question, we need to analyze the assertion and reason provided regarding the explosion of a stationary bomb and the conservation of linear momentum.
1. Understanding the System:
- We consider the bomb as a system that is initially stationary. This means that the total momentum of the system before the explosion is zero.
2. Explosion and Internal Forces:
- When the bomb explodes, it breaks into two fragments. The explosion is caused by internal forces acting within the bomb. Since these forces are internal, they do not affect the total momentum of the system.
3. Conservation of Linear Momentum:
- According to the law of conservation of linear momentum, if no external forces act on a system, the total momentum of the system remains constant. In this case, since the bomb is stationary before the explosion, the initial momentum is zero.
4. Analyzing the Fragments:
- Let’s denote the masses of the two fragments as m1 and m2, and their velocities after the explosion as v1 and v2 respectively.
- After the explosion, the fragments move in opposite directions. Therefore, we can express the final momentum of the system as:
m1v1+m2v2=0
- This implies that m1v1=−m2v2. The negative sign indicates that the velocities are in opposite directions.
5. Conclusion:
- Since the total momentum before the explosion (initial momentum) is zero and the total momentum after the explosion (final momentum) is also zero, the law of conservation of linear momentum is upheld.
- Therefore, both the assertion and the reason are true, and the reason correctly explains the assertion.
Final Answer:
- Both the assertion (A) and the reason (R) are true, and R is the correct explanation for A.
- We consider the bomb as a system that is initially stationary. This means that the total momentum of the system before the explosion is zero.
- When the bomb explodes, it breaks into two fragments. The explosion is caused by internal forces acting within the bomb. Since these forces are internal, they do not affect the total momentum of the system.
- According to the law of conservation of linear momentum, if no external forces act on a system, the total momentum of the system remains constant. In this case, since the bomb is stationary before the explosion, the initial momentum is zero.
- Let’s denote the masses of the two fragments as m1 and m2, and their velocities after the explosion as v1 and v2 respectively.
- After the explosion, the fragments move in opposite directions. Therefore, we can express the final momentum of the system as:
m1v1+m2v2=0
- This implies that m1v1=−m2v2. The negative sign indicates that the velocities are in opposite directions.
- Since the total momentum before the explosion (initial momentum) is zero and the total momentum after the explosion (final momentum) is also zero, the law of conservation of linear momentum is upheld.
- Therefore, both the assertion and the reason are true, and the reason correctly explains the assertion.
- Both the assertion (A) and the reason (R) are true, and R is the correct explanation for A.
Similar Questions
A stationary body explodes into two fragments of masses m1 and m2. If momentum of one fragment is p, the energy of explosion is
View SolutionA stationary body explodes into two fragments of masses m1 and m2. If momentum of one fragment is p, the energy of explosion is
View SolutionIn an experiment on photoelectric effect, a photon is incident on an electron from one direction and the photoelectron is emitted almost in the opposite direction. Does this violate conservation of momentum ?
View SolutionA grenade having mass of 10 kg flying horizontally with a velocity of 10 m/s explodes into two fragments. The larger fragment has a velocity of 25 m/s in the direction of the intial velocity of the grenade. The smaller fragment has a velocity of 12.5 m/s in the opposite dirction. The masses of the fragments are
View SolutionA bomb is projected with speed 10 m/s at an angle 30o with the horizontal. In the mid-air bomb explodes in different fragments and they all move in different directions. At the time when all fragments reach at ground, the displacement of the center of mass of bomb from initial point will be (g = 10 m/s2)
View SolutionSTATEMENT-1 : A person standing on a stationary trolley placed on rough ground walks for a moment and then stops. The system acquires a net velocity due to this.

and
STATEMENT-2 : In the present situation, law of conservation of linear momentum is violated.
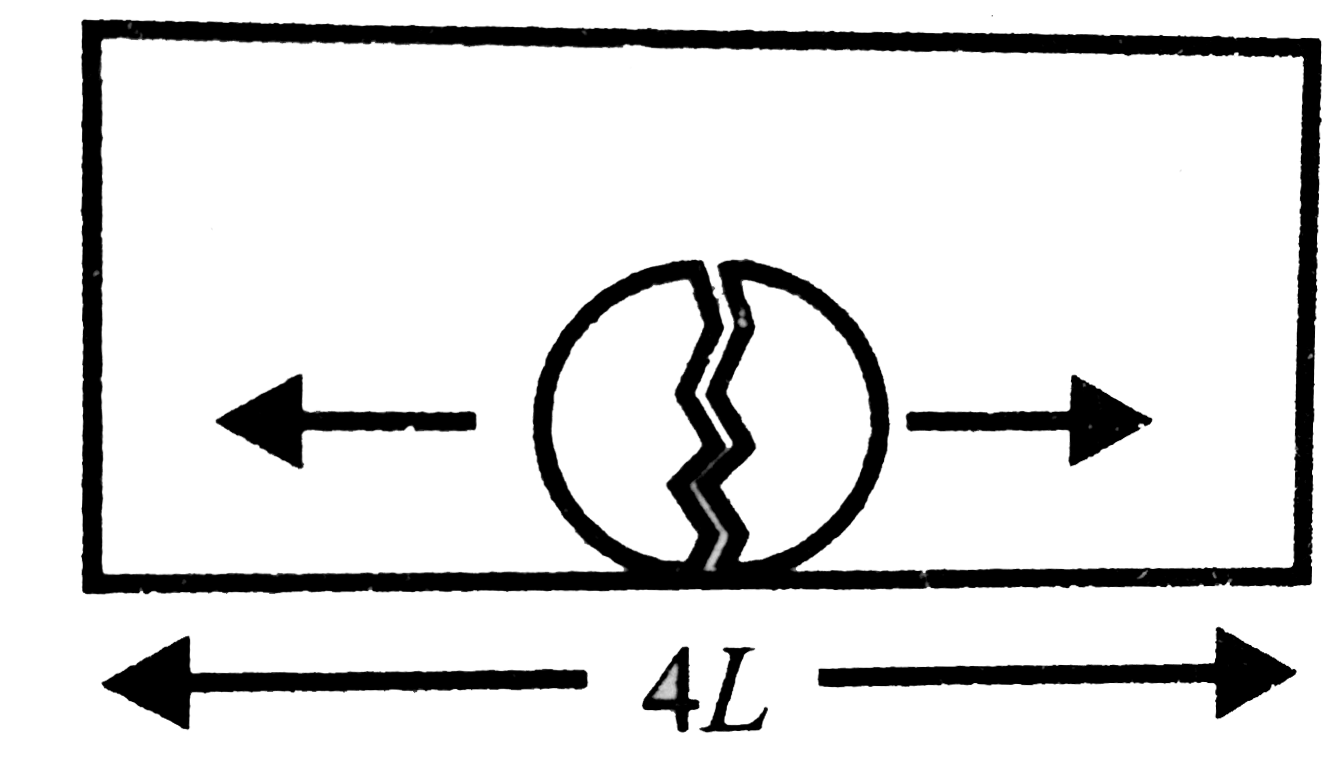
View SolutionA bomb of mass 3m is kept inside a closed box of mass 3m and length 4L at its centre. It explodes in two parts of mass m and 2m. The two parts move in opposite directions and stick to the opposite sides of the walls of box. The box is kept on a smooth horizontal surface. What is the distance moved by the box during this time interval.
View SolutionA shell of mass 2kg moving at a rate of 4m/s suddenly explodes into two equal fragments. The fragments go in directions inclined with the original line of motion with equal velocities, If the explosion imparts 48J of translational kinetic energy to the fragments, find the velocity and direction of each fragment.
View SolutionAt high altitude , a body explodes at rest into two equal fragments with one fragment receiving horizontal velocity of 10m/s. Time taken by the two radius vectors connecting of explosion to fragments to make 90∘ is
View SolutionA stationary particle explodes into two particles of masses x and y, which move in opposite directions wit h velocity v1andv2. The ratio of their kinetic energies (E1:E2) is
View Solution
