Two blocks are connected by a string, as shown in figure. They are released from rest. Show that after they have moved a distance L, their common speed is given by v=√2(m2−μm1)gL/(m1+m2), in which μ is the coefficient of kinetic friction between the upper block and the surface. Assume that the pulley is massless and frictionless.
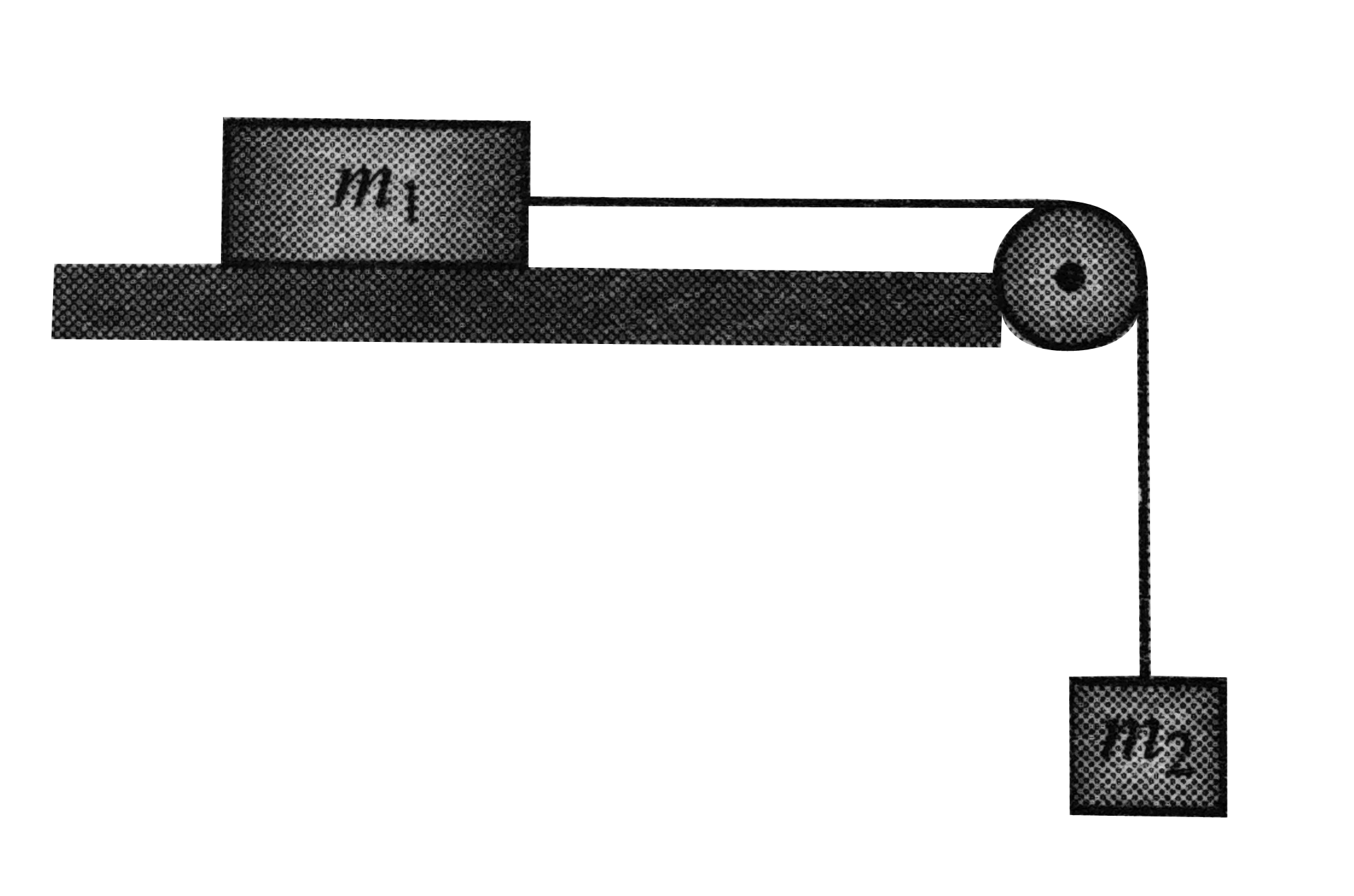
In moving a distance L by m1 and m2 the PE will be lost by m2 only and will be m2gL, while work done by friction will be only on m1 and will be μm1gL. Now as the string is inextensible v1=v2=v and so, the gain in KE will be =(1/2)(m1+m2)v2. By conservation of energy.
Loss in PE = Gain in KE + WD against friction
i.e., m2gL=12(m1+m2)v2+μm1gL
v=√2(m2−μm1)gL(m1+m2)
Similar Questions
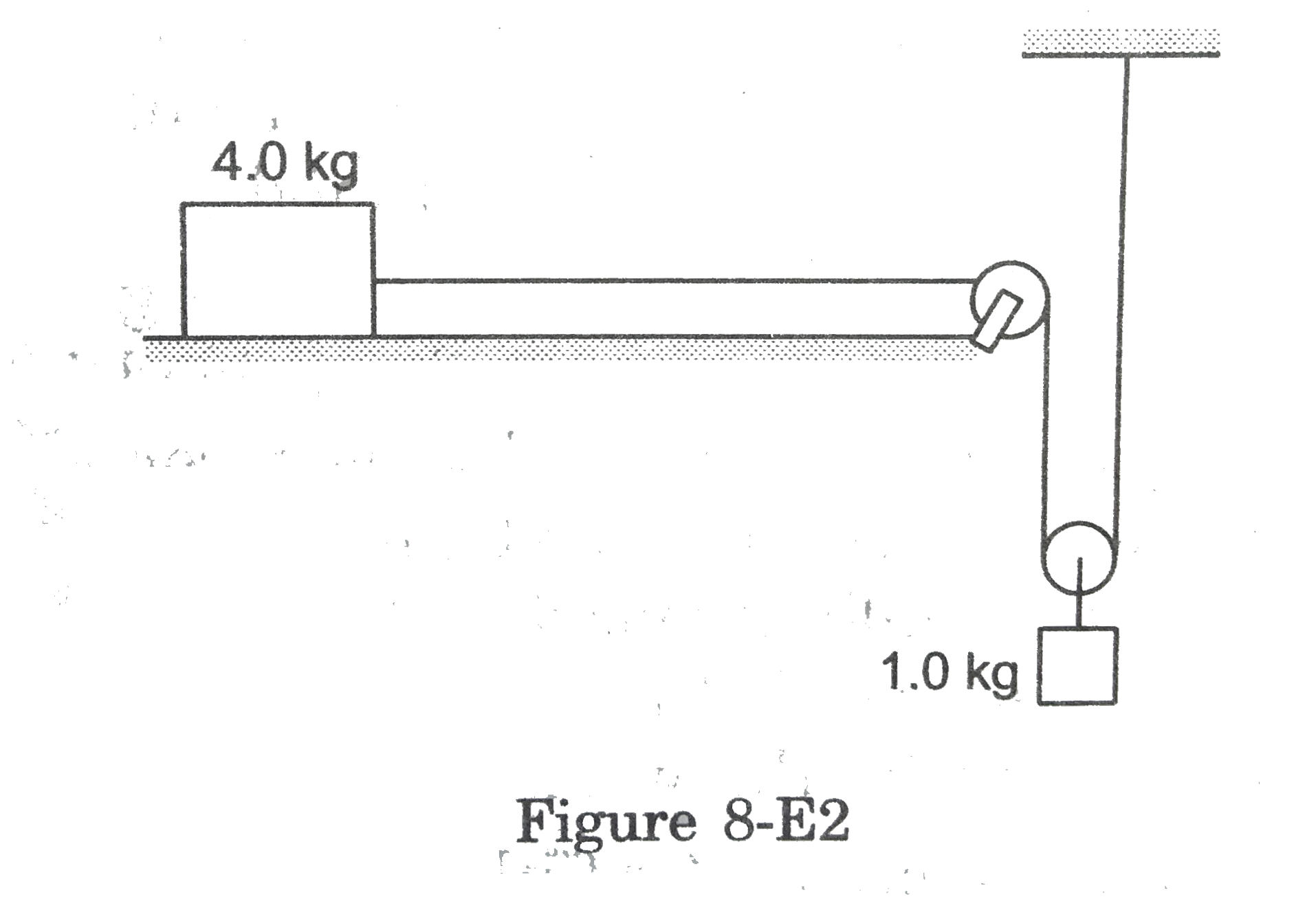
Consider the situatioin shown in figure. The system is released from rest and the block of mass 1.0 kg is found to have a speed 0.3 m/s ater it has descended thrugh a distance of 1 m. find the coefficient of kinetic friction between the block and the table.
View SolutionA block of mass m is moving on a rough horizontal surface. μ is the coefficient of kinetic friction between the block and the surface. What is the net force exerted by the surface on the block?
View Solution
Two blocks of masses m1 and m2 are connected as shown in the figure. The acceleration of the block m2 is :
View SolutionIn the figure given below, with what acceleration does the block of mass m will move? (Pulley and strings are massless and frictionless)
View SolutionTwo block of masses m1 and m2 are connected as shown in the figure. The acceleration of the block m2 is:

View SolutionTwo blocks are connected by a long inextensible string passing over an ideal pulley as shown in the figure. If the system is released from rest then the common speed of blocks when block m2 moves a distance I will be
View SolutionIn the figure given below , with what acceleration does the block of mass m will move ? ( Pulley and strings are massless and frictionless)

View SolutionFind the relation between acceleration of the two blocks m1andm2. Assume pulleys are massless and frictionless and the strings are inextensible .
View SolutionTwo blocks of equal masses are connected by an ideal string passing over an ideal pulley as shown in the figure
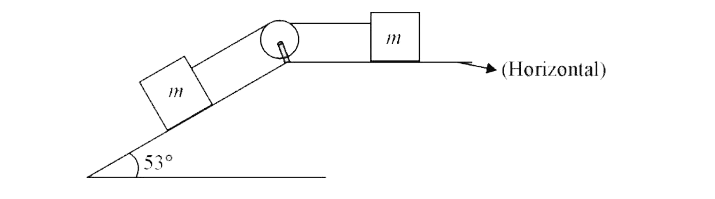
All the surfaces in contact with blocks are rough having coefficient of kinetic friction μ between them. If the blocks slide with constant velocity, find the value of μ
View SolutionTwo block of masses M and m are connected to each other by a massless string and spring of force constant k as shown in the figure. The spring passes over a frictionless pulley connected rigidly to the egde of a stationary block A. The coefficient of friction between block M and plane horizontal surface of A is μ. The block M slides over the horizontal top surface of A and block m slides vertically downward with the same speed. The mass M is equal to

View Solution