Find the work done in lifting a stone of mass 10 kg and specife gravity 3 from the bed of a lake a height of 6 m in water.
Mass of stone = 10 kg , Specific gravity =dsdw=3
W=mgh(1−dwds)=10×9.8×6×(1−13)
W=98×6×23=392J
Similar Questions
What is the work done in taking an object of mass 1kg from the surface of the earth to a height equal to the radius of the earth ?
(G=6.67×10−11Nm2/Kg2, Radius of the earth = 6400 km, Mass of the earth =6×1024kg.)View SolutionThe work that must be done in lifting a body of weight P from the surface of the earth to a height h is
View Solution
Knowledge Check
- Question 1 - Select One
If a body of mass 5 kg is lifted from the ground level to a height of 5m then ratio of its inertia is …………..
A1:1BsameCconstantDnot defined
Find work done in shifting a body of mass m from a height h above the earth's surface to a height 2h above the earth's surface..
View SolutionIf the acceleration due to gravity at the surface of the earth is g, the work done in slowly lifting a body ofmass m from the earth's surface to a height R equal to the radius of the earth is
View SolutionThe work done by gravitational force on a point mass m0in moving from the surface of a planet off mass M and radius R to a height R2 is
View SolutionA uniform rod of length 2.0 m specific gravity 0.5 and mass 2 kg is hinged at one end to the bottom of a tank of water (specific gravity = 10) filled upto a height o f 1.0 m as shown in figure. Taking the case θ=−0∘ the force exerted by the hings on the rod is (g=10m/s2)
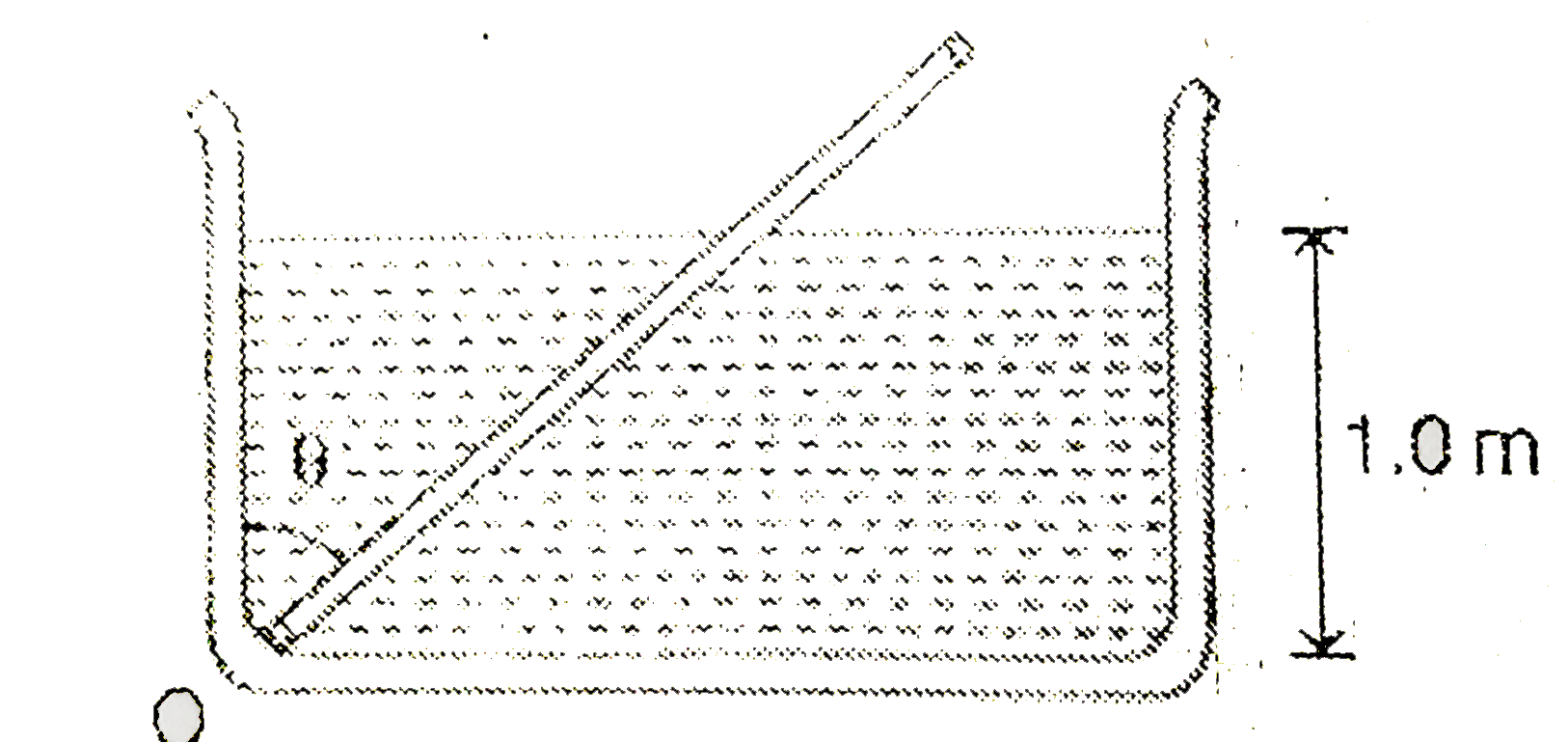 View Solution
View SolutionThe liquids shown in figure in the two arms are mercury (specific gravity =13.6) and water. If the difference of heights of the mercury columns is 2 cm, find the height of the water column.
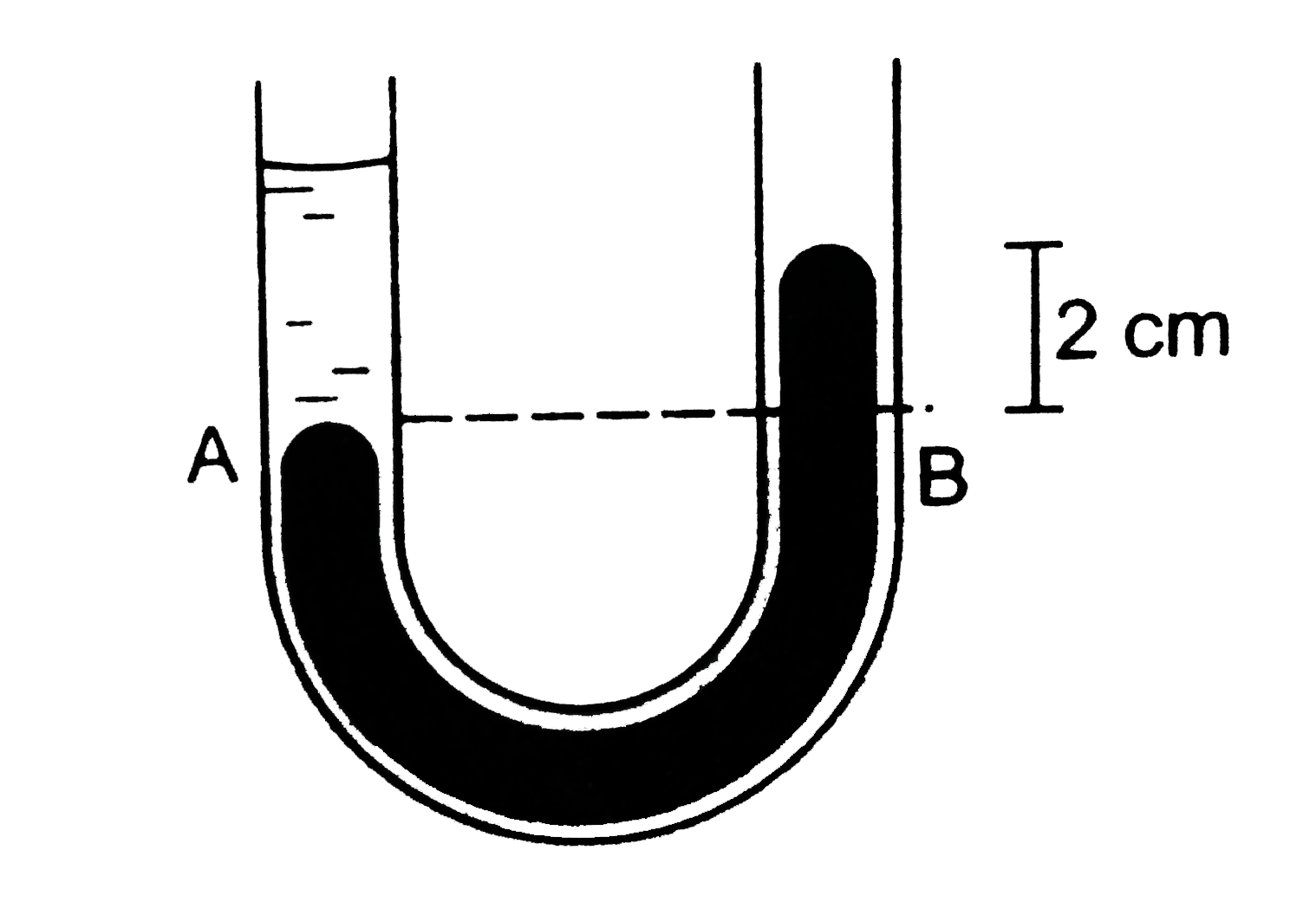 ,View Solution
,View SolutionThe liquids shown in figure in the two arms are mercury (specific gravity =13.6) and water. If the difference of heights of the mercury columns is 2 cm, find the height of the water column.
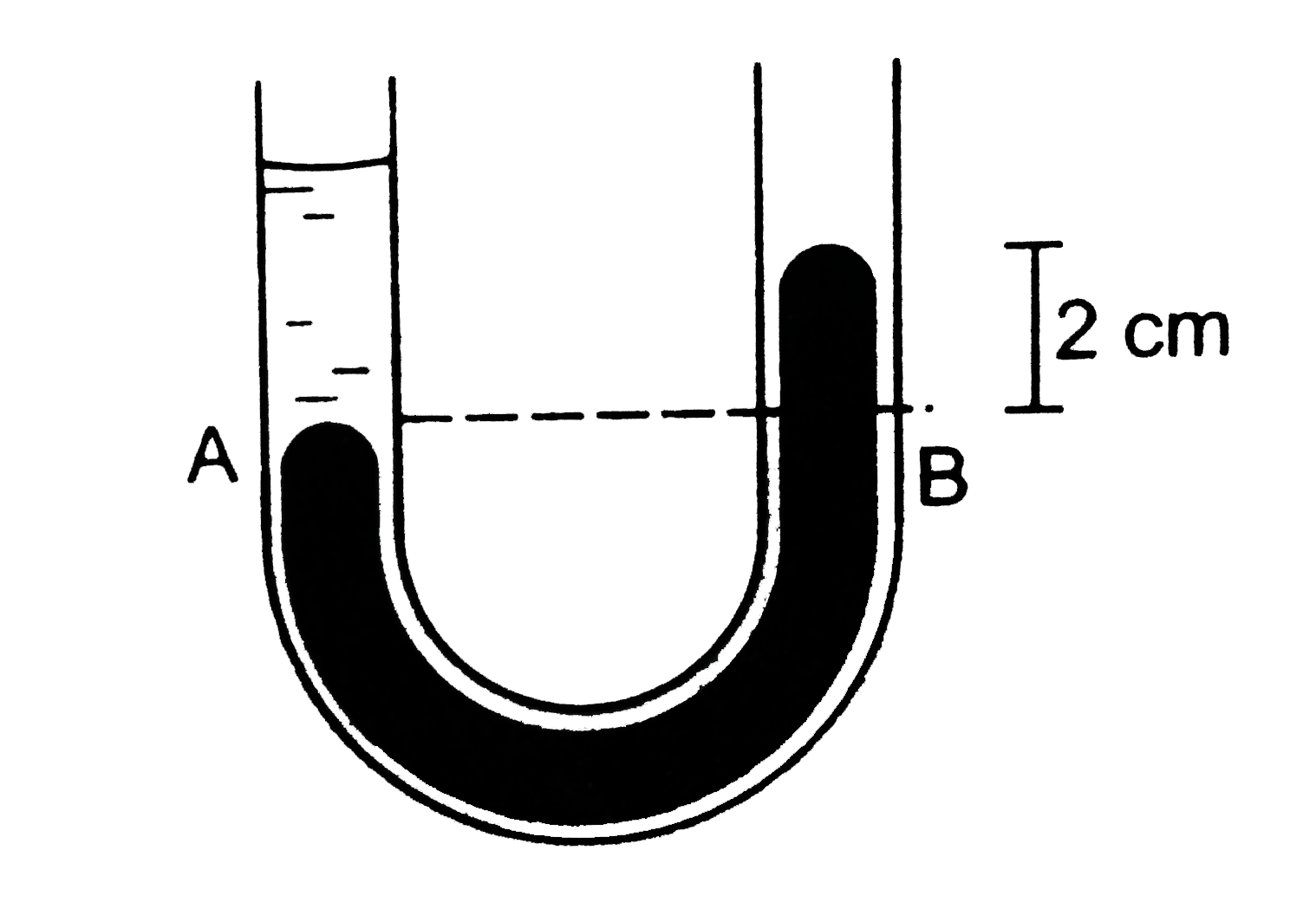 ,View Solution
,View SolutionThe work done in pushing a block of mass 10 kg from bottom to the top of a frictionless inclined plane 5 m long and 3 m high is-
(g=9.8m/sec2)View Solution
