A cube of edge a has its edges parallel to X, Y and Z -axis of rectangular coordinate system. A uniform electric held E is parallel to Y-axis and uniform magnetic field B parallel to x axis. The rate at which energy flows through each face of the cube is
a2EB2μ0 parallel to X-Y plane and zero in others
a2EBμ0 parallel to Y-Z plane and zero in others
a2EB2μ0from all faces
a2EB2μ0 parallel to X-Z faces and zero in others
The correct Answer is:B
To solve the problem of determining the rate at which energy flows through each face of a cube in the presence of a uniform electric field E and a uniform magnetic field B, we can follow these steps:
1. Understanding the Configuration:
- We have a cube with edge length a.
- The electric field E is directed along the Y-axis (let's denote it as ^j).
- The magnetic field B is directed along the X-axis (denote it as ^i).
2. Using the Poynting Vector:
- The Poynting vector →S represents the rate of energy flow per unit area and is given by the formula:
→S=1μ0→E×→B
- Here, μ0 is the permeability of free space.
3. Calculating the Cross Product:
- We need to calculate →E×→B:
→E=E^j,→B=B^i
→E×→B=(E^j)×(B^i)=EB(^j×^i)
- The cross product ^j×^i=−^k (using the right-hand rule).
4. Substituting into the Poynting Vector:
- Therefore, we have:
→S=1μ0EB(−^k)=−EBμ0^k
- This indicates that the energy flows in the negative Z-direction.
5. Calculating the Rate of Energy Flow:
- The magnitude of the Poynting vector is:
|→S|=EBμ0
- The area of each face of the cube is A=a2.
6. Finding the Total Energy Flow Through Each Face:
- The rate of energy flow through the face of the cube perpendicular to the Z-axis (which is the XY-plane) is:
Rate of energy flow=|→S|⋅A=EBμ0⋅a2
7. Final Result:
- Thus, the rate at which energy flows through the face of the cube that is parallel to the XY-plane is:
Rate of energy flow=EBa2μ0
- For the other faces (YZ-plane and XZ-plane), since the Poynting vector is directed along the Z-axis, the energy flow through those faces is zero.
Summary:
- The rate at which energy flows through the faces of the cube is:
- EBa2μ0 through the XY-plane,
- 0 through the YZ-plane and XZ-plane.
- We have a cube with edge length a.
- The electric field E is directed along the Y-axis (let's denote it as ^j).
- The magnetic field B is directed along the X-axis (denote it as ^i).
- The Poynting vector →S represents the rate of energy flow per unit area and is given by the formula:
→S=1μ0→E×→B
- Here, μ0 is the permeability of free space.
- We need to calculate →E×→B:
→E=E^j,→B=B^i
→E×→B=(E^j)×(B^i)=EB(^j×^i)
- The cross product ^j×^i=−^k (using the right-hand rule).
- Therefore, we have:
→S=1μ0EB(−^k)=−EBμ0^k
- This indicates that the energy flows in the negative Z-direction.
- The magnitude of the Poynting vector is:
|→S|=EBμ0
- The area of each face of the cube is A=a2.
- The rate of energy flow through the face of the cube perpendicular to the Z-axis (which is the XY-plane) is:
Rate of energy flow=|→S|⋅A=EBμ0⋅a2
- Thus, the rate at which energy flows through the face of the cube that is parallel to the XY-plane is:
Rate of energy flow=EBa2μ0
- For the other faces (YZ-plane and XZ-plane), since the Poynting vector is directed along the Z-axis, the energy flow through those faces is zero.
- The rate at which energy flows through the faces of the cube is:
- EBa2μ0 through the XY-plane,
- 0 through the YZ-plane and XZ-plane.
Topper's Solved these Questions
- BOOK - AAKASH SERIESCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - EXERCISE -IB37videos
ELECTROMAGNETIC WAVES
- BOOK - AAKASH SERIESCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - EXERCISE -II22videos
ELECTROMAGNETIC WAVES
- BOOK - AAKASH SERIESCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - EXERCISE -II22videos
ELECTROMAGNETIC WAVES
- BOOK - AAKASH SERIESCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Additional Exercise11videos
ELECTROMAGNETIC INDUCTION
- BOOK - AAKASH SERIESCHAPTER - ELECTROMAGNETICSEXERCISE - ADDITIONAL EXERCISE13videos
ELECTROMAGNETICS
Similar Questions
A cylinder of radius R and length L is placed in a uniform electric field E parallel to the axis. The total flux for the surface of the cylinder is given by
View SolutionA cylinder of radius R and length L is placed in a uniform electric field E parallel to the axis. The total flux for the surface of the cylinder is given by
View Solution
Knowledge Check
- Question 1 - Select One
A rod of length l rotates with a uniform angular velocity omega about its perpendicular bisector. A uniform magnetic field B exists parallel to the axis of rotation. The potential difference between the two ends of the lrod is
ABl2ω2BzeroC(Bl2ω8)D2Bl2ω - Question 2 - Select One
An infinitely long cylinder is kept parallel to an uniform magnetic field B directed along positive z-axis. The direction of induced current as seen from the z-axis will be
Aclockwise of the positive z-axisBanticlockwise of the positive z-axisCzeroDalong the magnetic field
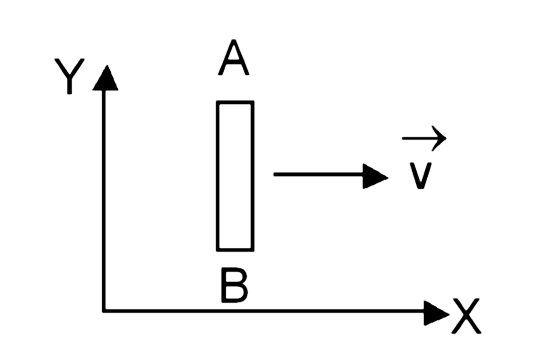
A conductor rod AB moves parallel to X-axis in a uniform magnetic field, pointing in the positive Z-direction. The end A of the rod gets-
 View Solution
View SolutionA cylinder of radius R and length l is placed in a uniform electric field E parallel to the axis of the cylinder. The total flux over the curved surface of the cylinder is
View SolutionEquipotential surfaces associated with a uniform electric field along positive x-axis are planes parallel to
View SolutionA square loop of side 10 cm with its side parallel to X, and y axis is kept in a uniform magnetic field pointing towards positive z-direction. If magnetic field changes at the rate of 0.1 T/s, then induced emf is
View SolutionA rod of length l rotates with a uniform angular velocity omega about its perpendicular bisector. A uniform magnetic field B exists parallel to the axis of rotation. The potential difference between the two ends of the lrod is
View SolutionAn infinitely long cylinder is kept parallel to an uniform magnetic field B directed along positive z-axis. The direction of induced current as seen from the z-axis will be
View Solution
