A block of mass 1 slides down a curved track that is one quadrant of a circle of radius 1m. Its speed at the bottom is 2m/s. The work done by frictional force is:
8j
−8J
4J
−4J
The correct Answer is:B
To solve the problem, we will use the principle of conservation of energy. The work done by friction can be calculated by comparing the initial potential energy of the block at the top of the track with its final kinetic energy at the bottom.
1. Identify the initial potential energy (PE):
The block is at a height (h) equal to the radius of the circular track, which is 1 meter. The potential energy at the top can be calculated using the formula:
PE=mgh
where:
- m=1kg (mass of the block)
- g=10m/s2 (acceleration due to gravity)
- h=1m (height)
Substituting the values:
PE=1×10×1=10J
2. Calculate the final kinetic energy (KE):
The kinetic energy at the bottom of the track can be calculated using the formula:
KE=12mv2
where:
- v=2m/s (speed at the bottom)
Substituting the values:
KE=12×1×(2)2=12×1×4=2J
3. Apply the work-energy principle:
The work done by friction (W_friction) can be found by comparing the initial potential energy and the final kinetic energy:
Wfriction=KE−PE
Substituting the values we found:
Wfriction=2J−10J=−8J
4. Conclusion:
The work done by frictional forces is:
Wfriction=−8J
Final Answer:
The work done by frictional force is −8J.
---
The block is at a height (h) equal to the radius of the circular track, which is 1 meter. The potential energy at the top can be calculated using the formula:
PE=mgh
where:
- m=1kg (mass of the block)
- g=10m/s2 (acceleration due to gravity)
- h=1m (height)
PE=1×10×1=10J
The kinetic energy at the bottom of the track can be calculated using the formula:
KE=12mv2
where:
- v=2m/s (speed at the bottom)
KE=12×1×(2)2=12×1×4=2J
The work done by friction (W_friction) can be found by comparing the initial potential energy and the final kinetic energy:
Wfriction=KE−PE
Substituting the values we found:
Wfriction=2J−10J=−8J
The work done by frictional forces is:
Wfriction=−8J
The work done by frictional force is −8J.
Similar Questions
A block of mass 1 kg slides down a vertical curved track that is one quadrant of a circle of radius 1m. Its speed ast the the bottom si 2m/s. The work done by frictional force is :

View SolutionA block of mass 1kg slides down a curved track which forms one quadrant of a circle of radius 1m as shown in figure. The speed of block at the bottom of track is v=2ms−1. The work done by the of friction is
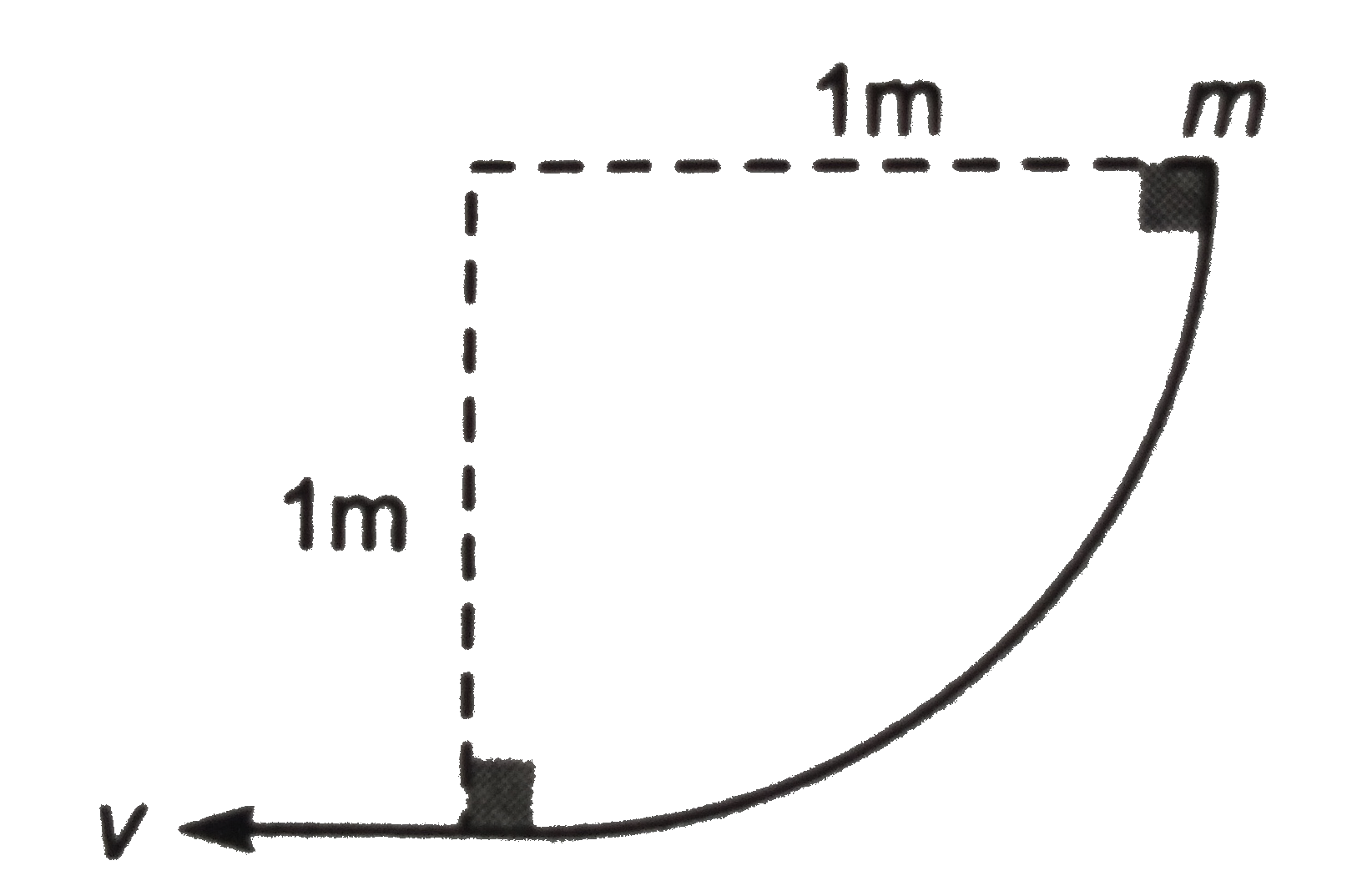 .
.
View Solution
A block of mass 1 kg is pulled slowly along the curve path ACB by a tangential force as shown in figure. The magnitude of work done by the frictional force when the block moves from A to B is
View SolutionA block of mass 50 kg slides over a horizontal distance of 1m. If the coefficient of friction between their surface is 0.2, then work done against friction is (take g=9.8m/s2) :
View SolutionA block of mass m slides down a smooth vertical circular track. During the motion, the block is in
View SolutionWhen a body of mass M slides down an inclined plane of inclination θ, having coefficient of friction μ through a distance s, the work done against friction is :
View SolutionA body of mass 1 kg is rotated in a horizontal circle of radius 1 m and moves with velocity 2ms−1 The work done in 10 revolutions is
View SolutionA block of mass m at the end of a string is whirled round in a vertical circle of radius R. The critical speed of the block at top of its swing below which the string would slacken before the block reaches the bottom is?
View SolutionA block of mass m slides down along the surface of the bowl from the rim to the bottom as shown in fig. The velocity of the block at the bottom will be-

View SolutionA block of mass m is stationary with respect to the wedge of mass M moving with uniform speed v on horizontal surface. Work done by friction force on the block in t seconds is
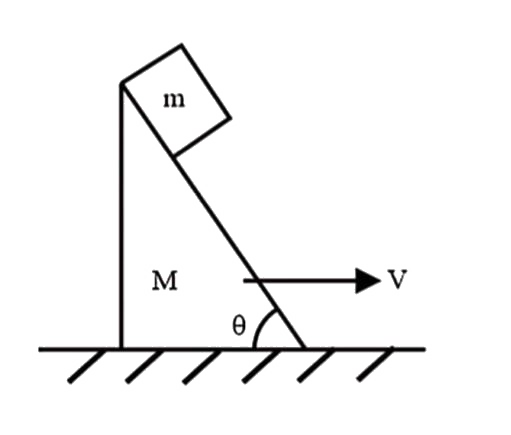
View Solution