The work done in lifting a body of mass 20 kg and specific gravity 3.2 to a height of 8m in water is (g=10ms−2)
110J
1600 J
500 j
1100 J
The correct Answer is:D
To solve the problem of calculating the work done in lifting a body of mass 20 kg and specific gravity 3.2 to a height of 8 m in water, we will follow these steps:
Step 1: Understand Specific Gravity
Specific gravity (SG) is defined as the ratio of the density of a substance to the density of water. Given that the specific gravity of the body is 3.2, we can express the density of the body (ρ_b) in terms of the density of water (ρ_w).
ρb=SG×ρw
Where:
- ρ_w (density of water) = 1000 kg/m³
- SG = 3.2
Step 2: Calculate the Density of the Body
Using the formula from Step 1, we can calculate the density of the body:
ρb=3.2×1000kg/m3=3200kg/m3
Step 3: Determine the Weight of the Body
The weight (W) of the body can be calculated using the formula:
W=m⋅g
Where:
- m = mass of the body = 20 kg
- g = acceleration due to gravity = 10 m/s²
Calculating the weight:
W=20kg×10m/s2=200N
Step 4: Calculate the Work Done in Lifting the Body
The work done (W_d) in lifting the body in a fluid can be calculated using the formula:
Wd=mgh(1−ρwρb)
Where:
- h = height = 8 m
- ρ_w = density of water = 1000 kg/m³
- ρ_b = density of the body = 3200 kg/m³
Substituting the values into the formula:
Wd=20kg×10m/s2×8m(1−10003200)
Step 5: Simplify the Calculation
First, calculate the fraction:
10003200=0.3125
Now substituting this back into the work done formula:
Wd=20×10×8(1−0.3125)
Calculating 1−0.3125:
1−0.3125=0.6875
Now substituting this value:
Wd=20×10×8×0.6875
Calculating the product:
Wd=1600×0.6875=1100J
Final Answer
The work done in lifting the body is 1100 Joules.
---
Specific gravity (SG) is defined as the ratio of the density of a substance to the density of water. Given that the specific gravity of the body is 3.2, we can express the density of the body (ρ_b) in terms of the density of water (ρ_w).
- ρ_w (density of water) = 1000 kg/m³
- SG = 3.2
Using the formula from Step 1, we can calculate the density of the body:
The weight (W) of the body can be calculated using the formula:
- m = mass of the body = 20 kg
- g = acceleration due to gravity = 10 m/s²
The work done (W_d) in lifting the body in a fluid can be calculated using the formula:
- h = height = 8 m
- ρ_w = density of water = 1000 kg/m³
- ρ_b = density of the body = 3200 kg/m³
First, calculate the fraction:
The work done in lifting the body is 1100 Joules.
Similar Questions
Knowledge Check
A crane lifts a mass of 100 kg to a height of 10 m in 20 s. The power of the crane is (Take g=10ms−2)
A100 WB200 WC250 WD500 W
If 250 J of work is done in sliding a 5 kg block up an inclined plane of height 4 m. Work done against friction is (g=10ms−2)
View SolutionIf the acceleration due to gravity at the surface of the earth is g, the work done in slowly lifting a body ofmass m from the earth's surface to a height R equal to the radius of the earth is
View SolutionWater is drawn from a well in a 5kg drum of capacity 55L by two ropes connected to the top of the drum. The linear mass density of each rope is 0.5kgm−1. The work done in lifting water to the ground from the surface of water in the well 20m below is
[g=10ms−2]
View SolutionThe work done in slowly lifting a body from earth's surface to a height R (radius of earth) is equal to two times the work done in lifting the same body from earth's surface to a height h. Here h is equal to
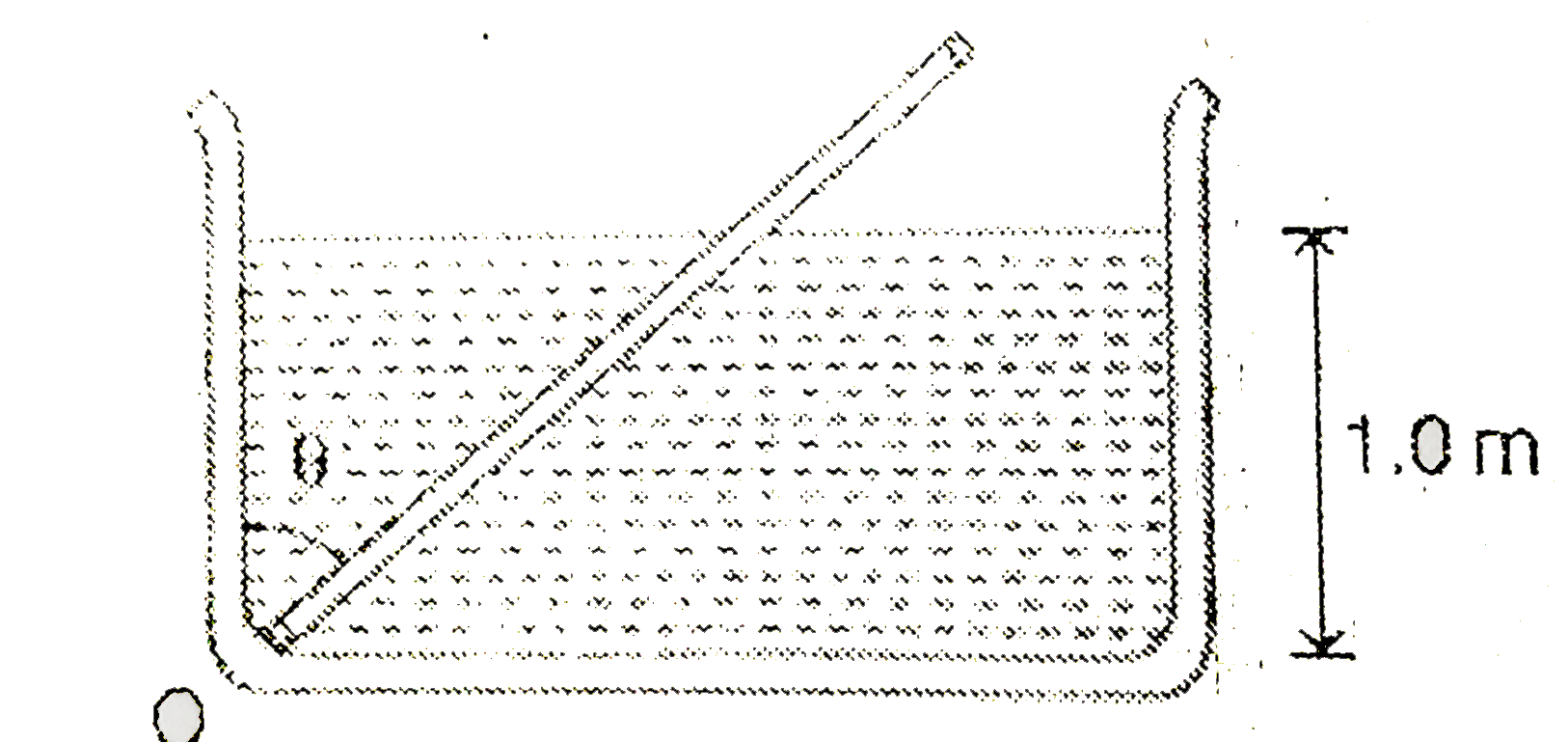
View SolutionA uniform rod of length 2.0 m specific gravity 0.5 and mass 2 kg is hinged at one end to the bottom of a tank of water (specific gravity = 10) filled upto a height o f 1.0 m as shown in figure. Taking the case θ=−0∘ the force exerted by the hings on the rod is (g=10m/s2)
View SolutionA beaker containing water is kept on a spring scale. The mass of water and beaker is 5 kg . A block of mass 2 kg and specific gravity 10 is suspended by means of thread from a spring balance as shown. The readings of scales S1 and S2 are respectively Take, g=10ms−2

View SolutionA body of mass 5 kg is taken a height 5 m to 10 m .Find the increase in its potential energy (g=10 m s−2)
View Solution
