The ratio of energy required to accelerated a car from rest to 20ms−1 to the energy needed to acceelerate from 20ms−1 to 40ms−1 is
1:1
1:3
1:2
1:4
The correct Answer is:B
To solve the problem of finding the ratio of energy required to accelerate a car from rest to 20m/s and from 20m/s to 40m/s, we will use the concept of kinetic energy. The work done in accelerating the car is equal to the change in kinetic energy.
1. Understanding Kinetic Energy:
The kinetic energy (KE) of an object is given by the formula:
KE=12mv2
where m is the mass of the object and v is its velocity.
2. Calculate the Energy Required to Accelerate from Rest to 20m/s:
- Initial velocity u1=0m/s (at rest)
- Final velocity v1=20m/s
- Change in kinetic energy (ΔKE1):
ΔKE1=KEfinal−KEinitial=12m(v21)−12m(u21)
ΔKE1=12m(202)−12m(02)=12m(400)=200m
3. Calculate the Energy Required to Accelerate from 20m/s to 40m/s:
- Initial velocity u2=20m/s
- Final velocity v2=40m/s
- Change in kinetic energy (ΔKE2):
ΔKE2=KEfinal−KEinitial=12m(v22)−12m(u22)
ΔKE2=12m(402)−12m(202)=12m(1600)−12m(400)
ΔKE2=12m(1600−400)=12m(1200)=600m
4. Finding the Ratio of Energies:
Now we can find the ratio of the energy required for the two cases:
Ratio=ΔKE1ΔKE2=200m600m=200600=13
5. Final Answer:
The ratio of the energy required to accelerate from rest to 20m/s to the energy needed to accelerate from 20m/s to 40m/s is:
1:3
The kinetic energy (KE) of an object is given by the formula:
KE=12mv2
where m is the mass of the object and v is its velocity.
- Initial velocity u1=0m/s (at rest)
- Final velocity v1=20m/s
- Change in kinetic energy (ΔKE1):
ΔKE1=KEfinal−KEinitial=12m(v21)−12m(u21)
ΔKE1=12m(202)−12m(02)=12m(400)=200m
- Initial velocity u2=20m/s
- Final velocity v2=40m/s
- Change in kinetic energy (ΔKE2):
ΔKE2=KEfinal−KEinitial=12m(v22)−12m(u22)
ΔKE2=12m(402)−12m(202)=12m(1600)−12m(400)
ΔKE2=12m(1600−400)=12m(1200)=600m
Now we can find the ratio of the energy required for the two cases:
Ratio=ΔKE1ΔKE2=200m600m=200600=13
The ratio of the energy required to accelerate from rest to 20m/s to the energy needed to accelerate from 20m/s to 40m/s is:
1:3
Similar Questions
The energy required to accelerate a car from 10 m/s to 20 m / s is how many times the energy required to accelerate the car from rest to 10 m /s
View Solution(a) Find the energy needed to remove a neutron from the nucleus of the calcium isotope .4220Ca.
(b) Find the energy needed to remove a proton from this nucleus.
(c ) Why are these energies different? Mass of .4020Ca=40.962278u, mass of proton =1.007825u.
View Solution
Knowledge Check
A person in an elevator accelerating upwards with an acceleration of 2ms−2 , tosses a coin vertically upwards with a speed of 20ms−1 . After how much time will the coin fall back into his hand ? (g = 10 ms−2)
A53sB310sC103sD35s
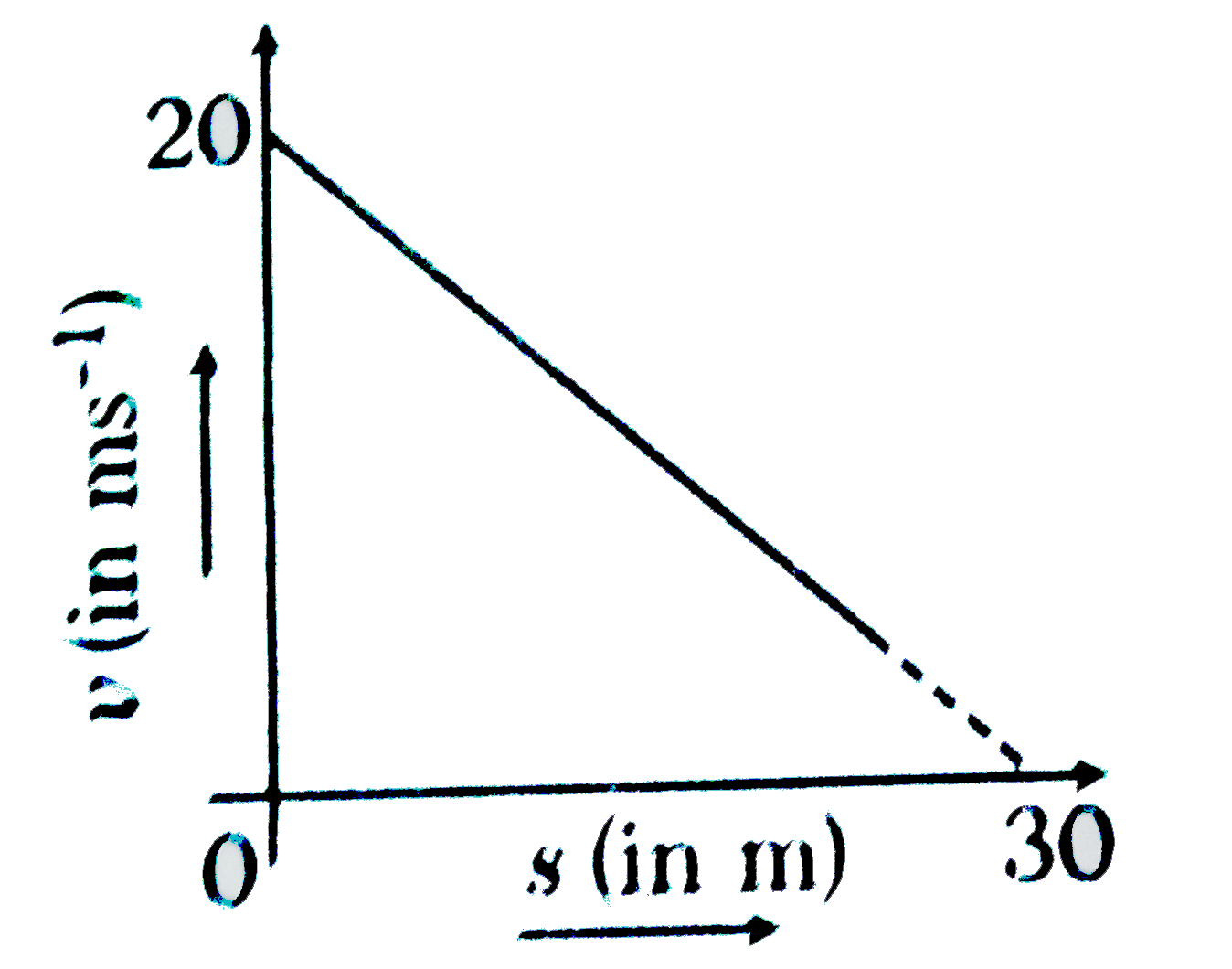
If the velocity v of particle moving along a straight line decreases linearly with its displacement s from 20ms−1 to a value approaching zero at s = 30 m, then acceleration of the particle at v=10ms^(-1) is
View SolutionA person in an elevator accelerating upwards with an acceleration of 2ms−2 , tosses a coin vertically upwards with a speed of 20ms−1 . After how much time will the coin fall back into his hand ? (g = 10 ms−2)
View SolutionA person in an elevator accelerating upwards with an acceleration of 2ms−2 , tosses a coin vertically upwards with a speed of 20ms−1 . After how much time will the coin fall back into his hand ? (g = 10 ms−2)
View SolutionA particle travels in a circle of radius 20 cm at a uniformly increasing speed. If the speed changes from 8ms−1 to 9ms−1 in 2s, what would be the angular acceleration in rad s−2 ?
View SolutionThe potential energy of a projectile at its maximum height is equal to its kinetic energy there. If the velocity of projection is 20 ms−1 , its time of flight is (g=10 ms−2 )
View SolutionA body starts at t=0 with velcoity u and travels along a straight linge. The body has a constant acceleration(a). Draw the acceleration-time graph from t=0 to t=10s for the following cases:
a. u=8ms−1, a=2s^(-2)<br>b.u=8 ms^(-1),a=−2ms−2
c. u=−8ms−1 ,a=2 ms^(-2)<br>d.u=-8ms^(-1),a=−2ms−2.
View SolutionThe electric motor of a model train accelrates the train from rest to 0.620ms−1 in 21.0ms. The total mass of the train is 875g. Find the average power delivered to the train during the acceleration.
View Solution

