In a woody dicot stem twenty spring woods and twenty autumn woods are present. What is the approximate age of that tree
10 Years
40 Years
5 Years
20 Years
The correct Answer is:D
To determine the approximate age of a woody dicot stem with 20 spring woods and 20 autumn woods, we can follow these steps:
1. Understand the Structure of the Tree Rings:
- In woody dicotyledonous plants, the growth rings (or annual rings) are formed each year. Each year typically consists of two types of wood: spring wood (formed during the growing season) and autumn wood (formed later in the year).
2. Identify the Number of Rings:
- The problem states that there are 20 spring woods and 20 autumn woods present in the stem.
3. Calculate Total Annual Rings:
- Each year contributes one spring wood and one autumn wood. Therefore, the total number of annual rings is the sum of the spring and autumn woods.
- Total annual rings = Number of spring woods + Number of autumn woods = 20 + 20 = 40.
4. Determine the Age of the Tree:
- Since each pair of spring and autumn woods represents one year of growth, we can calculate the age of the tree by dividing the total number of rings by 2 (since each year contributes one spring and one autumn wood).
- Age of the tree = Total annual rings / 2 = 40 / 2 = 20 years.
5. Conclusion:
- The approximate age of the tree is 20 years.
Final Answer:
The approximate age of the tree is 20 years.
---
- In woody dicotyledonous plants, the growth rings (or annual rings) are formed each year. Each year typically consists of two types of wood: spring wood (formed during the growing season) and autumn wood (formed later in the year).
- The problem states that there are 20 spring woods and 20 autumn woods present in the stem.
- Each year contributes one spring wood and one autumn wood. Therefore, the total number of annual rings is the sum of the spring and autumn woods.
- Total annual rings = Number of spring woods + Number of autumn woods = 20 + 20 = 40.
- Since each pair of spring and autumn woods represents one year of growth, we can calculate the age of the tree by dividing the total number of rings by 2 (since each year contributes one spring and one autumn wood).
- Age of the tree = Total annual rings / 2 = 40 / 2 = 20 years.
- The approximate age of the tree is 20 years.
The approximate age of the tree is 20 years.
Topper's Solved these Questions
- HISTOLOGY AND ANATOMY OF FLOWERING PLANTSBOOK - AAKASH SERIESCHAPTER - HISTOLOGY AND ANATOMY OF FLOWERING PLANTSEXERCISE - EXERCISE - II
214 Videos
- HISTOLOGY AND ANATOMY OF FLOWERING PLANTSBOOK - AAKASH SERIESCHAPTER - HISTOLOGY AND ANATOMY OF FLOWERING PLANTSEXERCISE - EXERCISE - III (PREVIOUS AIPMT/NEET QUESTIONS)
24 Videos
- HISTOLOGY AND ANATOMY OF FLOWERING PLANTSBOOK - AAKASH SERIESCHAPTER - HISTOLOGY AND ANATOMY OF FLOWERING PLANTSEXERCISE - EXERCISE - I (ANATOMY OF DICOTYLEDONOUS AND MONOCOTYLEDONOUS PLANTS)
60 Videos
- ENVIRONMENTAL ISSUESBOOK - AAKASH SERIESCHAPTER - ENVIRONMENTAL ISSUESEXERCISE - Exercise-III (Previous AIPMT/NEET Questions)
41 Videos
- HUMAN HEALTH DISEASEBOOK - AAKASH SERIESCHAPTER - HUMAN HEALTH DISEASEEXERCISE - EXERCISE - III (PREVIOUS AIPMT/NEET QUESTIONS)
56 Videos
Similar Questions
Spring wood and Autumn wood are found in
View SolutionSpring wood and Autumn wood are found in
View SolutionObserve this image of a cut section of the tree . What would be the approximate age of this tree ?

View SolutionWhat is autumn wood called as?
View SolutionDifferentiate between the following
Spring wood and Autumn wood
View SolutionA cut trunk shows 26 concentric rings of spring wood and autum wood in alternate rows. The age of trunk would be
View Solution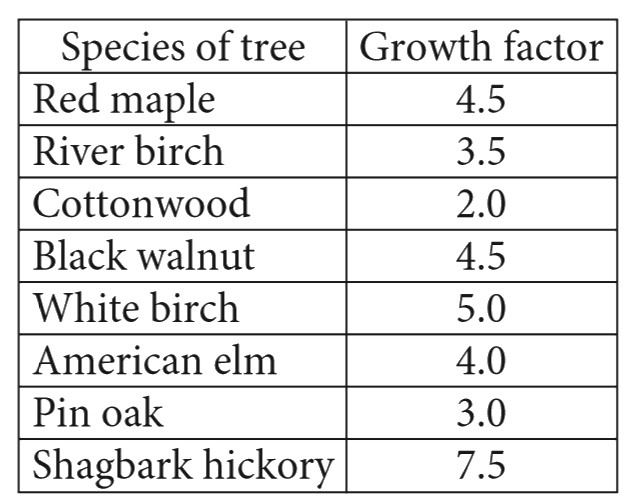
One method of calculating the approximate age , in years, of a tree of a particular species is to multiply the diameter of the tree, in inches, by a constant called the growth factor for that species. The table above gives the growth factors for eight species of trees.
According to the information in the table,what is the approximate age of an America nelm tree with a diameter of 12inches
View SolutionWhat is the dead wood present in the centre of a tree known as?
View SolutionSpring wood (early wood) differs with autumn wood (late wood) in-
View SolutionWhat is the difference in the appearance of spring and autumn wood?
View Solution
