A block of mass 10 kg is placed on a rough horizontal surface of coefficient of friction 0.1. A pulling force of 100 N acts on it at 37∘ with the horizontal. The frictional force acting on the body is ..... N.
2
4
6
7
The correct Answer is:B
To solve the problem step by step, we will analyze the forces acting on the block and calculate the frictional force.
Step 1: Identify the given data
- Mass of the block (m) = 10 kg
- Coefficient of friction (μ) = 0.1
- Pulling force (F) = 100 N
- Angle of pulling force (θ) = 37°
Step 2: Calculate the weight of the block
The weight (W) of the block can be calculated using the formula:
W=m⋅g
Where g (acceleration due to gravity) is approximately 10m/s2.
W=10kg⋅10m/s2=100N
Step 3: Resolve the pulling force into components
The pulling force can be resolved into horizontal (F_x) and vertical (F_y) components:
- Horizontal component:
Fx=F⋅cos(θ)=100⋅cos(37°)
Using cos(37°)≈45=0.8:
Fx=100⋅0.8=80N
- Vertical component:
Fy=F⋅sin(θ)=100⋅sin(37°)
Using sin(37°)≈35=0.6:
Fy=100⋅0.6=60N
Step 4: Calculate the normal force (N)
The normal force can be calculated using the equilibrium of vertical forces. The weight of the block is balanced by the normal force and the vertical component of the pulling force:
W=N+Fy
Substituting the values:
100=N+60
N=100−60=40N
Step 5: Calculate the maximum static friction force (f_s)
The maximum static friction force can be calculated using the formula:
fs=μ⋅N
Substituting the values:
fs=0.1⋅40=4N
Step 6: Determine the frictional force acting on the block
Since the pulling force's horizontal component (80 N) is greater than the maximum static friction force (4 N), the block will move. Therefore, the frictional force acting on the block will be equal to the maximum static friction force:
f=fs=4N
Final Answer
The frictional force acting on the body is 4 N.
---
- Mass of the block (m) = 10 kg
- Coefficient of friction (μ) = 0.1
- Pulling force (F) = 100 N
- Angle of pulling force (θ) = 37°
The weight (W) of the block can be calculated using the formula:
W=m⋅g
Where g (acceleration due to gravity) is approximately 10m/s2.
W=10kg⋅10m/s2=100N
The pulling force can be resolved into horizontal (F_x) and vertical (F_y) components:
- Horizontal component:
Fx=F⋅cos(θ)=100⋅cos(37°)
Using cos(37°)≈45=0.8:
Fx=100⋅0.8=80N
Fy=F⋅sin(θ)=100⋅sin(37°)
Using sin(37°)≈35=0.6:
Fy=100⋅0.6=60N
The normal force can be calculated using the equilibrium of vertical forces. The weight of the block is balanced by the normal force and the vertical component of the pulling force:
W=N+Fy
Substituting the values:
100=N+60
N=100−60=40N
The maximum static friction force can be calculated using the formula:
fs=μ⋅N
Substituting the values:
fs=0.1⋅40=4N
Since the pulling force's horizontal component (80 N) is greater than the maximum static friction force (4 N), the block will move. Therefore, the frictional force acting on the block will be equal to the maximum static friction force:
f=fs=4N
The frictional force acting on the body is 4 N.
Similar Questions
Knowledge Check
A block of mass 10kg is placed on a rough horizontal surface having coefficient of friction μ=0.5 . If a horizontal force of 100N is acting on it, then acceleration of the block will be.
A10ms−2B5ms−2C15ms−2D0.5ms−2
A block of mass 10kg is placed on a rough horizontal surface having coefficient of friction μ=0.5 . If a horizontal force of 100N is acting on it, then acceleration of the will be.
View SolutionA block of mass 10kg is placed on a rough horizontal surface having coefficient of friction μ=0.5 . If a horizontal force of 100N is acting on it, then acceleration of the block will be.
View SolutionA body of mass 2kg is placed on a horizontal surface having kinetic friction 0.4 and static friction 0.5 . If the force applied on the body is 2.5N , then the frictional force acting on the body will be
View SolutionA block of mass 4 kg is kept on a rough horizontal surface. The coefficient of static friction is 0.8. If a forace of 19 N is applied on the block parallel to the floor, then the force of friction between the block and floor is
View SolutionA block of weight 100N is lying on a rough horizontal surface. If coefficient of friction 1/√3. The least possible force that can move the block is
View SolutionIn the given situation disc and ring are connected with a string as shown in the figure. Both are placed on the rough surface of coefficient of friction μ. A force F is applied on the centre of disc horizontally. Then frictional force acting on the ring will be
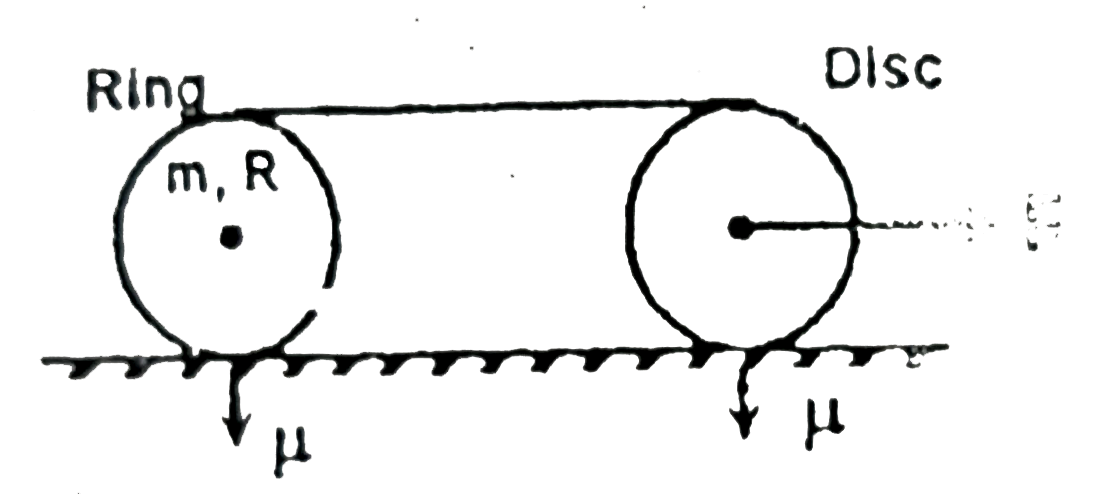
View SolutionA block of mass 10 kg is placed on the rough horizontal surface. A pulling force F is acting on the block which makes an angle θ above the horizontal. If coefficient of friction between block and surface is 43 then minimum value of force required to just move the block is (g=10ms2)
View Solution


