For 8g of helium gas (assume ideal behaviour), what is the slope of the straight line in PV VS T graph
1 lt. atm. K−1
0.0821 lt. atm. K−1
0.1642 lt. atm .K−1
2 lt. atm . K−1
The correct Answer is:C
To find the slope of the straight line in the PV vs T graph for 8g of helium gas, we can follow these steps:
1. Understand the Ideal Gas Law: The ideal gas law is given by the equation:
PV=nRT
where P is pressure, V is volume, n is the number of moles, R is the universal gas constant, and T is temperature.
2. Rearranging the Equation: We can rearrange the ideal gas law to express PV in terms of T:
PV=nRT
This implies that if we plot PV on the y-axis and T on the x-axis, the slope of the line will be:
slope=PVT=nR
3. Calculate the Number of Moles (n): The number of moles can be calculated using the formula:
n=massmolar mass
For helium, the molar mass is 4 g/mol. Given that the mass of helium is 8 g:
n=8g4g/mol=2mol
4. Use the Universal Gas Constant (R): The value of the universal gas constant R in liter-atm per mole per Kelvin is:
R=0.0821L atm/(mol K)
5. Calculate the Slope: Now, substituting the values of n and R into the slope formula:
slope=nR=2mol×0.0821L atm/(mol K)=0.1642L atm/K
6. Final Answer: Therefore, the slope of the straight line in the PV vs T graph for 8 g of helium gas is:
slope=0.1642L atm/K
Conclusion:
The correct answer is 0.1642L atm/K.
PV=nRT
where P is pressure, V is volume, n is the number of moles, R is the universal gas constant, and T is temperature.
PV=nRT
This implies that if we plot PV on the y-axis and T on the x-axis, the slope of the line will be:
slope=PVT=nR
n=massmolar mass
For helium, the molar mass is 4 g/mol. Given that the mass of helium is 8 g:
n=8g4g/mol=2mol
R=0.0821L atm/(mol K)
slope=nR=2mol×0.0821L atm/(mol K)=0.1642L atm/K
slope=0.1642L atm/K
The correct answer is 0.1642L atm/K.
Similar Questions
What is the slope of x-t graph of a stationary object?
View SolutionLine t is shown in the xy-plane below
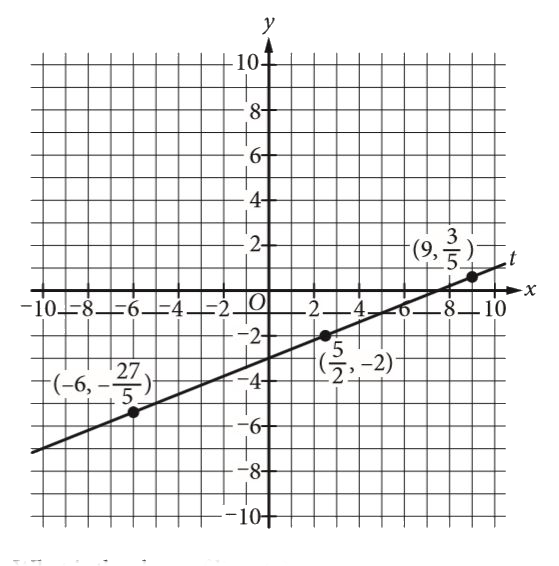
What is the slope of line t ?
View SolutionIf a graph is plotted between log(a−x) and t, the slope of the straight line is equal to −0.03. The specific reaction rate will be
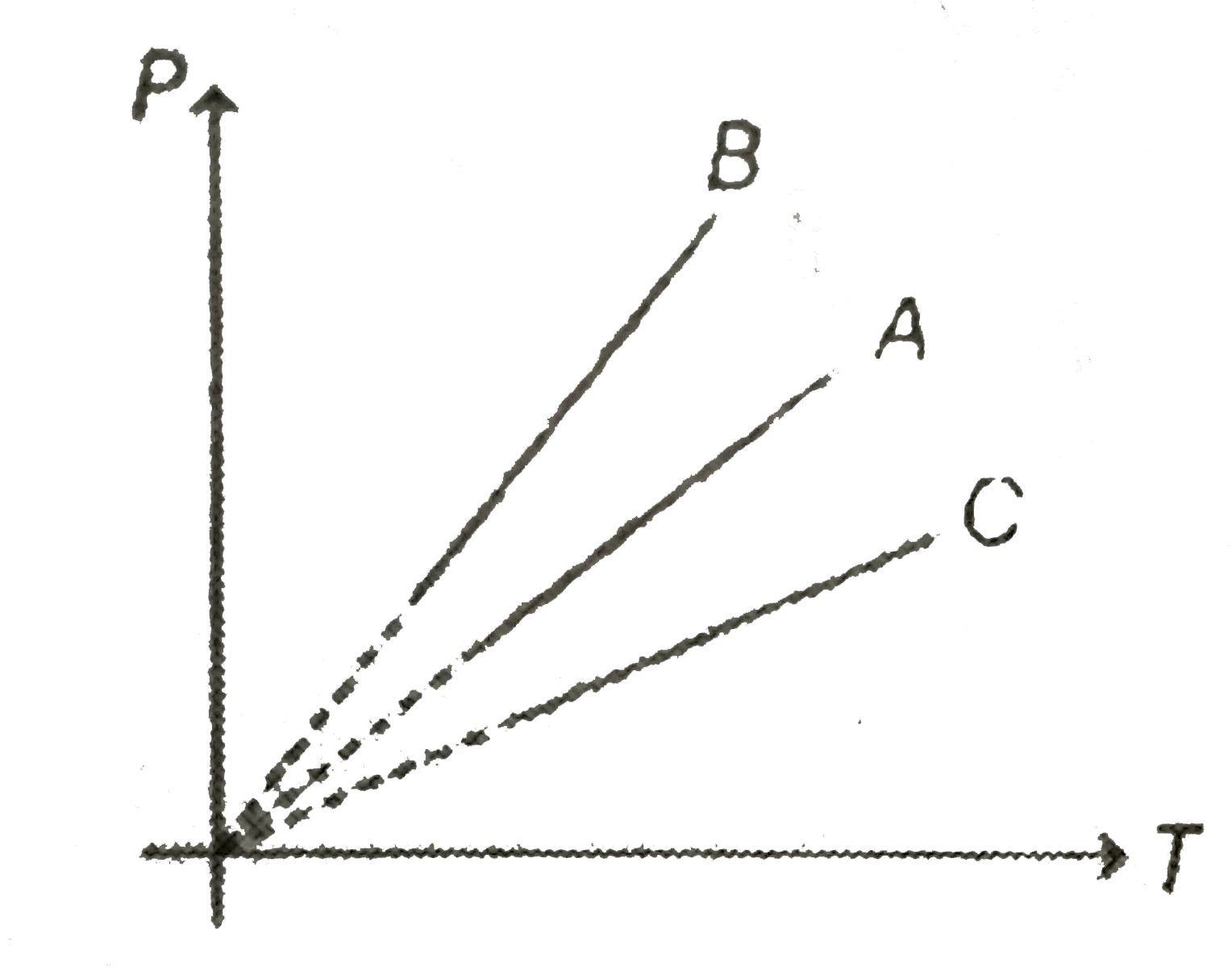
View SolutionPressure versus temperature graph of an ideal gas at constant volume V is shown by the straight line A. Now mass of the gas is doubled and the volume is halved, then the corresponding pressure versus temperature graph will be shown by the line
View SolutionConsider the following figure at 500 K.Assuming ideal gas behaviour, calculate the total pressure if the barriers are removed from the compartment.Assume that the volume of barriers is negligible.

View SolutionThe expansion of an ideal gas of mass m at a constant pressure P is given by the straight line D. Then the expanison of the same ideal gas of mass 2m at a pressure P/2 is given by the straight line

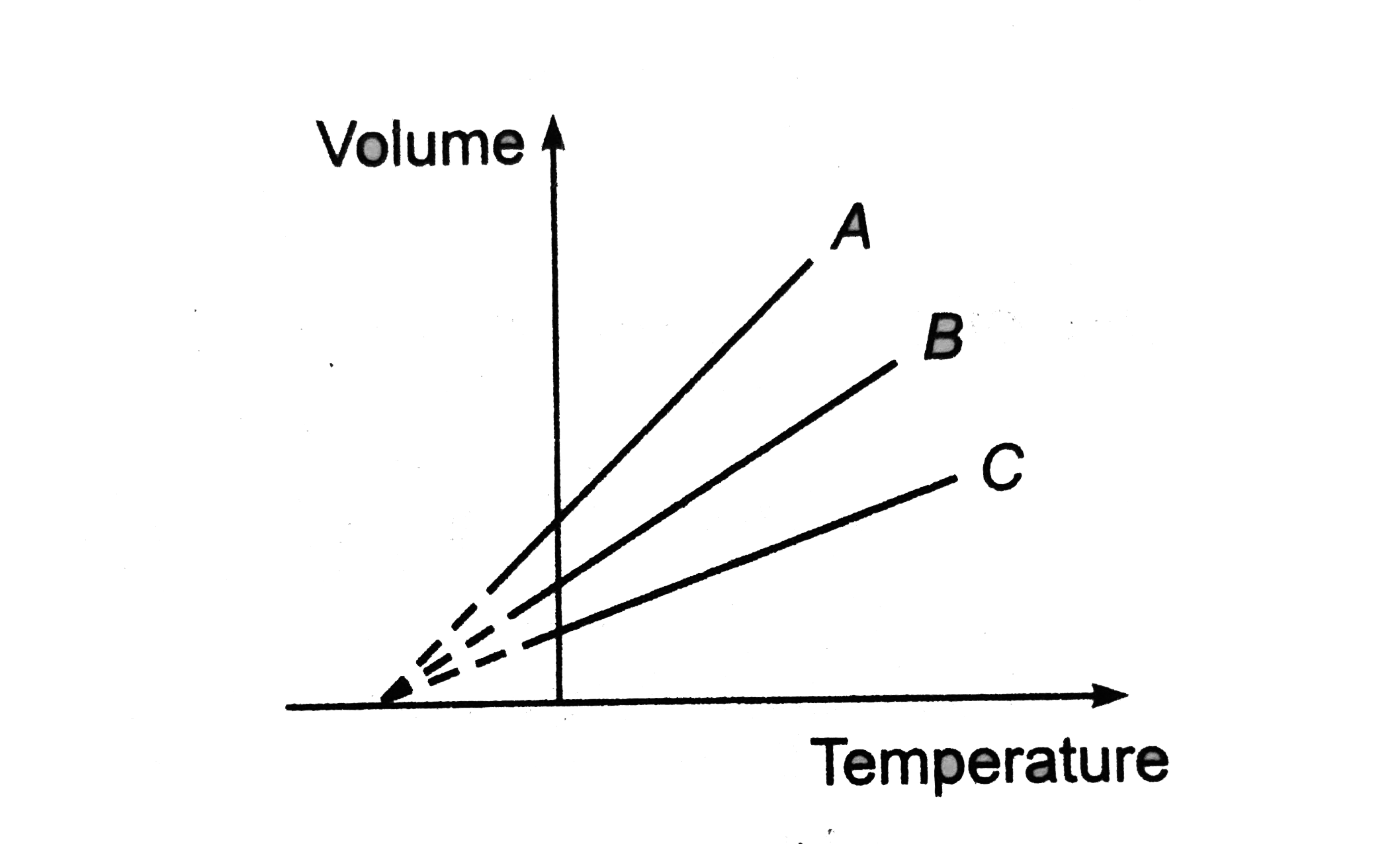
View SolutionThe expansion of an ideal gas of mass (m) at a constant pressure (p) is given by the straight line (B) Then, the expansion of the same ideal gas of mass 2m at a pressure 2p is given by the straight line.
 .
.
View SolutionFor an ideal gas which of the following graphs will not be straight line when all the other variables are held constant?
View SolutionA high altitude balloon contains 6.81 g of helium in 1.16×104 L at−23∘C. Assuming ideal gas behaviour, how many grams of helium would have to be added to increase the pressure to 4.0×10−3 atm?
View SolutionWhen 2g of a gas A is introduced into an evacuated flask kept at 25∘C, the pressure is found to be one atmosphere. If 3 g of another gas B are then added to the same flask, the total pressure becomes 1.5 atm. Assuming ideal gas behaviour, calculate the ratio of molecular weights MA:MB.
View Solution
