H2O21storder−−−−→H2O+12O2. Pressure of O2 is recorded as:
time (min) 10 min ∝
PO2 (mm) 120 160
What is half life?
The correct Answer is:5
To find the half-life of the reaction H2O2→H2O+12O2 given the pressure of O2 at different times, we can follow these steps:
Step 1: Understand the Reaction and Given Data
The reaction is a first-order reaction, and we are given the pressure of O2 at two different times:
- At t=10 minutes, P(O2)=120 mm
- At t→∞, P(O2)=160 mm
Step 2: Determine the Change in Pressure
The change in pressure of O2 from the initial state to the state at t=10 minutes can be calculated as follows:
- Initial pressure of O2 (at t=∞) = 160 mm
- Pressure of O2 after 10 minutes = 120 mm
- Therefore, the amount of O2 produced in 10 minutes = 160−120=40 mm
Step 3: Use the First-Order Kinetics Equation
For a first-order reaction, the rate constant k can be calculated using the formula:
k=2.303tlog(A0At)
Where:
- A0 = initial amount (pressure at t=∞) = 160 mm
- At = amount at time t (pressure at t=10 min) = 120 mm
- t = time = 10 min
Substituting the values:
k=2.30310log(160120)
Step 4: Calculate the Logarithm
Calculate 160120=43:
log(43)≈0.1249
Now substituting this back into the equation for k:
k=2.30310×0.1249≈0.0288 min−1
Step 5: Calculate the Half-Life
The half-life t1/2 for a first-order reaction is given by:
t1/2=0.693k
Substituting the value of k:
t1/2=0.6930.0288≈24.1 minutes
Final Answer
The half-life of the reaction is approximately 24.1 minutes.
The reaction is a first-order reaction, and we are given the pressure of O2 at two different times:
- At t=10 minutes, P(O2)=120 mm
- At t→∞, P(O2)=160 mm
The change in pressure of O2 from the initial state to the state at t=10 minutes can be calculated as follows:
- Initial pressure of O2 (at t=∞) = 160 mm
- Pressure of O2 after 10 minutes = 120 mm
- Therefore, the amount of O2 produced in 10 minutes = 160−120=40 mm
For a first-order reaction, the rate constant k can be calculated using the formula:
k=2.303tlog(A0At)
Where:
- A0 = initial amount (pressure at t=∞) = 160 mm
- At = amount at time t (pressure at t=10 min) = 120 mm
- t = time = 10 min
k=2.30310log(160120)
Calculate 160120=43:
log(43)≈0.1249
Now substituting this back into the equation for k:
k=2.30310×0.1249≈0.0288 min−1
The half-life t1/2 for a first-order reaction is given by:
t1/2=0.693k
Substituting the value of k:
t1/2=0.6930.0288≈24.1 minutes
The half-life of the reaction is approximately 24.1 minutes.
Similar Questions
H2O2R.T.−−→H2O+12O2
View SolutionH2O2R.T.−−→H2O+12O2
View Solution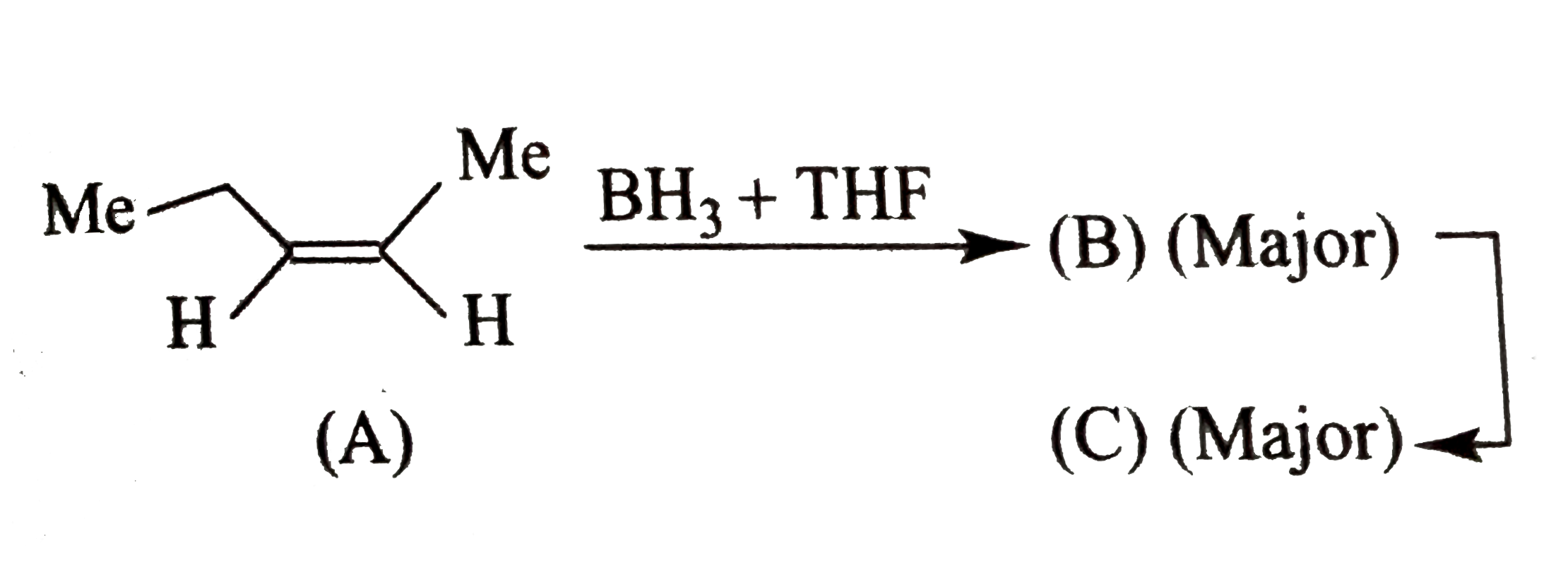 H2O2+ΘOH
H2O2+ΘOH
B and C are:
View SolutionH2OandH2O2 resemble in
View SolutionH2O2→H2O+12O2 equivalent mass of H2O2 is
View SolutionH2O2→H2O+O2
This represents
View SolutionNH3+O2Pt−−→ΔA+H2O
A+O2→B,
B+O2+H2O→C
A, B and C are:
View SolutionNH3+O2Pt−−→ΔA+H2O
A+O2→B,
B+O2+H2O→C
A, B and C are:
View Solution1 ml of H2O2 solution given 10 ml of O2 at NTP. It is :
View SolutionCompare the stuctures of H2O and H2O2.
View Solution