Suppose a population A has 100 observations 101, 102,… 200, and another population B has 100 observations 151, 152,…250. If VA and VB represent the variances of the two populations respectively, then show that VAVB=1
To solve the problem, we need to calculate the variances VA and VB for the two populations A and B, and then show that the ratio VAVB=1.
Step 1: Define the populations
- Population A consists of 100 observations: 101,102,…,200.
- Population B consists of 100 observations: 151,152,…,250.
Step 2: Calculate the mean of each population
- For Population A:
Mean of A=101+2002=3012=150.5
- For Population B:
Mean of B=151+2502=4012=200.5
Step 3: Calculate the variance for each population
The formula for variance V is given by:
V=∑(xi−¯x)2n
where xi are the observations, ¯x is the mean, and n is the number of observations.
Variance of Population A:
1. Calculate ∑(xi−¯x)2 for Population A:
∑(xi−150.5)2=200∑i=101(i−150.5)2
This can be calculated as:
=200∑i=101(i2−2⋅150.5⋅i+(150.5)2)
The sum of squares 200∑i=101i2 can be calculated using the formula for the sum of squares of the first n natural numbers.
2. The variance VA is then:
VA=∑(xi−150.5)2100
Variance of Population B:
1. Calculate ∑(xi−¯x)2 for Population B:
∑(xi−200.5)2=250∑i=151(i−200.5)2
Similar to Population A, this can be calculated as:
=250∑i=151(i2−2⋅200.5⋅i+(200.5)2)
2. The variance VB is then:
VB=∑(xi−200.5)2100
Step 4: Show that VAVB=1
Since both populations consist of consecutive integers, the spread of the values around their respective means is the same. Therefore, the sums of squares around their means will yield the same result, leading to:
VAVB=1
Conclusion
Thus, we have shown that:
VAVB=1
- Population A consists of 100 observations: 101,102,…,200.
- Population B consists of 100 observations: 151,152,…,250.
- For Population A:
Mean of A=101+2002=3012=150.5
Mean of B=151+2502=4012=200.5
The formula for variance V is given by:
V=∑(xi−¯x)2n
where xi are the observations, ¯x is the mean, and n is the number of observations.
1. Calculate ∑(xi−¯x)2 for Population A:
∑(xi−150.5)2=200∑i=101(i−150.5)2
This can be calculated as:
=200∑i=101(i2−2⋅150.5⋅i+(150.5)2)
The sum of squares 200∑i=101i2 can be calculated using the formula for the sum of squares of the first n natural numbers.
VA=∑(xi−150.5)2100
1. Calculate ∑(xi−¯x)2 for Population B:
∑(xi−200.5)2=250∑i=151(i−200.5)2
Similar to Population A, this can be calculated as:
=250∑i=151(i2−2⋅200.5⋅i+(200.5)2)
VB=∑(xi−200.5)2100
Since both populations consist of consecutive integers, the spread of the values around their respective means is the same. Therefore, the sums of squares around their means will yield the same result, leading to:
VAVB=1
Thus, we have shown that:
VAVB=1
Similar Questions
Suppose a population A has 100 observations 101,102,................,200 and another population B has 100 observations 151,152,........250. If VAandVB represent the variances of the two populations respectively, then VAVB is
View SolutionOne set of 100 observations has the mean 15 and another set of 150 observation has the mean 16. Find the mean of 250 observation by combining the two sets of given observations.
View Solution
Knowledge Check
A circuit has a section ABC if the potential at point A,BandC are V1,V2andV3 respectively , calculate the potential at point O
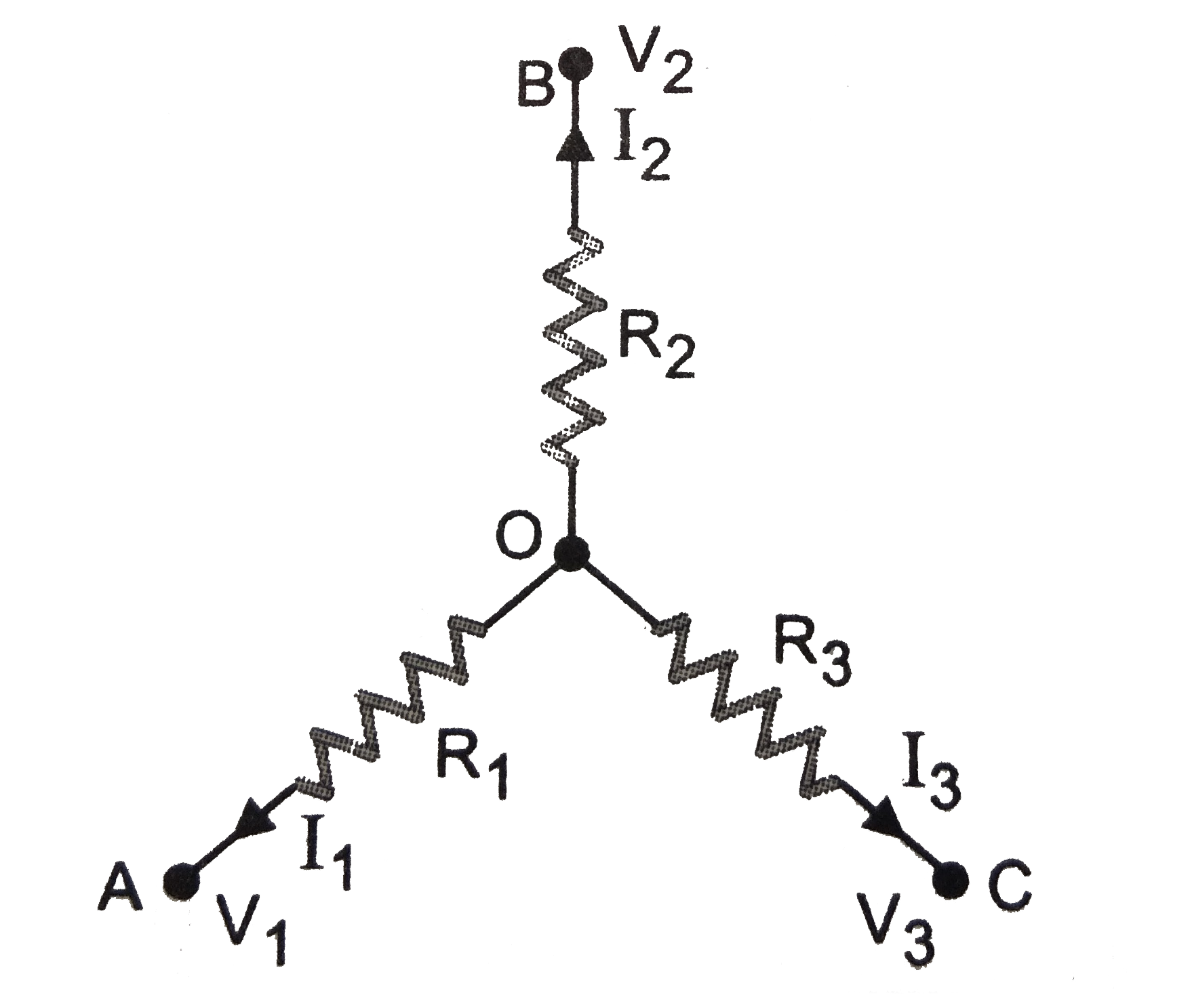 AV1+V2+V3B[V1+V2+V3R1+R2+R3][1R1+R2+R3]−1CzeroD[V1+V2+V3R1+R2+R3](R1+R2+R3)
AV1+V2+V3B[V1+V2+V3R1+R2+R3][1R1+R2+R3]−1CzeroD[V1+V2+V3R1+R2+R3](R1+R2+R3)
Two particles of mass mA and mB and their velocities are VA and VB respectively collides. After collision they interchanges their velocities, then ratio of mAmB is
View SolutionIf a ,b,c, and u,v,w are complex numbers representing the vertices of two triangle such that they are similar, then prove that a−ca−b=u−wu−v
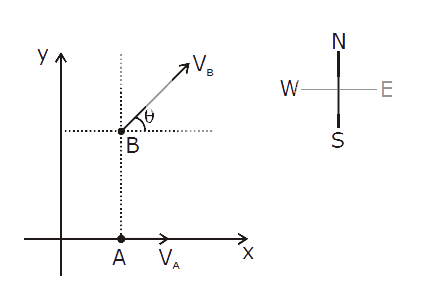
View SolutionFigure shows two ships moving in x-y plane with velocity VA and VB . The ships move such that B always
remains north of A . The ratio VAVB is eqal to -
View SolutionTwo objects A and B are moving in opposite directions with velocities vAandvB respectively, the magnitude of relative velocity of A w.r.t. B is
View SolutionTwo bulbs B_1 and B_2 with ratings (10W, 220V) and (20 W, 220V) respectively are connected in parallel across a 440V input supply. Then
View SolutionTwo elements A and B with atomic numbers ZA and ZB are used to produce charateristic X-rays with frequencies vA and vB respectively. If ZA:ZB=1:2, then vA:vB will be
View SolutionIf variance of ten observations 10,20,30,40,50,....100 is A and variance of ten another observations 22,42,62,82,102,...202 is B, then BA is 1. 0 2. 1 3. 2 4. 3 5. 4
View Solution
