The range of a random variable X is {0, 1, 2}. Given that P(X=0)=3c3,P(X=1)=4c−10c2,P(X=2)=5c−1 where c is constant.
Find (i) the value of c (ii) P(X<1)
(iii) P(1<X≤2) (iv) P(0<X≤3)
The correct Answer is:i) 13 ii) 19 iii) 23 iv) 89
To solve the problem step by step, we will follow the instructions provided in the video transcript.
Step 1: Find the value of c
We know that the sum of the probabilities must equal 1:
P(X=0)+P(X=1)+P(X=2)=1
Substituting the given probabilities:
3c3+(4c−10c2)+(5c−1)=1
Combining like terms:
3c3−10c2+9c−2=0
Now we need to find the roots of this cubic equation. We can test possible rational roots.
Testing c=1:
3(1)3−10(1)2+9(1)−2=3−10+9−2=0
Thus, c=1 is a root. We can factor the cubic polynomial using c−1.
Using synthetic division or polynomial long division, we divide 3c3−10c2+9c−2 by c−1:
The result of the division is:
3c2−7c+2
Now we can find the roots of the quadratic equation 3c2−7c+2=0 using the quadratic formula:
c=−b±√b2−4ac2a
Substituting a=3,b=−7,c=2:
c=7±√(−7)2−4⋅3⋅22⋅3=7±√49−246=7±√256=7±56
Calculating the two possible values:
1. c=126=2
2. c=26=13
Now we need to check which values of c give valid probabilities.
- For c=1: P(X=1)=4(1)−10(12)=4−10=−6 (not valid)
- For c=2: P(X=1)=4(2)−10(22)=8−40=−32 (not valid)
- For c=13:
P(X=1)=4(13)−10(13)2=43−109=129−109=29(valid)
Thus, the only valid value for c is:
13
Step 2: Find P(X<1)
Since P(X<1)=P(X=0):
P(X=0)=3c3=3(13)3=3⋅127=19
Thus,
19
Step 3: Find P(1<X≤2)
This is equal to P(X=2):
P(X=2)=5c−1=5(13)−1=53−1=53−33=23
Thus,
23
Step 4: Find P(0<X≤3)
Since X can only take values 0, 1, and 2, we have:
P(0<X≤3)=P(X=1)+P(X=2)
Calculating P(X=1):
P(X=1)=4c−10c2=4(13)−10(13)2=43−109=129−109=29
Now adding P(X=2):
P(0<X≤3)=P(X=1)+P(X=2)=29+23=29+69=89
Thus,
89
Summary of Answers
1. c=13
2. P(X<1)=19
3. P(1<X≤2)=23
4. P(0<X≤3)=89
2. c=26=13
- For c=2: P(X=1)=4(2)−10(22)=8−40=−32 (not valid)
- For c=13:
1. c=13
2. P(X<1)=19
3. P(1<X≤2)=23
4. P(0<X≤3)=89
Similar Questions
A random variable x had its range {0, 1, 2} and the probabilities are given by P(x=0)=3k3,P(x=1)=4k−10k2,P(x=2)=5k−1 where k is constant then k =
View SolutionThe random variable X can take only the values 0, 1, 2. Given that P(X=0) = P(X= 1) = p and E(X2)=E(X) , then find the value of p
View SolutionThe random variable X can take only the values 0,1,2. Given that P(X=0)=P(X=1)=p and that E(X2)=E(X); find the value of p.
View SolutionThe range of a random variable X is {1, 2, 3, ……..} and P(X=k)=Ck⌊k where k = 1, 2, 3,…. Find the value of C
View SolutionThe probability of a random variable X is given below
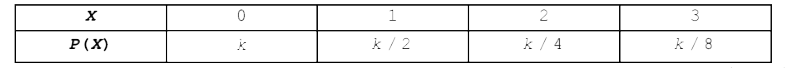
Find P(X≤2)+P(X>2)
View SolutionThe probability distribution function of a random variable X is given by xi:012 pi:3c34c−10c25c−1 Where c>0. Find : (i) c (ii) P(X<2) (iii) P(1<X≤2).
View SolutionA random variable X takes the values 0,1,2,3,..., with prbability PX(=x)=k(x+1)(15)x, where k is a constant, then P(X=0) is.
View SolutionThe random variable X can the values 0, 1, 2, 3, Give P(X = 0) = P(X = 1)= p and P(X = 2) = P(X = 3) such that ∑pix2i=2∑pixi then find the value of p
View SolutionThe range of random variable x={1,2,3….} and the probabilities are given by P(x=k)=3CKK! (k = 1, 2, 3, ……) and C is a constant. Then C =
View SolutionThe probability distribution of a random variable x is given as under
P(X=x)=⎧⎪⎨⎪⎩kx2x=1,2,32kxx=4,5,60,otherwise
where, k is a constant. Calculate
(i) E(X) (ii) E(3X2) (iii) P(X≥4)
View Solution

