A body is sliding down an inclined plane having coefficient of friction 0.5. If the normal reaction is twice that of the resultant downward force along the inclination the angle between the inclined plane and the horizontal is
To solve the problem step by step, we will analyze the forces acting on the body sliding down the inclined plane and apply the conditions given in the question.
Step 1: Identify the forces acting on the body
- The weight of the body W=mg acts vertically downwards.
- The component of the weight acting parallel to the inclined plane is W∥=mgsinθ.
- The component of the weight acting perpendicular to the inclined plane is W_{\perpendicular} = mg \cos \theta .
- The normal force N acts perpendicular to the inclined plane.
- The frictional force Ff opposes the motion and is given by Ff=μN=0.5N.
Step 2: Set up the equations based on the problem statement
According to the problem, the normal reaction N is twice the resultant downward force along the inclination. Therefore, we can write:
N=2Fresultant
Where Fresultant is the net force acting down the incline. The net force down the incline can be expressed as:
Fresultant=mgsinθ−Ff
Substituting the expression for frictional force:
Fresultant=mgsinθ−0.5N
Step 3: Substitute N in terms of Fresultant
From the previous equation, substituting N:
N=2(mgsinθ−0.5N)
Expanding this gives:
N=2mgsinθ−N
Adding N to both sides:
2N=2mgsinθ
Thus, we find:
N=mgsinθ
Step 4: Relate normal force to the weight component
We also know from the forces acting perpendicular to the incline that:
N=mgcosθ
Now we have two expressions for N:
1. N=mgsinθ
2. N=mgcosθ
Step 5: Set the equations for N equal to each other
Setting the two expressions for N equal gives:
mgsinθ=mgcosθ
Dividing both sides by mg (assuming m≠0 and g≠0):
sinθ=cosθ
Step 6: Solve for θ
From sinθ=cosθ, we can divide both sides by cosθ:
tanθ=1
Thus, we find:
θ=tan−1(1)
This implies:
θ=45∘
Conclusion
The angle between the inclined plane and the horizontal is 45∘.
- The weight of the body W=mg acts vertically downwards.
- The component of the weight acting parallel to the inclined plane is W∥=mgsinθ.
- The component of the weight acting perpendicular to the inclined plane is W_{\perpendicular} = mg \cos \theta .
- The normal force N acts perpendicular to the inclined plane.
- The frictional force Ff opposes the motion and is given by Ff=μN=0.5N.
According to the problem, the normal reaction N is twice the resultant downward force along the inclination. Therefore, we can write:
N=2Fresultant
Where Fresultant is the net force acting down the incline. The net force down the incline can be expressed as:
Fresultant=mgsinθ−Ff
Substituting the expression for frictional force:
Fresultant=mgsinθ−0.5N
From the previous equation, substituting N:
N=2(mgsinθ−0.5N)
Expanding this gives:
N=2mgsinθ−N
Adding N to both sides:
2N=2mgsinθ
Thus, we find:
N=mgsinθ
We also know from the forces acting perpendicular to the incline that:
N=mgcosθ
Now we have two expressions for N:
1. N=mgsinθ
2. N=mgcosθ
Setting the two expressions for N equal gives:
mgsinθ=mgcosθ
Dividing both sides by mg (assuming m≠0 and g≠0):
sinθ=cosθ
From sinθ=cosθ, we can divide both sides by cosθ:
tanθ=1
Thus, we find:
θ=tan−1(1)
This implies:
θ=45∘
The angle between the inclined plane and the horizontal is 45∘.
Similar Questions
A body is sliding down an inclined plane having coefficient of friction 1/3. If the normal reaction is three times that of the resultant downward force along the incline, the angle between the inclined plane and the horizontal is
View SolutionWhen a body slides down an inclined plane with coefficient of friction as μk, then its acceleration is given by .
View Solution
Knowledge Check
A block of mass m rests on a rough inclined plane. The coefficient of friction between the surface and the block is µ. At what angle of inclination θ of the plane to the horizontal will the block just start to slide down the plane?
Aθ=tan−1μBθ=cos−1μCθ=sin−1μDθ=sec−1μ
When a body of mass M slides down an inclined plane of inclination θ, having coefficient of friction μ through a distance s, the work done against friction is :
View SolutionA body is placed on an inclined plane and has to be pushed down. The angle made by the normal reaction with the vertical will be:-
View SolutionA block slides down on inclined plane (angle of inclination 60∘ ) with an accelration g/2 Find the coefficient friction

View SolutionA rectangular box lies on a rough inclined surface . The coefficient of friction between the surface and the box is μ. Let the mass of the box be m .
(a) At what angle of inclination θ of the plane to the horizontal will the box just start to slide down the plane ?
(b) What is the force acting on the box down the plane , if the angle of inclination of the plane is increased to α>θ ?
(c) What is the force needed to be applied upwards along the plane to make the box either remain stationary or just move up with uniform speed ?
(d) What is the force needed to be applied upwards along the plane to make the box move up the plane with acceleration a ?
View SolutionAssertion: A body slides down an inclined plane if the angle of friction is more than the angle of the inclined plane with the horizontal.
Reason : When the angle of inclination is equal to the angle of friction, the component of weight parallel to the plane is just sufficient to overcome the frictional force.
View SolutionThe value of angle such that the acceleration of A is g/6 downwards along the incline plane.
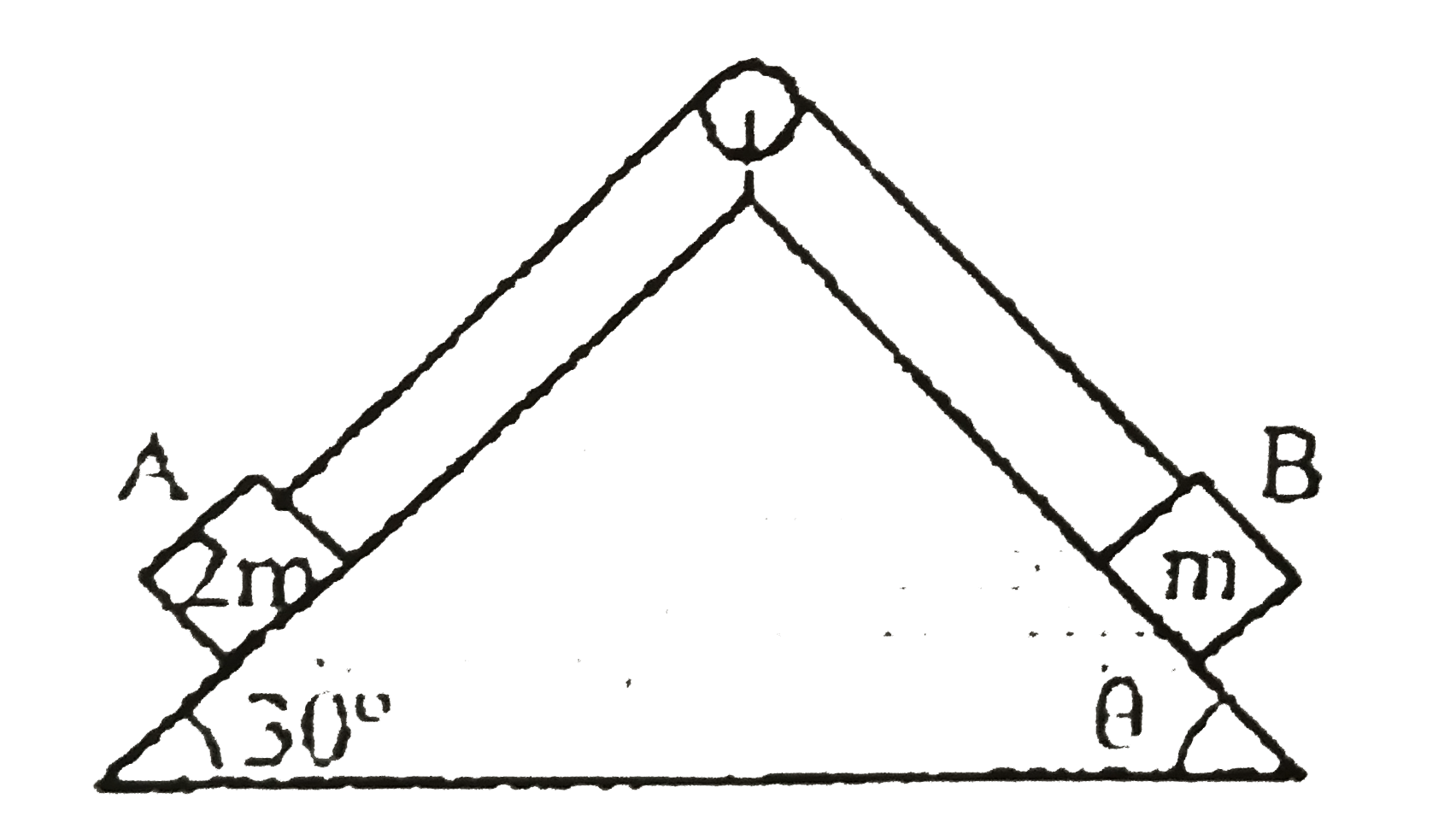
View Solution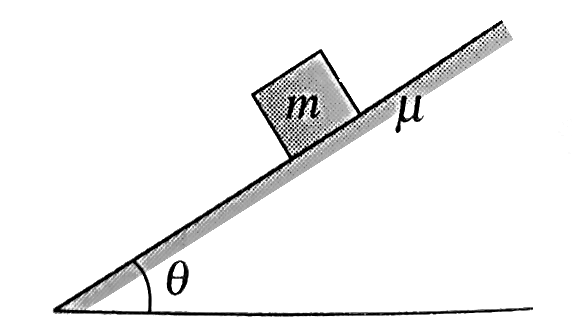 A block of mass m is placed on a rough inclined plane. The corfficient of friction between the block and the plane is μ and the inclination of the plane is θ.Initially θ=0 and the block will remain stationary on the plane. Now the inclination θ is gradually increased . The block presses theinclined plane with a force mgcosθ. So welding strength between the block and inclined is μmgcosθ, and the pulling forces is mgsinθ. As soon as the pulling force is greater than the welding strength, the welding breaks and the blocks starts sliding, the angle θ for which the block start sliding is called angle of repose (λ). During the contact, two contact forces are acting between the block and the inclined plane. The pressing reaction (Normal reaction) and the shear reaction (frictional force). The net contact force will be resultant of both.
A block of mass m is placed on a rough inclined plane. The corfficient of friction between the block and the plane is μ and the inclination of the plane is θ.Initially θ=0 and the block will remain stationary on the plane. Now the inclination θ is gradually increased . The block presses theinclined plane with a force mgcosθ. So welding strength between the block and inclined is μmgcosθ, and the pulling forces is mgsinθ. As soon as the pulling force is greater than the welding strength, the welding breaks and the blocks starts sliding, the angle θ for which the block start sliding is called angle of repose (λ). During the contact, two contact forces are acting between the block and the inclined plane. The pressing reaction (Normal reaction) and the shear reaction (frictional force). The net contact force will be resultant of both.
Answer the following questions based on above comprehension:
Q. If μ=34 then what will be frictional force (shear force) acting between the block and inclined plane when θ=30∘:
View Solution