Two blocks A and B of masses 2kg and 3kg are connected by a light string as shown in the figure and placed on a horizontal surface. μ between all surfaces is 0.1 and g = 10ms−1. The acceleration of the system is, when the force applied F = 45N
To solve the problem, we need to find the acceleration of the system consisting of two blocks A and B connected by a light string when a force of 45 N is applied. The coefficients of friction and the masses of the blocks are also given.
1. Identify the masses and coefficients:
- Mass of block A (m1) = 2 kg
- Mass of block B (m2) = 3 kg
- Coefficient of friction (μ) = 0.1
- Acceleration due to gravity (g) = 10 m/s²
- Applied force (F) = 45 N
2. Calculate the normal force (N):
The normal force for both blocks combined is equal to their total weight:
N=(m1+m2)⋅g=(2kg+3kg)⋅10m/s²=5kg⋅10m/s²=50N
3. Calculate the frictional force (f):
The frictional force opposing the motion is given by:
f=μ⋅N=0.1⋅50N=5N
4. Determine the net force (F_net) acting on the system:
The net force is the applied force minus the frictional force:
Fnet=F−f=45N−5N=40N
5. Calculate the total mass (M) of the system:
M=m1+m2=2kg+3kg=5kg
6. Use Newton's second law to find the acceleration (a):
According to Newton's second law:
Fnet=M⋅a
Rearranging gives:
a=FnetM=40N5kg=8m/s²
Final Answer:
The acceleration of the system is 8m/s².
---
- Mass of block A (m1) = 2 kg
- Mass of block B (m2) = 3 kg
- Coefficient of friction (μ) = 0.1
- Acceleration due to gravity (g) = 10 m/s²
- Applied force (F) = 45 N
The normal force for both blocks combined is equal to their total weight:
N=(m1+m2)⋅g=(2kg+3kg)⋅10m/s²=5kg⋅10m/s²=50N
The frictional force opposing the motion is given by:
f=μ⋅N=0.1⋅50N=5N
The net force is the applied force minus the frictional force:
Fnet=F−f=45N−5N=40N
M=m1+m2=2kg+3kg=5kg
According to Newton's second law:
Fnet=M⋅a
Rearranging gives:
a=FnetM=40N5kg=8m/s²
The acceleration of the system is 8m/s².
Similar Questions
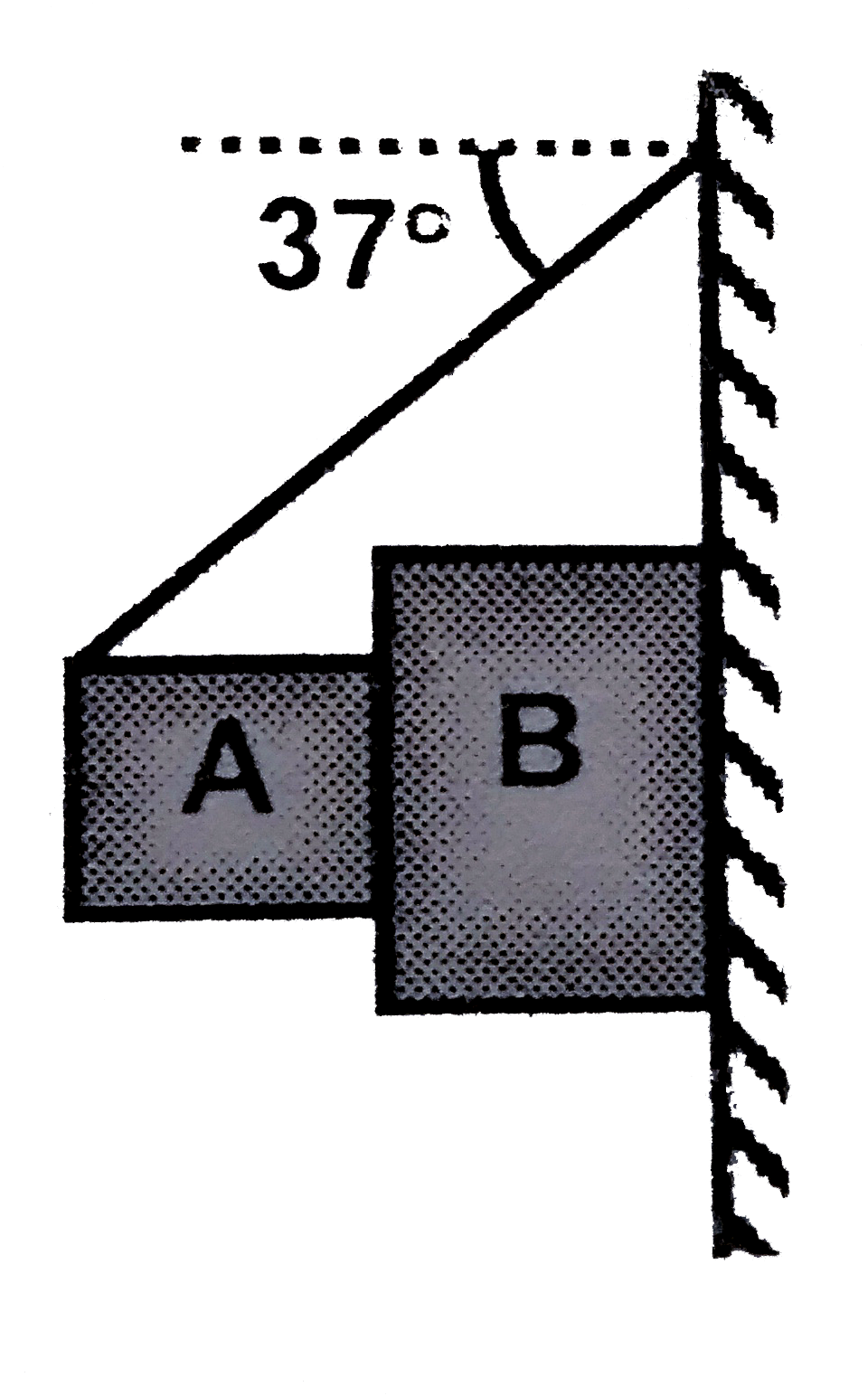
Two block A and B of mass 50kg and 300kg respectively are placed as shown in figure. Coefficient of friction between all surface is 12
Then (take g=10m/s)
View SolutionTwo blocks A and B of masses m and M are attached with ideal string and pulley, and placed on smooth horizontal surface. Force F is applied horizontally as shown in figure. Find the ratio of the acceleration of A to that of B.

View Solution
Knowledge Check
Two blocks of masses 10 kg and 20 kg are connected by a massless string and are placed on a smooth horizontal surface as shown in the figure. If a force F=600 N is applied to 10 kg block, then the tension in the string is
 A100NB200NC300ND400N
A100NB200NC300ND400N
Two blocks of mass 4kg and 6kg are connected by a string as shown in the figure. They are initially at rest on the floor. Calculate their acceleration when a force of (a) 50N (b) 100N is applied on the pulley.
View SolutionTwo blocks of masses 7 kg and 3 kg are connected by a spring of stiffness 1000Nm−1 and placed on a smooth horizontal surface. They are acted by horizontal forces of 72 N and 32 N in opposite directions as shown in the figure. When accelerations of the blocks are equal and constant, the extension of the spring is
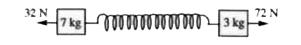
View SolutionTwo block of mass 1kg and 2kg are connected by a string AB of mass 1kg. The blocks are placed on a smooth horizontal surface. Block of mass 1kg is pulled by a horizontal force F of magnitude 8N. Find the tension in the string at points A and B

View SolutionTwo blocks of masses 4kg and 2kg are placed side on a smooth horizontal surface as shown in the figure. A horizontal force of 20N is applied on 4kgblock. Find
(a) the acceleration of each block.
(b) the normal reaction between two blocks.

View SolutionTwo blocks of masses 4kg and 2kg are placed side on a smooth horizontal surface as shown in the figure. A horizontal force of 20N is applied on 4kgblock. Find
(a) the acceleration of each block.
(b) the normal reaction between two blocks.

View SolutionTwo block of mass 4 kg and 2 kg are attached by an inextensible light string as shown in figure. Both the blocks are pulled vertically upwards by a force F=120N
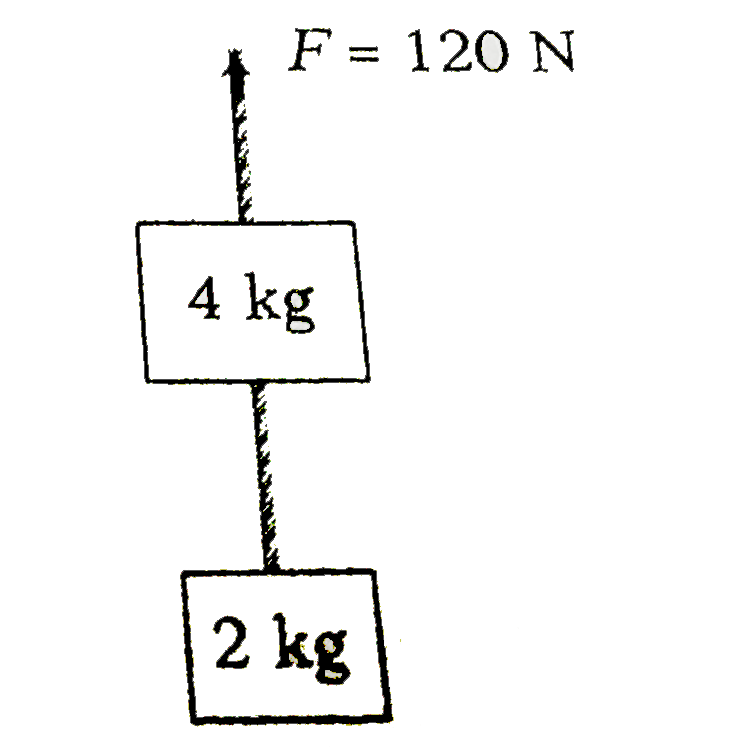
Find
(a) the acceleration of the blocks,
(b) tension in the string. (Take g=10ms−2)
View SolutionTwo block of mass 4 kg and 2 kg are attached by an inextensible light string as shown in figure. Both the blocks are pulled vertically upwards by a force F=120N
Find
(a) the acceleration of the blocks
(b) tension in the string. (Take g=10ms−2)

View Solution
