A body of mass 60 kg is pushed up with just enough force to start it moving on a rough surface with and and the force continues to act afterwards. What is the acceleration of the body ?
To solve the problem step by step, we can follow these procedures:
Step 1: Identify the forces acting on the body
When the body is at rest and is about to start moving, the force applied must overcome the static friction. Once it starts moving, the kinetic friction will act against the applied force.
Step 2: Calculate the normal force
The normal force (N) acting on the body is equal to its weight when it is on a horizontal surface. The weight can be calculated using the formula:
N=m⋅g
Where:
- m=60kg (mass of the body)
- g=9.8m/s2 (acceleration due to gravity)
So,
N=60kg⋅9.8m/s2=588N
Step 3: Calculate the static friction force
The maximum static friction force (Fs) that needs to be overcome to start moving the body can be calculated using the coefficient of static friction (μs):
Fs=μs⋅N
Where μs=0.5.
So,
Fs=0.5⋅588N=294N
Step 4: Calculate the kinetic friction force
Once the body is in motion, the kinetic friction force (Fk) acting on the body can be calculated using the coefficient of kinetic friction (μk):
Fk=μk⋅N
Where μk=0.4.
So,
Fk=0.4⋅588N=235.2N
Step 5: Determine the net force acting on the body
The net force (Fnet) acting on the body after it starts moving is given by the difference between the applied force and the kinetic friction force:
Fnet=Fa−Fk
Since the applied force Fa is equal to the maximum static friction force when the body starts moving, we can substitute:
Fnet=294N−235.2N=58.8N
Step 6: Calculate the acceleration of the body
Using Newton's second law, the acceleration (a) can be calculated as:
Fnet=m⋅a
Rearranging gives:
a=Fnetm
Substituting the values:
a=58.8N60kg=0.98m/s2
Final Answer:
The acceleration of the body is 0.98m/s2.
---
When the body is at rest and is about to start moving, the force applied must overcome the static friction. Once it starts moving, the kinetic friction will act against the applied force.
The normal force (N) acting on the body is equal to its weight when it is on a horizontal surface. The weight can be calculated using the formula:
N=m⋅g
Where:
- m=60kg (mass of the body)
- g=9.8m/s2 (acceleration due to gravity)
N=60kg⋅9.8m/s2=588N
The maximum static friction force (Fs) that needs to be overcome to start moving the body can be calculated using the coefficient of static friction (μs):
Fs=μs⋅N
Where μs=0.5.
Fs=0.5⋅588N=294N
Once the body is in motion, the kinetic friction force (Fk) acting on the body can be calculated using the coefficient of kinetic friction (μk):
Fk=μk⋅N
Where μk=0.4.
Fk=0.4⋅588N=235.2N
The net force (Fnet) acting on the body after it starts moving is given by the difference between the applied force and the kinetic friction force:
Fnet=Fa−Fk
Since the applied force Fa is equal to the maximum static friction force when the body starts moving, we can substitute:
Fnet=294N−235.2N=58.8N
Using Newton's second law, the acceleration (a) can be calculated as:
Fnet=m⋅a
Rearranging gives:
a=Fnetm
a=58.8N60kg=0.98m/s2
The acceleration of the body is 0.98m/s2.
Similar Questions
A body of mass 60 kg is dragged with just enough force to start moving on a rough surface with coefficient of static and kinetic frictions 0.5 and 0.4 respectively . On applying the same force , what is the acceleration ?
View SolutionA body of weight 64 N is pushed with just enough force to start it moving across a horizontal floor and the same force continues to act afterwards. If the coefficients of static and dynamic friction are 0.6 and 0.4 respectively, the acceleration of the body will be (Acceleration due to gravity = g)
View SolutionA 60 kg body is pushed with just enough force to start it moving across a floor and the same force continues to act afterwards. The coefficient of static friction and sliding friction are 0.5 and 0.4 respectively. The acceleration of the body is
View SolutionA body of mass 40kg resting on a rough horizontal surface is subjected to a force P which is just enough to start the motion of the body. If μs=0.5μk=0.4,g=10ms−2 an dthe force P is continuously applied on the body, then the accceleration of the body is.
View SolutionA body of mass 40kg resting on a rough horizontal surface is subjected to a force P which is just enough to start the motion of the body. If μs=0.5μk=0.4,g=10ms−2 an dthe force P is continuously applied on the body, then the accceleration of the body is.
View SolutionA 60kg is pushed horizontaly with just enough force to start it moving across a floor and the same force continues to act afterwards. The coefficient of static friction and sliding friction are 0.5and 0.4 respectively the accleration of the body is
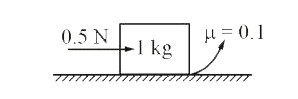
View SolutionA block of mass 1 kg in kept on a rough horizontal surface with μs=0.1 . A force of 0.5 N is applied as shown in the figure. What is the frictional force applied by ground on the block?
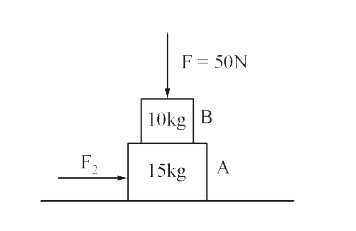
View SolutionBlock B is kept on Block A and a force F = 50 N pushes B down as shown in figure. Block A is kept on a rough surface with μs=0.2 and μk=0.1 . What is the maximum force F2 which can be applied so that the system remains at rest?
View SolutionA horizontal force just sufficient to move a body of mass 4kg lying on a rought horizontal surface is applied on it .The coefficient of static and kinetic friction the body and the surface are 0.8and0.6 respectively If the force contines to act even after the block has started moving the acceleration of the block in ms−2 is (g=10ms−2)
View SolutionA body of mass 5kg moves under a force of 10ˆi+10ˆj−20ˆk. What is the acceleration produced?
View Solution