Question

In the above problem, what force should the man exert on the rope to get his correct weight on the machine?

Explanation

To solve the problem of what force the man should exert on the rope to get his correct weight on the machine, we need to analyze the forces acting on him.

1. Understanding the Situation:
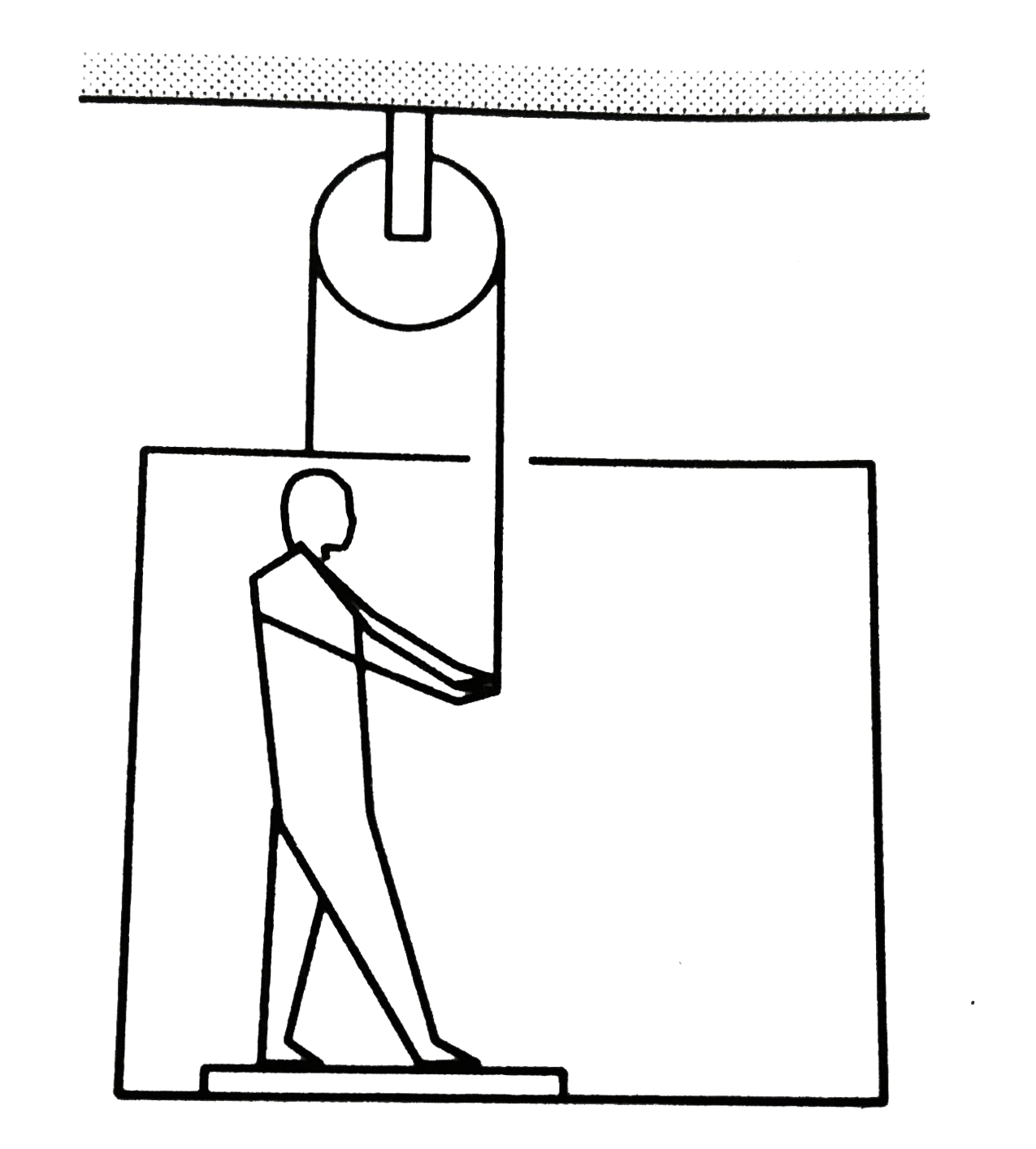
The man is standing on a weighing machine, and he is pulling on a rope. When he pulls the rope, he exerts a force that affects the reading on the weighing machine.

2. Identify Forces:
The forces acting on the man include:
- His weight (W = mg, where m is his mass and g is the acceleration due to gravity).
- The upward force exerted by the weighing machine (N).
- The force exerted by the man on the rope (F).

3. Applying Newton's Second Law:
When the man pulls on the rope, he creates a tension (T) in the rope. According to Newton's second law, the net force acting on him can be expressed as:
\( N - W + F = 0 \)
Rearranging gives:
\( N = W - F \)

4. Correct Weight on the Machine:
To read his correct weight on the machine, the normal force (N) should equal his actual weight (W). Therefore, we set:
\( N = W \)
Substituting this into the previous equation gives:
\( W = W - F \)

5. Solving for the Force (F):
Rearranging the equation:
\( F = 0 \)
This means that to get his correct weight on the machine, the man should not exert any force on the rope.

Conclusion:
The man should exert a force of 0 N on the rope to get his correct weight on the machine.