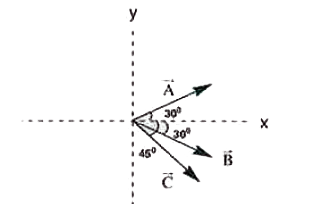
Three vectors →A,→B,→C are shown in the figure. Find angle between (i) →A and →B (ii) →B and →C , (iii) →A and →C
To find the angle between two vectors we connect the tails of the two vectors. We can shift the vectors parallel to themselves such that tails of A, B and are connected as shown in figure.
Now we observe that angle between →Aand→B is 60∘ B and C is 15∘ and between →Aand→C is 75∘
Topper's Solved these Questions
- MOTION IN A PLANEBOOK - AAKASH SERIESCHAPTER - MOTION IN A PLANEEXERCISE - EXERCISE-A (Vectors & Scalars)
25 Videos
- MOTION IN A PLANEBOOK - AAKASH SERIESCHAPTER - MOTION IN A PLANEEXERCISE - EXERCISE-A (Addition & Subtractions of Vectors)
10 Videos
- MAGNETISMBOOK - AAKASH SERIESCHAPTER - MAGNETISMEXERCISE - ADDITIONAL EXERCISE
22 Videos
- MOTION IN A PLANEBOOK - AAKASH SERIESCHAPTER - MOTION IN A PLANEEXERCISE - QUESTION FOR DESCRIPTIVE ANSWER
7 Videos
Similar Questions
Three vectors →A,→B,→C are shown in the figure angle between (i) →Aand→B(ii)→Band→C,(iii)→Aand→C

View SolutionIf →A,→B,→C represents the three sides of an equilateral triangle taken in the same order then find the angle between (i) →Aand→B(ii)→Band→C(iii)Aand→C.
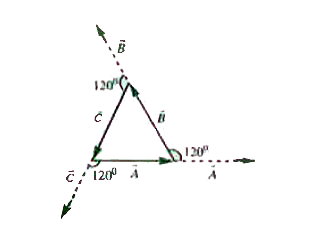
View SolutionIf →a+→b+→c=0,|→a|=3,∣∣→b∣∣=5,|→c|=7 , then find the angle between →aand→b.
View SolutionIf →a+→b+→c=0,|→a|=3,∣∣→b∣∣=5,|→c|=7 , then find the angle between →aand→b.
View SolutionIf →a+→b+→c=0,|→a|=3,∣∣→b∣∣=5,|→c|=7 , then find the angle between →aand→b.
View SolutionIf |→a|+∣∣→b∣∣=|→c|and→a+→b=→c then find the angle between →aand→b.
View SolutionLet →a,→b,→c be three unit vectors such that angle between →aand→bisα,→band→c is βand→cand→a is γ. if ∣∣→a.+→b+→c∣∣=2 , then cosα+cosβ+cosγ =
View SolutionIf →a+→b+→c=→0,|→a|=3,∣∣→b∣∣=5and|→c|=7 , then the angle between →aand→b is
View SolutionIf three unit vectors →a,→band→c satisfy→a+→b+→c=→0. Then find the angle between →aand→b.
View Solution→a+→b+→c=→0,|→a|=3,∣∣→b∣∣=5,|→c|=9,find the angle between →a and →c.
View Solution
