A swimmer is capable of swimming at 1.65ms- in still water. If he swims directly across a 180m wide river with water flow at 0.85ms−1', how far down stream will he reach? How long will it take to reach the other side ?
To solve the problem step by step, we will break down the components of the swimmer's movement across the river and calculate the required values.
Step 1: Identify the given values
- Speed of the swimmer in still water, Vs=1.65m/s
- Width of the river, d=180m
- Speed of the river current, Vr=0.85m/s
Step 2: Calculate the time taken to swim across the river
The time taken to swim across the river can be calculated using the formula:
Time=DistanceSpeed
Here, the distance is the width of the river, and the speed is the swimmer's speed in the vertical direction (across the river).
Time=dVs=180m1.65m/s≈109.09s
Step 3: Calculate how far downstream the swimmer will be carried
The distance the swimmer is carried downstream can be calculated using the formula:
Distance=Speed×Time
Here, the speed is the speed of the river current, and the time is the time taken to swim across the river.
Distance=Vr×Time=0.85m/s×109.09s≈92.73m
Summary of Results
- The time taken to reach the other side of the river is approximately 109.09s.
- The distance downstream the swimmer will reach is approximately 92.73m.
- Speed of the swimmer in still water, Vs=1.65m/s
- Width of the river, d=180m
- Speed of the river current, Vr=0.85m/s
The time taken to swim across the river can be calculated using the formula:
Time=DistanceSpeed
Here, the distance is the width of the river, and the speed is the swimmer's speed in the vertical direction (across the river).
The distance the swimmer is carried downstream can be calculated using the formula:
Distance=Speed×Time
Here, the speed is the speed of the river current, and the time is the time taken to swim across the river.
- The time taken to reach the other side of the river is approximately 109.09s.
- The distance downstream the swimmer will reach is approximately 92.73m.
Topper's Solved these Questions
- ELEMENTS OF VECTORSBook:AAKASH SERIESChapter:ELEMENTS OF VECTORSExercise:QUESTIONS FOR DESCRIPTIVE ANSWERS
Explore 10 Videos
- ELEMENTS OF VECTORSBook:AAKASH SERIESChapter:ELEMENTS OF VECTORSExercise:NUMERICAL EXXERCISE (LEVEL -1)
Explore 13 Videos
- ELECTROSTATICSBook:AAKASH SERIESChapter:ELECTROSTATICSExercise:ADDITIONAL PRACTICE EXERCISE (PRACTICE SHEET (ADVANCED) INTEGER TYPE QUESTIONS)
Explore 5 Videos
- GEOMETRICAL OPTICSBook:AAKASH SERIESChapter:GEOMETRICAL OPTICSExercise:ADDITIONAL PRACTICE EXERCISE (LEVEL-II PRACTICE SHEET (ADVANCED) INTEGER TYPE QUESTIONS)
Explore 10 Videos
Similar Questions
A man can swim at a speed of 3 km/h in still water. He wants t cross a 500 m wide river flowing at 2 km/h. He flow at an angle of 120 with the river flow while swimming. A. Find the time he takes to cross the river. b.At what point on the opposite bank will he arrive?
View SolutionA man can swim at a speed of 3kmh−1 in still water. He wants to cross a 500−m wide river flowing at 2kmh−1. He keeps himself always at an angle to 120∘ with the river flow while swimming.
The time taken to cross the river is.
View SolutionA river is following from west to east at a speed of 5m/minute. A boy on the south bank of the river, capable of swimming at 10 meters/minute in still water, wants to swin across the river in the shortest time, (i) Find the direction in which he should swin, (ii) find the direction when drift along the river is zero.
View SolutionA man can swim with a speed of 4kmh−1 in still water. He crosses a river 1km wide that flows steadly at 3kmh−1. If he makes his strokes normal to the river current, how far down the river does he go when he reaches the other bank?
View SolutionA man can swin with speed 6 km/h in still water. If he tries of swim across a river flowing with speed 5km/h, how fast does a leaf floating on water appears to go , to the man ?
View SolutionA man can swim at a speed of 3kmh−1 in still water. He wants to cross a 500−m wide river flowing at 2kmh−1. He keeps himself always at an angle to 120∘ with the river flow while swimming.
The drift of the man along the direction of flow, when he arrives at the opposite bank is.
View SolutionBoat moves with velocity 5 m/s on still water. It is steered perpendicular to the river current.
(a) Will it reach point B or somewhere else on the other bank ?
(b) How long will it take to cross the river?
(c) How far down stream, will it reach the other bank ?
(d) Does it take minimum time in this way ?
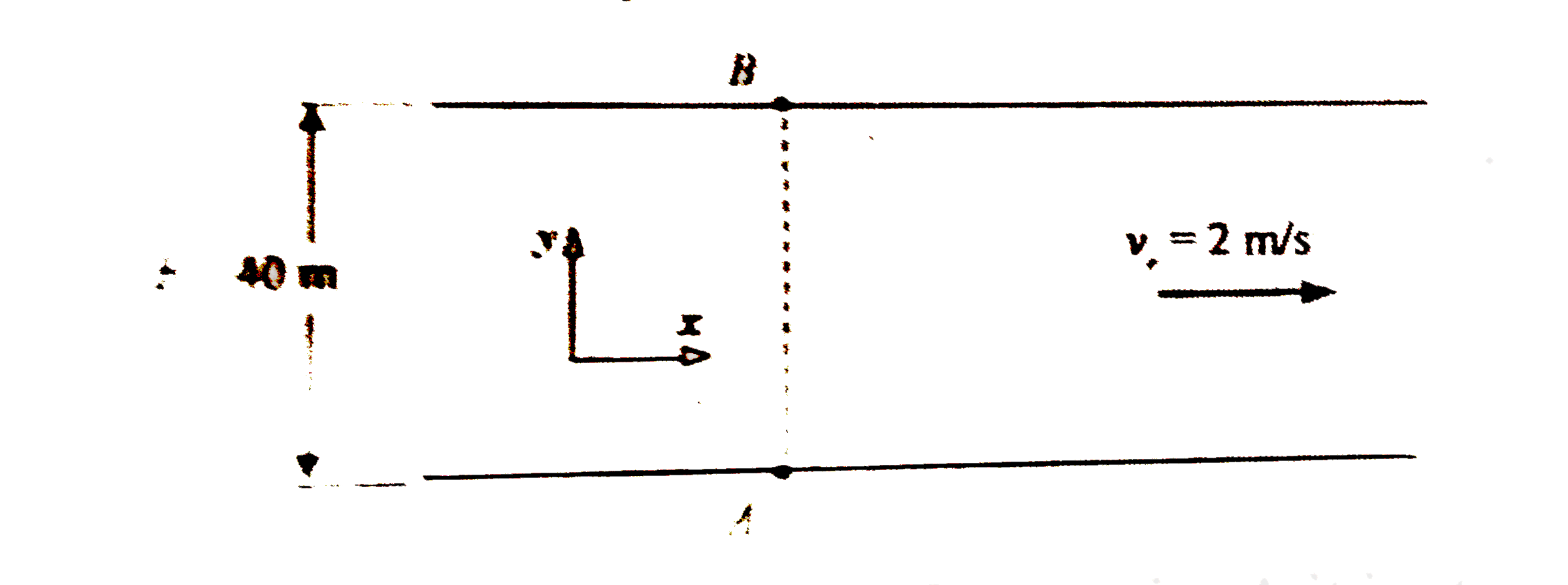
View SolutionA swimmer can swim in still water with a speed of 3 ms−1 While crossing a river his average speed is 5 ms−1 If crosses the river in the shortest possible time, what is the speed of flow of water ?
View SolutionA man can swim in still water with a speed of 2ms−1. If he wants to cross a river of water current speed √3ms−1 along the shortest possible path, then in which direction should he swim ?
View SolutionA swimmer capable of swimming with velocity v relative to water jumps in a flowing river having velocity u. The man swims a distance d down stream and returns back to the original position. Find out the time taken in complete motion.
View Solution

