vector is not changed if
it is rotated through an arbitrary angle
it is multiplied by an arbitrary scalar
it is cross multiplied by a unit vector
it is slid parallel to itself.
The correct Answer is:D
To determine when a vector does not change, we need to analyze each option provided in the question.
1. Understanding Vector Properties:
A vector is defined by both its magnitude and direction. For a vector to remain unchanged, both these properties must stay the same.
2. Evaluating Option 1:
- Statement: A vector is not changed if it is rotated through an arbitrary angle.
- Analysis: Rotating a vector changes its direction. Since the direction of the vector changes, the vector itself is altered.
- Conclusion: This option is incorrect.
3. Evaluating Option 2:
- Statement: A vector is not changed if it is multiplied by an arbitrary scalar.
- Analysis: Multiplying a vector by a scalar changes its magnitude. Therefore, the vector is not the same after this operation.
- Conclusion: This option is incorrect.
4. Evaluating Option 3:
- Statement: A vector is not changed if it is cross-multiplied by a unit vector.
- Analysis: Cross-multiplying a vector with a unit vector results in a new vector that is perpendicular to both. This operation changes the direction and magnitude of the original vector.
- Conclusion: This option is incorrect.
5. Evaluating Option 4:
- Statement: A vector is not changed if it is slid parallel to itself.
- Analysis: Sliding a vector parallel to itself means that both its magnitude and direction remain unchanged. The vector retains its original properties.
- Conclusion: This option is correct.
Final Answer:
The vector is not changed if it is slid parallel to itself.
---
A vector is defined by both its magnitude and direction. For a vector to remain unchanged, both these properties must stay the same.
- Statement: A vector is not changed if it is rotated through an arbitrary angle.
- Analysis: Rotating a vector changes its direction. Since the direction of the vector changes, the vector itself is altered.
- Conclusion: This option is incorrect.
- Statement: A vector is not changed if it is multiplied by an arbitrary scalar.
- Analysis: Multiplying a vector by a scalar changes its magnitude. Therefore, the vector is not the same after this operation.
- Conclusion: This option is incorrect.
- Statement: A vector is not changed if it is cross-multiplied by a unit vector.
- Analysis: Cross-multiplying a vector with a unit vector results in a new vector that is perpendicular to both. This operation changes the direction and magnitude of the original vector.
- Conclusion: This option is incorrect.
- Statement: A vector is not changed if it is slid parallel to itself.
- Analysis: Sliding a vector parallel to itself means that both its magnitude and direction remain unchanged. The vector retains its original properties.
- Conclusion: This option is correct.
The vector is not changed if it is slid parallel to itself.
Similar Questions
(A): The direction of velocity vector remains unchanged though the coordinate system is changed
(R) : The direction of real vector is independent of coordinate system
View SolutionAsserion: Magnitude of the resultant of two vectors may be less than the magnitude of either vector.
Reason: The resultant of two vectors is obtained by means of law of parallelogram of Vectors.
View Solution
Knowledge Check
An impulse is supplied to a moving object with the force at an angle of 120∘ with respect to velocity vector. The angle between the impulse vector and the change in momentum vector is
A120∘B0∘C60∘D240∘
Assertion : Acceleration of a moving particle can change its direction without any change in direction of velocity.
Reason : If the direction of change in velocity vector changes, the direction of acceleration vector also changes.
View SolutionAssertion : Acceleration of a moving particle can change its direction without any change in direction of velocity.
Reason : If the direction of change in velocity vector changes, the direction of acceleration vector also changes.
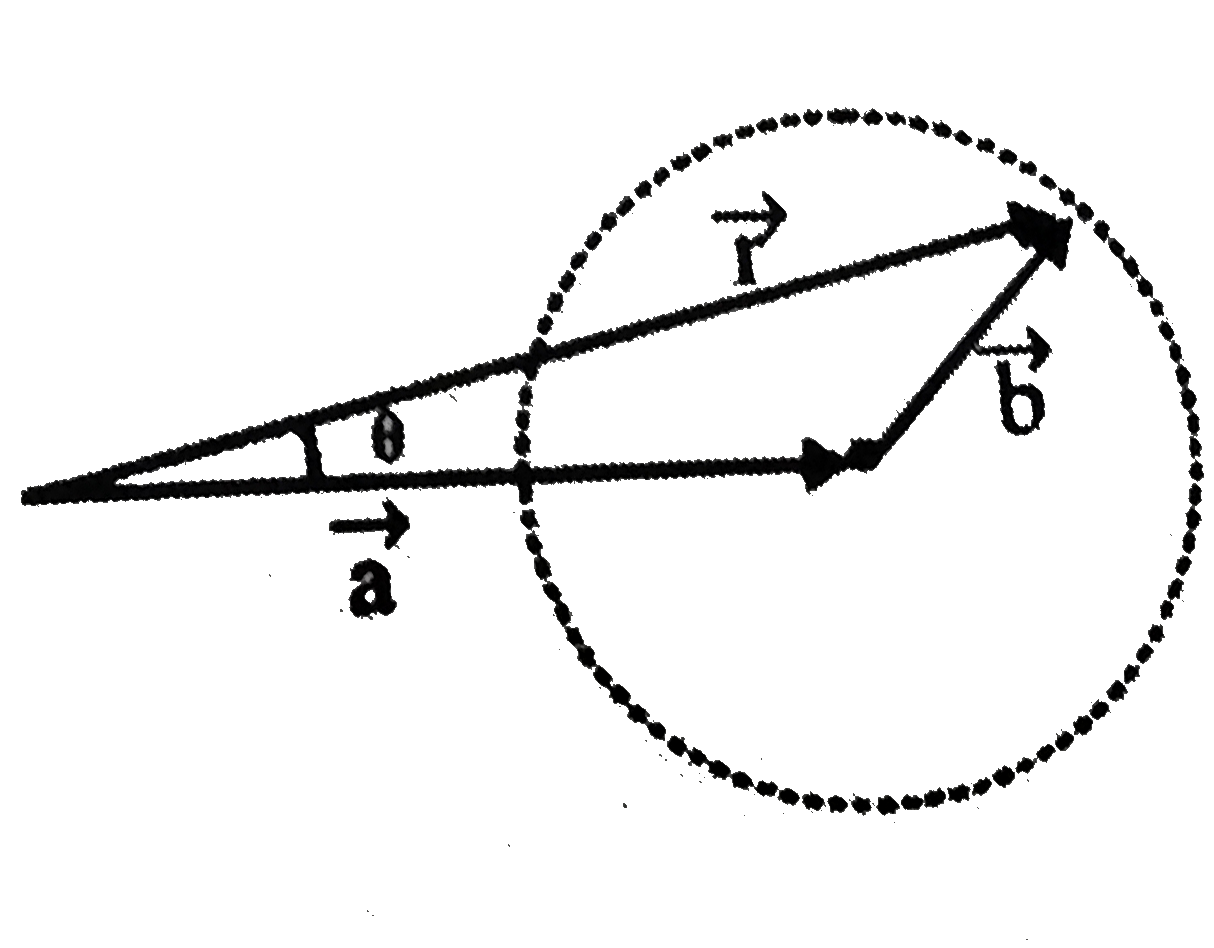
View SolutionKeeping one vector constant, if direction of other to be added in the first vector is changed continuously, tip of the resultant vector describes a circles, In the following figure vector →a is kept constant. When vector →b addede to →a changes its direction, the tip of the resultant vector →r=→a+→b describes circles of radius b with its centre at the tip of vector →a. Maximum angle between vector →a and the resultant →r=→a+→b is
View SolutionThe result of scalar product and the vector product of two given vectors is zero . If one vector is ˆi what is the other vector ?
View SolutionResultant of two vectors one having magnitude twice of other is perpendicular to the smaller vector then find the angle ( in∘) between the vectors ?
View SolutionA vector may change when we :
View SolutionA vector may change when we :
View Solution

