What is the displacement of the point of a wheel initially in contact with the ground when the wheel rolls forward half a revolution ? Take the radius of the wheel as R and the the x - axis as the forward direction ?
To find the displacement of the point of a wheel that is initially in contact with the ground after rolling forward half a revolution, we can follow these steps:
1. Understand the Problem:
- We have a wheel of radius R.
- The wheel rolls forward half a revolution.
- We need to find the displacement of the point that was initially in contact with the ground.
2. Determine the Distance Traveled:
- The circumference of the wheel is given by 2πR.
- For half a revolution, the distance traveled by the wheel in the horizontal direction is:
Distance=12×2πR=πR
3. Identify the Initial and Final Positions:
- Let the initial position of the point in contact with the ground be point A.
- After rolling half a revolution, this point will move to the topmost position of the wheel, which we can call point B.
4. Draw a Right Triangle:
- The horizontal distance traveled (from point A to the vertical line below point B) is πR.
- The vertical distance (from point A to point B) is equal to the diameter of the wheel, which is 2R.
5. Apply the Pythagorean Theorem:
- To find the displacement AC (where C is the final position of the point after half a revolution), we can use the Pythagorean theorem:
AC=√(AB)2+(BC)2
- Here, AB=πR and BC=2R.
- Therefore:
AC=√(πR)2+(2R)2=√π2R2+4R2=√R2(π2+4)=R√π2+4
6. Final Result:
- The displacement of the point initially in contact with the ground after rolling half a revolution is:
Displacement=R√π2+4
- We have a wheel of radius R.
- The wheel rolls forward half a revolution.
- We need to find the displacement of the point that was initially in contact with the ground.
- The circumference of the wheel is given by 2πR.
- For half a revolution, the distance traveled by the wheel in the horizontal direction is:
Distance=12×2πR=πR
- Let the initial position of the point in contact with the ground be point A.
- After rolling half a revolution, this point will move to the topmost position of the wheel, which we can call point B.
- The horizontal distance traveled (from point A to the vertical line below point B) is πR.
- The vertical distance (from point A to point B) is equal to the diameter of the wheel, which is 2R.
- To find the displacement AC (where C is the final position of the point after half a revolution), we can use the Pythagorean theorem:
AC=√(AB)2+(BC)2
- Here, AB=πR and BC=2R.
- Therefore:
AC=√(πR)2+(2R)2=√π2R2+4R2=√R2(π2+4)=R√π2+4
- The displacement of the point initially in contact with the ground after rolling half a revolution is:
Displacement=R√π2+4
Topper's Solved these Questions
- MOTION IN A PLANEBook:AAKASH SERIESChapter:MOTION IN A PLANEExercise:SHORT ANSWER TYPE QUESTIONS
Explore 6 Videos
- MOTION IN A PLANEBook:AAKASH SERIESChapter:MOTION IN A PLANEExercise:VERY SHORT ANSWER TYPE QUESTIONS
Explore 10 Videos
- MOTION IN A PLANEBook:AAKASH SERIESChapter:MOTION IN A PLANEExercise:EXERCISE-3 (Circular Motion)
Explore 7 Videos
- MOTION IN A STRAIGHT LINE Book:AAKASH SERIESChapter:MOTION IN A STRAIGHT LINE Exercise:very Short answer type question
Explore 15 Videos
Similar Questions
A Wheel of circumference C is at rest on the ground.When the wheel rolls forward through half a revolution ,then the displacement of point contact will be
View SolutionA wheel of perimeter 4π is rolling on a horizontal surface. The displacement of the point of contact of wheel and ground when the wheel completes one quarter of revolution is
View SolutionA wheel is released on a rough horizontal floor after imparting it an initial horizontal velocity v0 and angular velocityω0 as shown in the figure below. Point O is the centre of mass of the wheel and point P is its instantaneous point of contact with the groundl. The radius of wheel is r and its radius of gyration about O is k. Coefficient of friction between wheel and ground is μ. A is a fixed point on the ground.
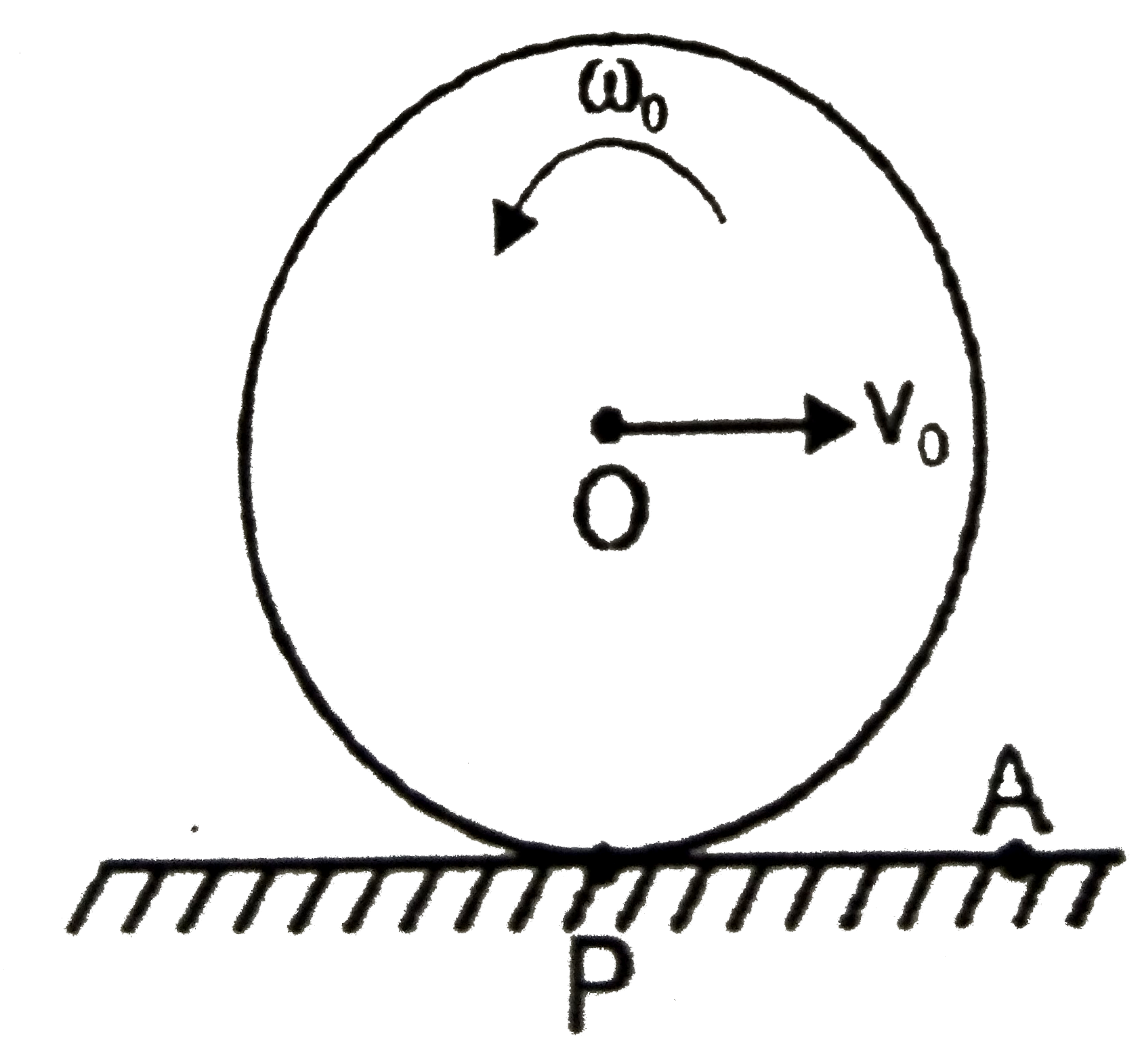
If the wheel comes to permanent rest after sometimes, then :
View SolutionA wheel is released on a rough horizontal floor after imparting it an initial horizontal velocity v0 and angular velocityω0 as shown in the figure below. Point O is the centre of mass of the wheel and point P is its instantaneous point of contact with the groundl. The radius of wheel is r and its radius of gyration about O is k. Coefficient of friction between wheel and ground is μ. A is a fixed point on the ground.
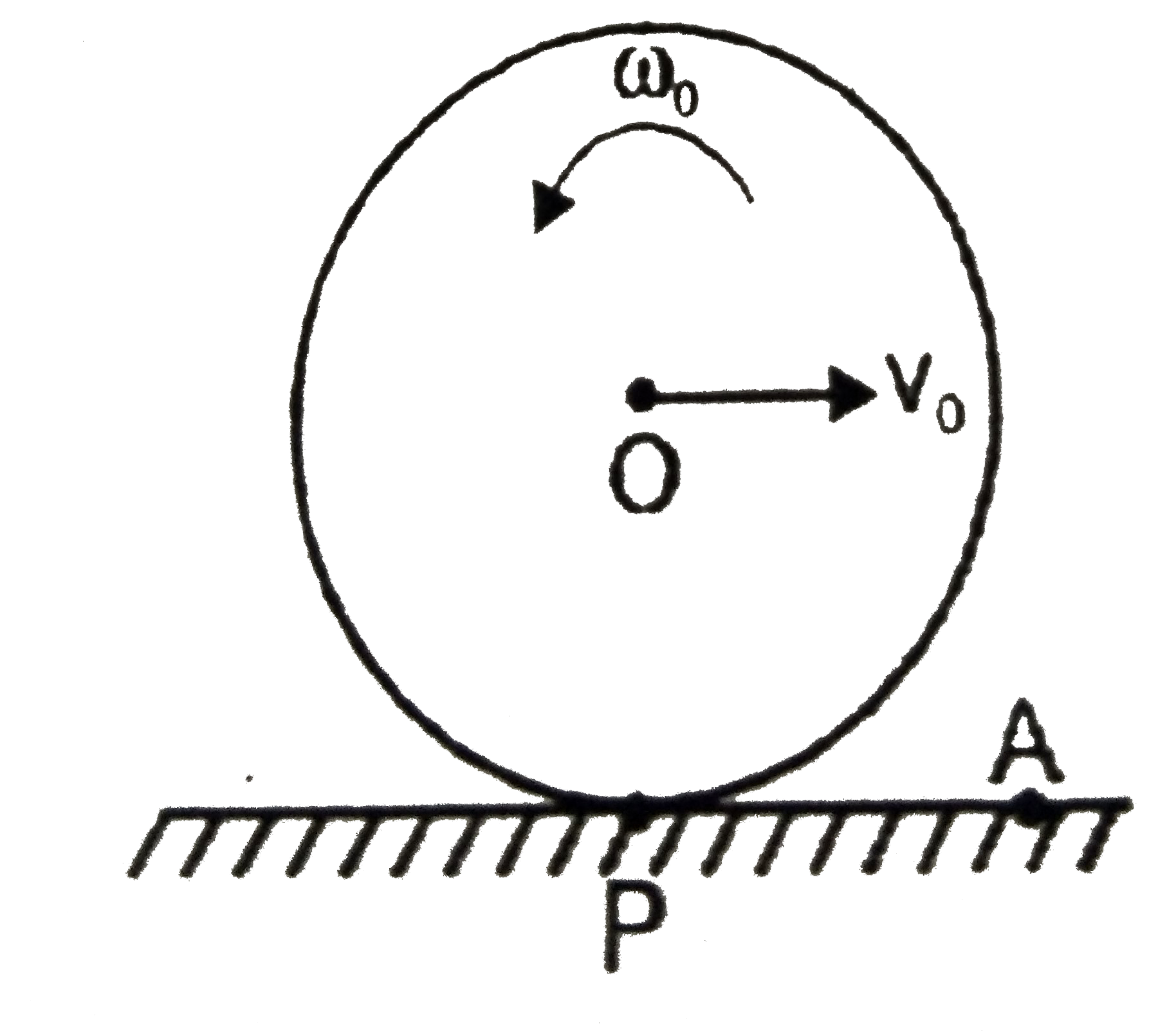
If above question , distance travelled by centre of mass of the wheel before it stops is −
View SolutionA wheel is released on a rough horizontal floor after imparting it an initial horizontal velocity v0 and angular velocityω0 as shown in the figure below. Point O is the centre of mass of the wheel and point P is its instantaneous point of contact with the groundl. The radius of wheel is r and its radius of gyration about O is k. Coefficient of friction between wheel and ground is μ. A is a fixed point on the ground.
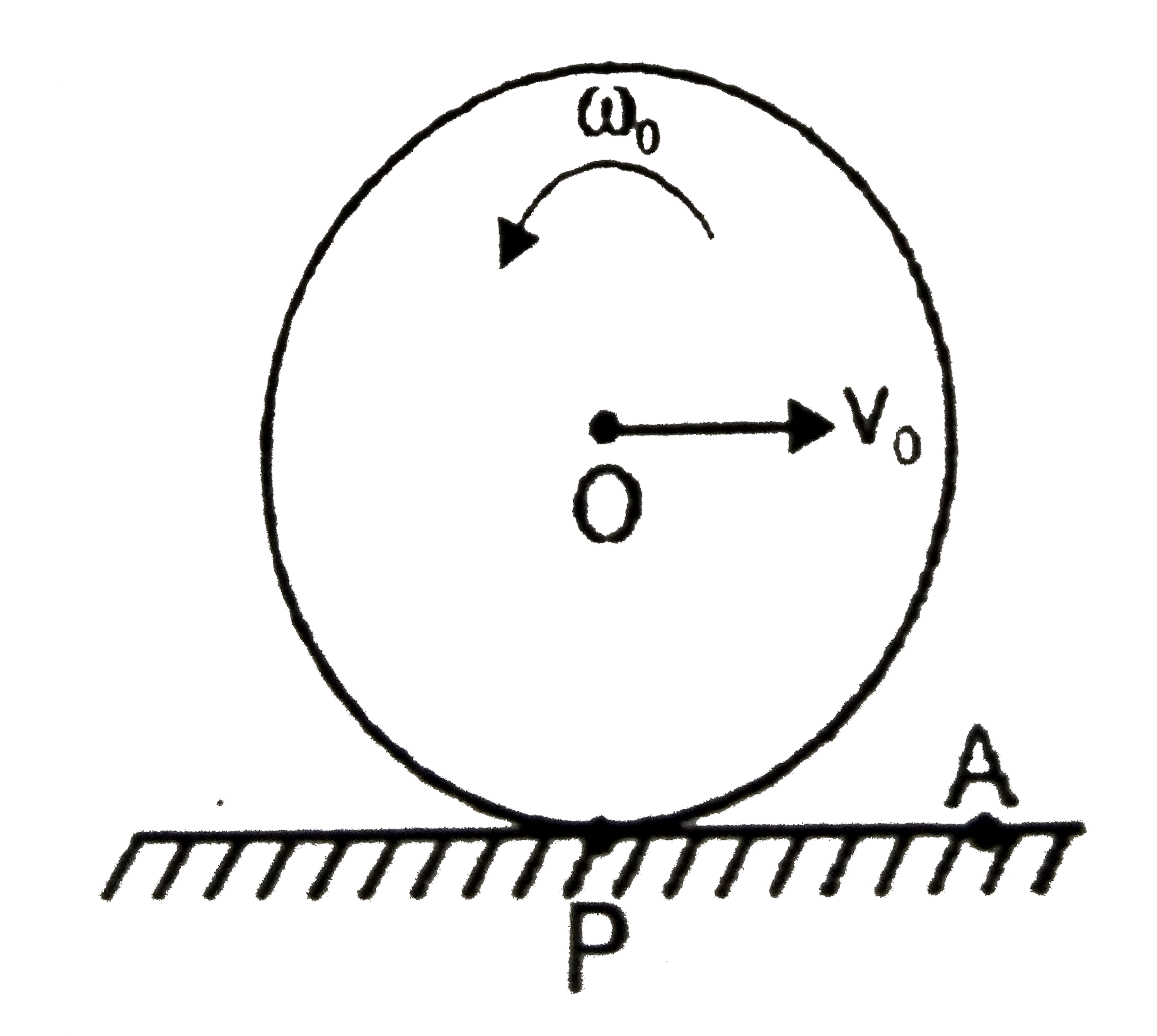
Which of the following is conserved ?
View SolutionA point P consider at contact point of a wheel on ground which rolls on ground without sliping then value of displacement of point P when wheel completes half of rotation (If radius of wheel is 1m) : -
View SolutionIf a given point P is in contact with ground initially and wheel of radius R is in pure rolling, then the displacement of point P when point P reaches topmost of the sphere for the first time will be

View SolutionThe radius of a wheel of a bus is 45 cm. Determine its speed in kilometres per hour, when its wheel makes 315 revolutions per minute
View SolutionA wheel of radius 1m rolls forward half a revolution on a horizontal ground. The magnitude of the displacement of the point of the wheel initially on contact with the ground is.
View Solution(A) : When a bicycle is in motion, the force of friction exerted by the ground on the two wheels is always in forward direction.
(R ) : The frictional force only when the bodies are in contact.
View Solution

