A copper block of mass 'm' at temperature is kept in the open atmosphere at temperature where . The variation of entropy of the copper block with time is best illustrated by




The correct Answer is:C
To solve the problem of how the entropy of a copper block changes over time when it is placed in an environment with a higher temperature, we can follow these steps:
1. Understanding the Initial Conditions:
- We have a copper block with mass 'm' at an initial temperature T1.
- The block is placed in an open atmosphere at a higher temperature T2 (where T2>T1).
- The initial entropy of the copper block at time t=0 is denoted as S0.
Hint: Remember that entropy is a measure of disorder or randomness in a system, and it is affected by temperature changes.
2. Heat Transfer:
- Since T2>T1, heat will flow from the surroundings (at temperature T2) into the copper block (at temperature T1).
- This heat transfer will cause the temperature of the copper block to increase over time.
Hint: Consider the direction of heat flow and how it affects the temperature of the block.
3. Change in Entropy:
- As the copper block absorbs heat, its entropy will increase. The relationship between heat transfer and entropy change is given by:
ΔS=QT
- Here, Q is the heat absorbed by the copper block, and T is the temperature at which the heat transfer occurs. As the temperature of the block increases, the entropy change will also increase.
Hint: Think about how entropy changes with temperature and how it is related to heat transfer.
4. Equilibrium Condition:
- The process continues until the temperature of the copper block equals the temperature of the surroundings (T1=T2). At this point, the system reaches thermal equilibrium.
- At equilibrium, there is no further heat transfer, and thus the entropy of the copper block will remain constant.
Hint: Identify the point at which the system reaches equilibrium and how that affects the entropy.
5. Graphical Representation:
- The graph of entropy (y-axis) versus time (x-axis) will start at a finite value S0 and will increase continuously as the block absorbs heat until it reaches equilibrium.
- After reaching equilibrium, the entropy will remain constant, indicating no further change.
Hint: Visualize how the graph would look based on the behavior of the system over time.
Conclusion:
The correct illustration of the variation of entropy of the copper block with time would show an initial increase in entropy that continues until the block reaches thermal equilibrium with the surrounding atmosphere, after which the entropy remains constant.
Final Answer:
The correct option is C, which illustrates the increase in entropy over time until equilibrium is reached.
- We have a copper block with mass 'm' at an initial temperature T1.
- The block is placed in an open atmosphere at a higher temperature T2 (where T2>T1).
- The initial entropy of the copper block at time t=0 is denoted as S0.
- Since T2>T1, heat will flow from the surroundings (at temperature T2) into the copper block (at temperature T1).
- This heat transfer will cause the temperature of the copper block to increase over time.
- As the copper block absorbs heat, its entropy will increase. The relationship between heat transfer and entropy change is given by:
ΔS=QT
- Here, Q is the heat absorbed by the copper block, and T is the temperature at which the heat transfer occurs. As the temperature of the block increases, the entropy change will also increase.
- The process continues until the temperature of the copper block equals the temperature of the surroundings (T1=T2). At this point, the system reaches thermal equilibrium.
- At equilibrium, there is no further heat transfer, and thus the entropy of the copper block will remain constant.
- The graph of entropy (y-axis) versus time (x-axis) will start at a finite value S0 and will increase continuously as the block absorbs heat until it reaches equilibrium.
- After reaching equilibrium, the entropy will remain constant, indicating no further change.
The correct illustration of the variation of entropy of the copper block with time would show an initial increase in entropy that continues until the block reaches thermal equilibrium with the surrounding atmosphere, after which the entropy remains constant.
The correct option is C, which illustrates the increase in entropy over time until equilibrium is reached.
Similar Questions
A solid at temperature T1 is kept in an evacuated chamber at temperature T2>T1 . The rate of increase of temperature of the body is propertional to
View SolutionIf K1 is the equilibrium constant at temperature T1andK2 is the equilibrium constant at temperature T2and If T2>T1 and reaction is endothermic then
View Solution
Knowledge Check
Two bars of same length and same cross-sectional area but of different thermal conductivites K1 and K2 are joined end to end as shown in the figure. One end of the compound bar it is at temperature T1 and the opposite end at temperature T2 (whereT1>T2). The temperature of the junction is
 AK1T1+K2T2K1+K2BK1T2+K2T1K1+K2CK1(T1+T2)K1+K2DK2T1+T2K1
AK1T1+K2T2K1+K2BK1T2+K2T1K1+K2CK1(T1+T2)K1+K2DK2T1+T2K1Assertion : Current versus potential difference (i-V) graph for a conductor at two different temperatures T1 and T2 is shown in figure. Hence T1>T2.
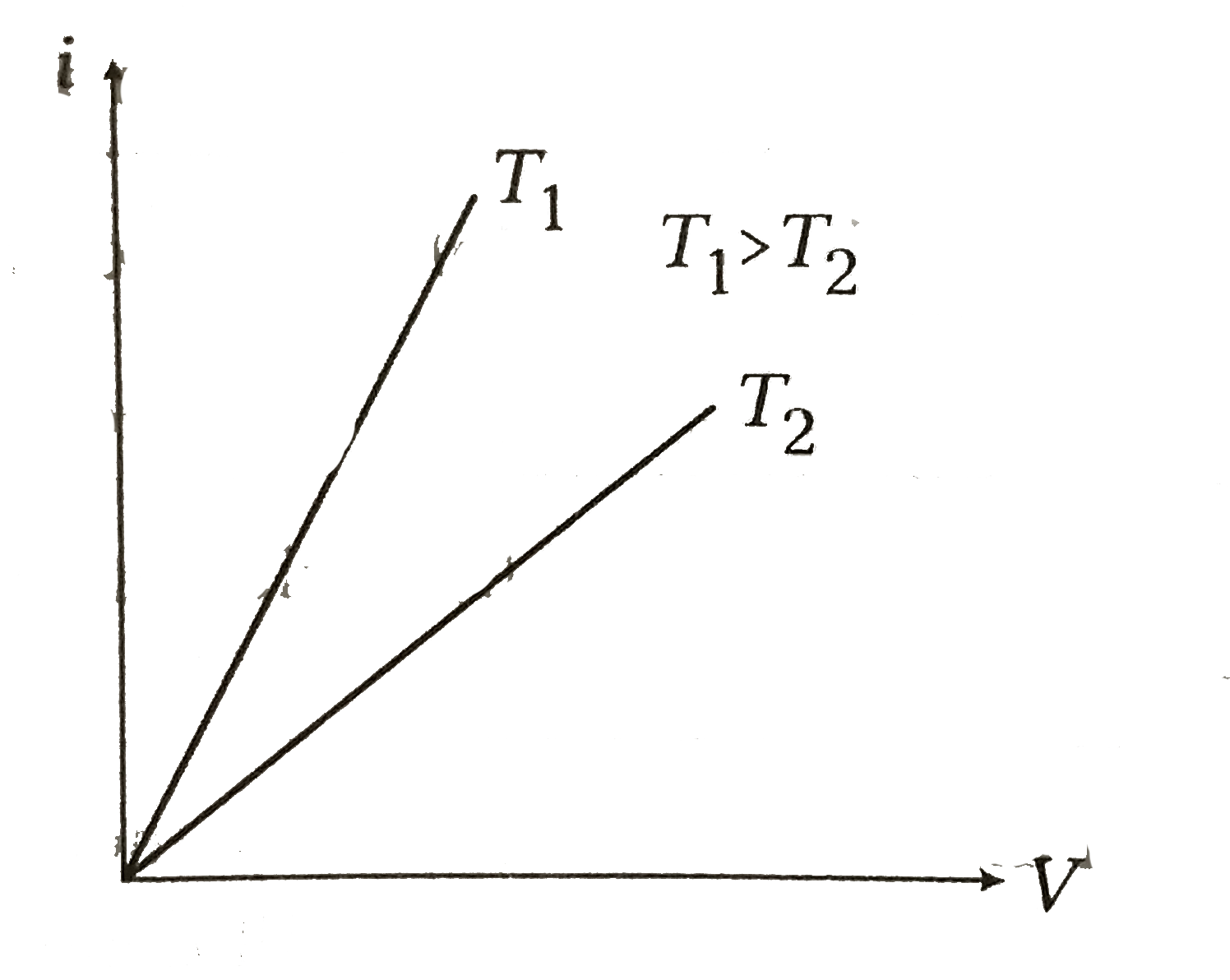
Reason : Resistance of a conductor increases with rise in temperature.Acos2θBsin2θCcot2θDtan2θThe isothermal diagram of a gas at three different temperatures T1,T2andT3, is show in the given figure .Then
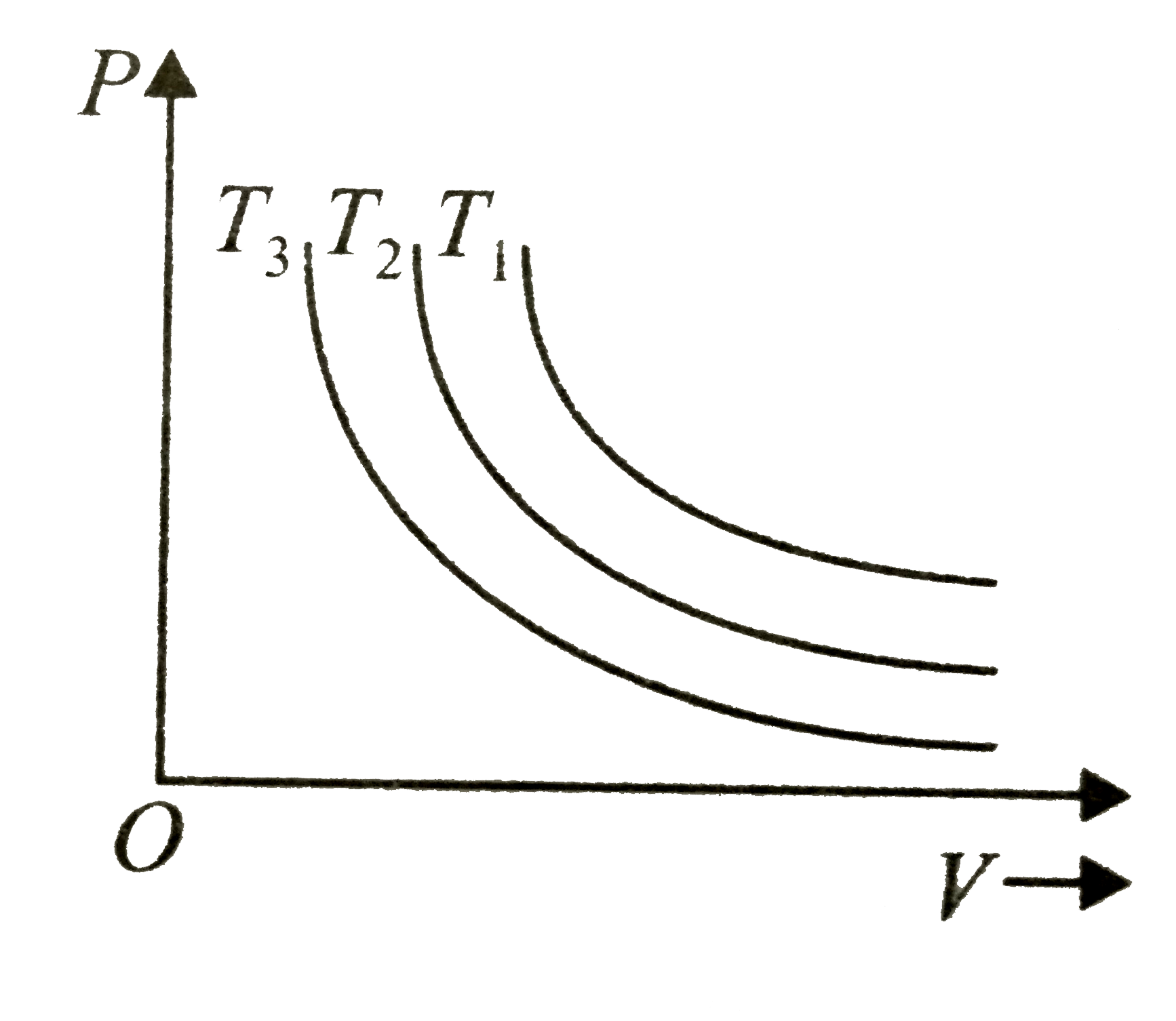 Aa.T1<T2<TBb. T1<T2>T3Cc.T1>T2>T3Dd.T1>T2<T3
Aa.T1<T2<TBb. T1<T2>T3Cc.T1>T2>T3Dd.T1>T2<T3
Shown below are the black body radiation curves at temperature T1 and T2(T2>T1). Which of the following plots is correct?
View SolutionOne end of a rod of length L and crosssectional area A is kept in a furnace at temperature T1. The other end of the rod is kept at a temperature T2. The thermal conductivity of the matrieal of the rod is K and emissivity of the rod is e. It is gives that T!=Ts+ΔT, where ΔT<<Ts,Ts is the temperature of the surroundings. If ΔT∝(T1−T2) find the proportional constant, consider that heat is lost only by rediation at the end where the temperature of the rod is T1.

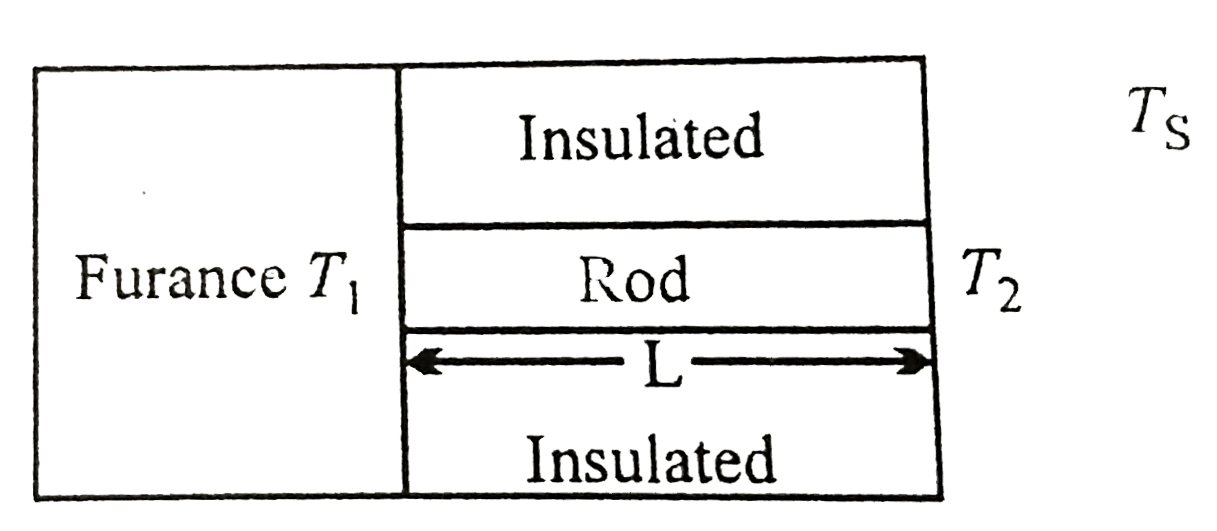
View SolutionOne end of rod of length L and cross-sectional area A is kept in a furance of temperature T1. The other end of the rod is kept at at temperature T2. The thermal conductivity of the material of the rod is K and emissivity of the rod is e. It is given that T2=TS+ΔT where ΔT<<TS, TS being the temperature of the surroundings. If ΔT∝(T1−TS), find the proportionality constant. Consider that heat is lost only by radiation at the end where the temperature of the rod is T2.
View SolutionA copper ball of mass 100 gm is at a temperature T. It is dropped in a copper calorimeter of mass 100 gm, filled with 170 gm of water at room temperature. Subsequently, the temperature of the system is found to be 75∘C . T is given by : (Given : room temperature = 30∘C, specific heat of copper =0.1cal/gm∘C)
View SolutionA rod of length l and cross-section area A has a variable thermal conductivity given by K = α T, where α is a positive constant and T is temperature in kelvin. Two ends of the rod are maintained at temperature T1 and T2 (T1>T2). Heat current flowing through the rod will be
View Solution

