What is the missing termin this A.P?2,25,________,71
38
43
36
48
To find the missing term in the arithmetic progression (A.P.) given as 2, 25, ____, 71, we can follow these steps:
Step 1: Identify the first term (a) and the last term.
The first term (a) is 2, and the last term (l) is 71.
Step 2: Determine the number of terms (n).
In this sequence, we have:
- First term (a) = 2
- Second term = 25
- Third term = ?
- Fourth term = 71
This means we have 4 terms in total (n = 4).
Step 3: Calculate the common difference (d).
The common difference (d) can be calculated using the first two terms:
d=Second term−First term=25−2=23
Step 4: Use the formula for the nth term of an A.P.
The formula for the nth term of an A.P. is given by:
an=a+(n−1)⋅d
Step 5: Find the missing term (the third term).
We need to find the third term (a3):
a3=a+(3−1)⋅d
a3=2+(2)⋅23
a3=2+46
a3=48
Conclusion:
The missing term in the A.P. is 48.
The first term (a) is 2, and the last term (l) is 71.
In this sequence, we have:
- First term (a) = 2
- Second term = 25
- Third term = ?
- Fourth term = 71
The common difference (d) can be calculated using the first two terms:
d=Second term−First term=25−2=23
The formula for the nth term of an A.P. is given by:
an=a+(n−1)⋅d
We need to find the third term (a3):
a3=a+(3−1)⋅d
a3=2+(2)⋅23
a3=2+46
a3=48
The missing term in the A.P. is 48.
Similar Questions
What is the missing label at
P,
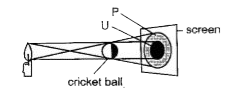
View SolutionWhat is the 99th term of the A.P. 2,2,2,…. ?
View SolutionIn the following A.P.'s, find the missing terms in the boxes.

View SolutionIn the following A.P.s , find the missing terms in the boxes :

View SolutionIn the following A.P.s , find the missing terms in the boxes :
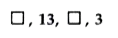
View SolutionIn the following A.P.s , find the missing terms in the boxes :
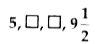
View SolutionIn the following A.P.s , find the missing terms in the boxes :
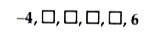
View SolutionIn the following A.P.s , find the missing terms in the boxes :
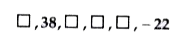
View SolutionIn the following A.P. 's find the missing terms in the boxes :
2,□,26
View SolutionIn the following A.P. 's find the missing terms in the boxes :
5,□,□,912
View Solution