A particle movinbg along a striaght line travels 100 m in 10 second and 200 m in the 20 second. Find the distance travelled by it in 30 seconds
240m
300 m
200 m
280 m
To solve the problem of finding the distance traveled by a particle in 30 seconds, we will analyze the information given in the question step by step.
Step 1: Understand the given data
The particle travels:
- 100 meters in the first 10 seconds
- 200 meters in the next 10 seconds (from 10 seconds to 20 seconds)
Step 2: Calculate the speed for each segment
1. For the first segment (0 to 10 seconds):
- Distance = 100 m
- Time = 10 s
- Speed = Distance / Time = 100 m / 10 s = 10 m/s
2. For the second segment (10 to 20 seconds):
- Distance = 200 m
- Time = 10 s (from 10 s to 20 s)
- Speed = Distance / Time = 200 m / 10 s = 20 m/s
Step 3: Determine the pattern of motion
From the calculations:
- The speed in the first segment (0 to 10 seconds) is 10 m/s.
- The speed in the second segment (10 to 20 seconds) is 20 m/s.
Step 4: Assume the speed for the next segment
To find the distance traveled in the next 10 seconds (from 20 to 30 seconds), we can assume that the particle continues to move at the speed of 20 m/s (the speed from the last segment).
Step 5: Calculate the distance for the next segment
- Time = 10 s (from 20 s to 30 s)
- Speed = 20 m/s
- Distance = Speed × Time = 20 m/s × 10 s = 200 m
Step 6: Calculate the total distance traveled in 30 seconds
Now, we add the distances traveled in each segment:
- Distance in the first 10 seconds = 100 m
- Distance in the next 10 seconds = 200 m
- Distance in the last 10 seconds = 200 m
Total distance = 100 m + 200 m + 200 m = 500 m
Final Answer
The distance traveled by the particle in 30 seconds is 500 meters.
---
The particle travels:
- 100 meters in the first 10 seconds
- 200 meters in the next 10 seconds (from 10 seconds to 20 seconds)
1. For the first segment (0 to 10 seconds):
- Distance = 100 m
- Time = 10 s
- Speed = Distance / Time = 100 m / 10 s = 10 m/s
- Distance = 200 m
- Time = 10 s (from 10 s to 20 s)
- Speed = Distance / Time = 200 m / 10 s = 20 m/s
From the calculations:
- The speed in the first segment (0 to 10 seconds) is 10 m/s.
- The speed in the second segment (10 to 20 seconds) is 20 m/s.
To find the distance traveled in the next 10 seconds (from 20 to 30 seconds), we can assume that the particle continues to move at the speed of 20 m/s (the speed from the last segment).
- Time = 10 s (from 20 s to 30 s)
- Speed = 20 m/s
- Distance = Speed × Time = 20 m/s × 10 s = 200 m
Now, we add the distances traveled in each segment:
- Distance in the first 10 seconds = 100 m
- Distance in the next 10 seconds = 200 m
- Distance in the last 10 seconds = 200 m
The distance traveled by the particle in 30 seconds is 500 meters.
Similar Questions
A body moving with uniform acceleration covers a distance of 14 m in first 2 second and 88 m in next 4 second. How much distance is travelled by it in 5th second?
View SolutionA body starting from test along straight line is traveling with an acceleration of 6ms−1, then the distance traveled by it in the 3rd seconds is ___________m
View Solution
Knowledge Check
The variation of velocity of a particle with time moving along a straight line is illustrated in the following figure. The distance travelled by the particle in four seconds is.
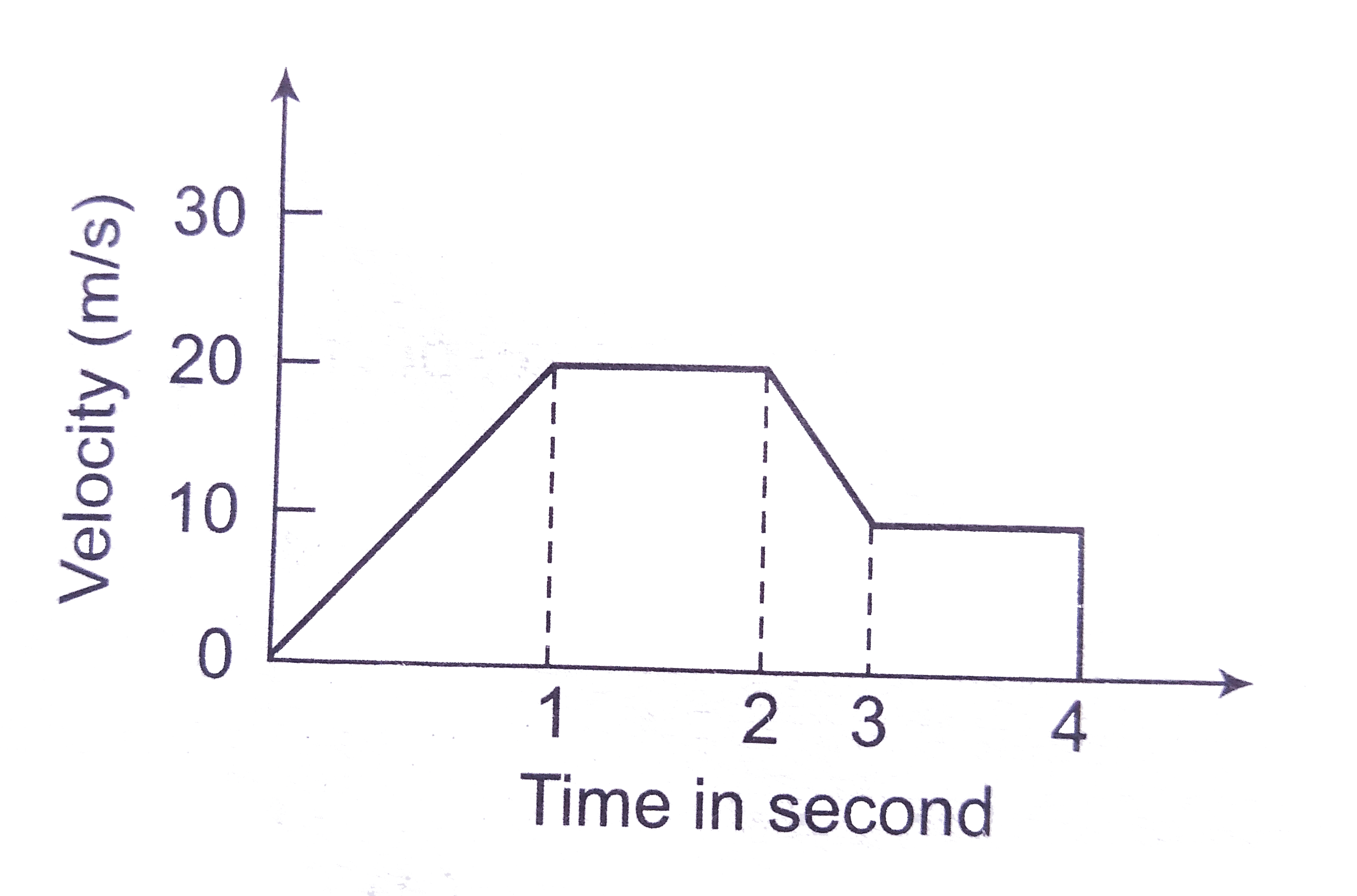 A60 mB55 mC25 mD30 m
A60 mB55 mC25 mD30 mA body starting from test along straight line is traveling with an acceleration of 6ms−1, then the distance traveled by it in the 3rd seconds is ___________m
A27B18C15D21
The variation of velocity of particle moving along a straight line is shown in the figure. The distance travelled by the particle in 4th second is
View SolutionThe variation of velocity of particle moving along a straight line is shown in the figure. The distance travelled by the particle in 4th second is?
View SolutionA particle travels a distance of 20 m in the 7th seconds and 24 m in 9th second. How much distance shall it travel in the 15th second?
View SolutionA particle having initial velocity 5m/s moves with a constant acceleration 2ms−2, for time 10 secondalong a straight line. Find the displacement of the particle in the last one second and the total distance traveled in 10 seconds.
View SolutionConsider a particle intially moving with a velocity of 5 m s−1 starts decelerating at a constant rate of 2 m s−2.
a. Determine the time at which the particle becomes stationary.
b. Find the distance travelled in the second second.
c. Find the distance travelled in the third second.
View SolutionA particle having initial velocity 4 m/s moves with a constant acceleration 1m/s2 for a time interval of 10 second in straight line. Find the displacement of the particle in the last second and the distance travelled in 10 second.
View Solution