Read the following text and answer the following questions on the basis of the same: The rate of increase in the number of bacteria in a certain bacteria culture is proportional to the number present. Given that the number triples in 5 hours.

If 'N' is the number of bacteria, the corresponding differential equation is ____________ .
dNdt=Kt
dNdt=KN
dKdt=N
dKdN=t
The correct Answer is:B
Step by step video, text & image solution for Read the following text and answer the following questions on the basis of the same: The rate of increase in the number of bacteria in a certain bacteria culture is proportional to the number present. Given that the number triples in 5 hours. If 'N' is the number of bacteria, the corresponding differential equation is ____________ . by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
Knowledge Check
∫1Kxdx=_________ .
Alog|x|+CBlog|Kx|+CC1Klog|x|+CD−1Kx2+CRead the following text and answer the following questions on the basis of the same: The rate of increase in the number of bacteria in a certain bacteria culture is proportional to the number present. Given that the number triples in 5 hours.

The general solution is _________ .Alog|N|=Kt+CBlog|Nt|=K+CClog|N|=tDlog|Kt|=N+CRead the following text and answer the following questions on the basis of the same: The rate of increase in the number of bacteria in a certain bacteria culture is proportional to the number present. Given that the number triples in 5 hours.

The bacteria becomes 10 times in ___________ hours.A5log7B5log10log3C5log3Dlog(1053)
Read of the following text and answer the following questions on the basis of the same:

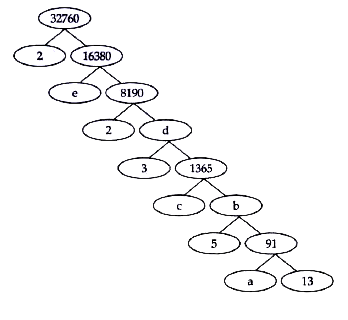
Find the value of e
View SolutionRead of the following text and answer the following questions on the basis of the same:
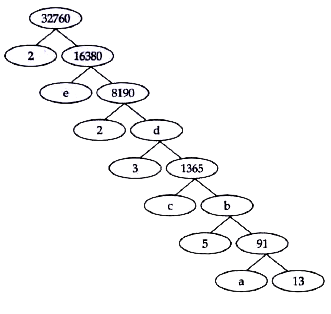
Find the value of b
View SolutionRead of the following text and answer the following questions on the basis of the same:
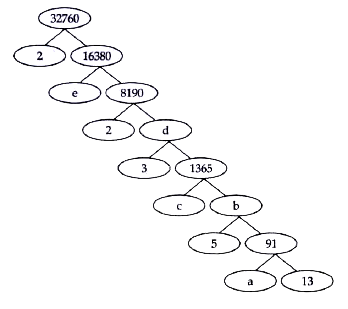
Find the value of d
View SolutionRead the following text and answer the following questions on the basis of the same:
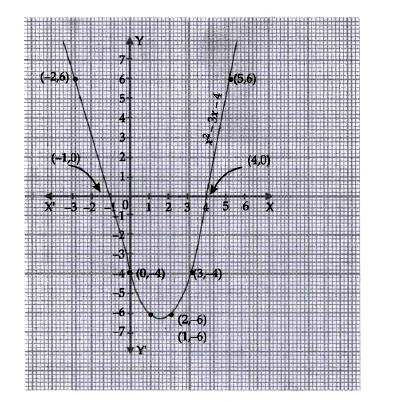
Name the shape of the graph
View SolutionRead the following text and answer the following questions on the basis of the same: The rate of increase in the number of bacteria in a certain bacteria culture is proportional to the number present. Given that the number triples in 5 hours.

If N0 is the initial count of bacteria, after 10 hours the count is __________ .
View Solution