Rashid is studying in class V. He can classify various types of triangles in different categories but has difficulty in understanding the abstract proof for the sum of three angles in a triangle to be always 180. According to Piaget Cognitive Theory, Rashid is at:

Concrete operational stage

Formal operational stage

Sensorimotor stage

Pre-operational stage

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

Updated on:21/07/2023

Answer

Step by step video, text & image solution for Rashid is studying in class V. He can classify various types of triangles in different categories but has difficulty in understanding the abstract proof for the sum of three angles in a triangle to be always 180. According to Piaget Cognitive Theory, Rashid is at: by Environmental Studies experts to help you in doubts & scoring excellent marks in Class 14 exams.

Updated on:21/07/2023

Class 14 ENVIRONMENTAL STUDIES EVS CONTENT AND PEDAGOGY

Knowledge Check

After the faliure of Bohr atomic theory but its ability to explain to the atomic spectral a need was felt for the new model that could incorporate, the concept of stationary orbit, de Broglie concept, Heisenberg uncertainity principle. The concept that in corporate above facts is called quantum mechanics of the atomic model wave mchanical model. it includes set of quantum number and $∣ ∣ ψ^{2} ∣ ∣$ a mathematical expression of the probability of finding an electron at all points in space. This probability function is the best indication available of how the electon behaves, for as a consequence of the Uncertainity Principle, the amount we can know about the electron is limited. While quantum mechanics can tell us the exact probability of finding an electron at any two particular points, it does not tell us how the electron moves from one of these points to the other. Thus the idea of an electron orbit is lost, it is replaced with a description of where the electron is most likely to be found. This total picture of the probability of finding an electron at various points in space is called an orbital.

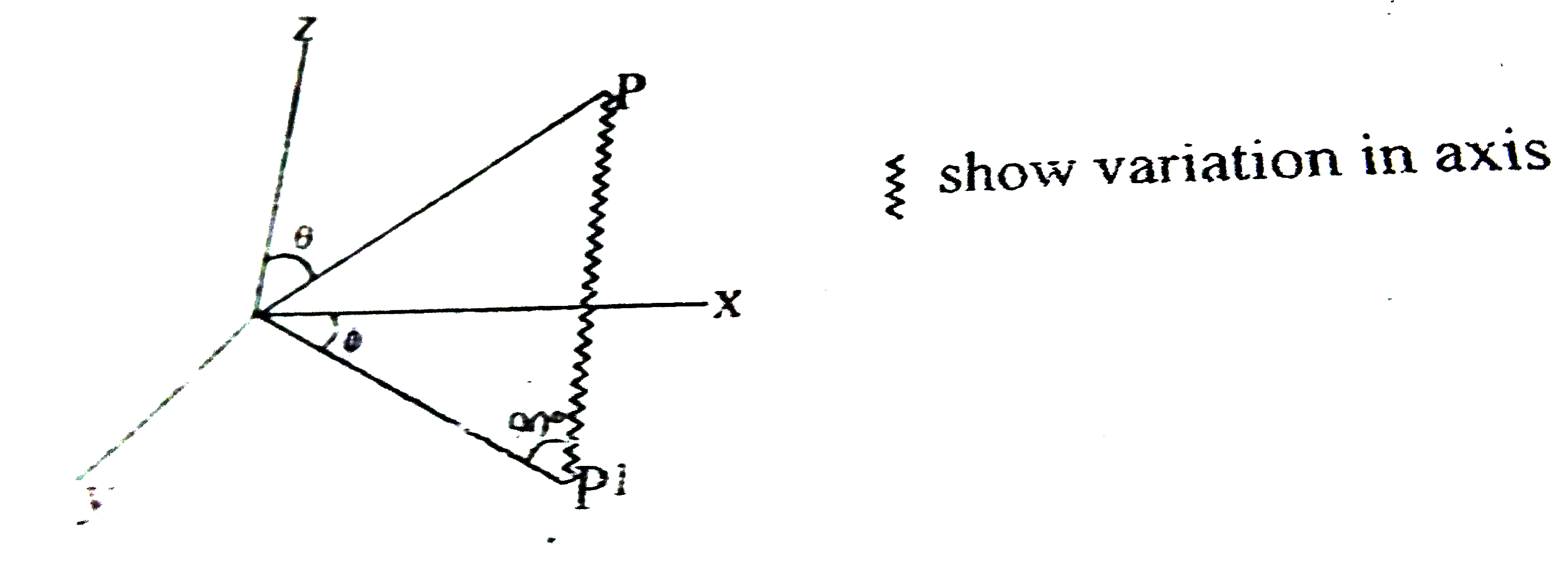
There are various types of orbitals possible, each corresponding to one of the possible combinations of quantum numbers. These orbitals are classified according to the value of n and l associated with them. In order to avoid confusion over the use of two numbers, the numerical velues of l are replaced by letters, electrons in orbitals with $l = 0$ are called s-electrons those occupying orbitals for which $l = 1$ are p-electrons and those for which $l = 2$ are called d-electrons. The numerical and alphabetical correspondences are summarized in table. Using the alphabetical notation for l, we would say that in the ground state of hydrogen atom $(n = 1, l = 0)$ we have a $1 s$ -electron, or that the electron moves in a $1 s$ -orbital. The relation of the spherical polar co-ordinates $r, θ$ and $ϕ$ to Cartesian coordinates x, y and z. To make the concept of an orbital more meaningful, it is helpful to examine the actual solution of the wave function for the one-electron atom. Because of the spherical sysmmetry of the atom, the wave functions are most simply expressed in terms of a spherical polar-coordinate system, shown in fig., which has its orbit at the nucleus. It is found that the wave function can be expressed as the product of two functions, one of which (the ''angular part'' X) depends only the angle $θ$ and $ϕ$ the other of which (the ''radial part'' R) depends only on the distance from the nucleus. Thus we have
$ϕ (r, θ, ϕ) = R (r) X (θ, ϕ)$
Angular and radial parts of hydrogen atom wave function
$(Angular part X (θ, ϕ),, Radial part R_{n, l} (r)), (X (s) = {(\frac{1}{4 π})}^{1 / 2},, R (1 s) = 2 {(\frac{z}{a_{0}})}^{3 / 2} e^{- σ / 2}), (X (p_{x}) = {(\frac{3}{4 π})}^{1 / 2} sin θ cos ϕ,, R (2 s) = \frac{1}{2 \sqrt{2}} {(\frac{z}{a_{0}})}^{3 / 2} (2 - σ) e^{- σ / 2}), (X (p_{y}) = {(\frac{3}{4 π})}^{1 / 2} sin θ sin ϕ,, R (2 p) = \frac{1}{2 \sqrt{6}} {(\frac{z}{a_{0}})}^{3 / 2} σ e^{- σ / 2}), (X (p_{z}) = {(\frac{3}{4 π})}^{1 / 2} cos θ,,), (X (d_{2}^{2}) = {(\frac{5}{16 π})}^{1 / 2} (3 {cos}^{2} θ - 1),,), (X (d_{x z}) = {(\frac{15}{4 π})}^{1 / 2} sin θ cos θ cos ϕ,, R (3 s) = \frac{1}{9 \sqrt{3}} {(\frac{z}{a_{0}})}^{3 / 2} (6 - 6 σ + σ^{2}) e^{- σ / 2}), (X (d_{y z}) = {(\frac{15}{4 π})}^{1 / 2} sin θ cos θ sin ϕ,, R (3 p) = \frac{1}{9 \sqrt{6}} {(\frac{z}{a_{0}})}^{3 / 2} (4 - σ) σ e^{- σ / 2}), (X (d_{x^{2} - y^{2}}^{2}) = {(\frac{15}{4 π})}^{1 / 2} {sin}^{2} θ cos 2 ϕ,, R (3 d) = \frac{1}{9 \sqrt{30}} {(\frac{z}{a_{0}})}^{3 / 2} σ^{2} e^{- σ / 2}), (X (d_{x y}) = {(\frac{15}{4 π})}^{1 / 2} {sin}^{2} θ sin 2 ϕ,,), (,, σ = \frac{2 Z r}{n a_{0}}, a_{0} = \frac{h^{2}}{4 π^{2} m e^{2}})$
This factrorization helps us to visualize the wave function, since it allows us to consider the angular and radial dependences separately. It contains the expression for the angular and radial parts of the one electron atom wave function. Note that the angular part of the wave function for an s-orbital it alwats the same, ${(1 / 4 π)}^{1 / 2}$ regardless of principal quantum number. It is also true that the angular dependence of the p-orbitals and of the d-orbitals is independent of principle quantum number. Thus all orbitals of given types (s, p, or d) have the same angular behavour The table shows, however, that the radial part of the wave function depends both on the principal quantum n and on the angular momentum quantum number l.
To find the wave function for a particular state, we simply multiply the appropriate angular and radial parts togather called normalized wave function.
The probability of finding an electron at a point within an atom is proportional to the square of orbital wave function, i.e., $ψ^{2}$ at that point. Thus, $ψ^{2}$ is known as probability density and always a positive quantity.
$ψ^{2} d V (or ψ^{2} . 4 π r^{2} d r)$ . represents the probability for finding electron in a small volume dV surrounding the nucleus.
The angular wave function of which orbital with not disturb by the variation with azimuthal angle only
A $1 s$ and $2 s$
B $2 p_{z}$ and $2 d_{z}^{2}$
C $2 p_{x}$ and $3 d_{z}^{2}$
D $2 p_{x}$ and $2 s$
After the faliure of Bohr atomic theory but its ability to explain to the atomic spectral a need was felt for the new model that could incorporate, the concept of stationary orbit, de Broglie concept, Heisenberg uncertainity principle. The concept that in corporate above facts is called quantum mechanics of the atomic model wave mchanical model. it includes set of quantum number and $∣ ∣ ψ^{2} ∣ ∣$ a mathematical expression of the probability of finding an electron at all points in space. This probability function is the best indication available of how the electon behaves, for as a consequence of the Uncertainity Principle, the amount we can know about the electron is limited. While quantum mechanics can tell us the exact probability of finding an electron at any two particular points, it does not tell us how the electron moves from one of these points to the other. Thus the idea of an electron orbit is lost, it is replaced with a description of where the electron is most likely to be found. This total picture of the probability of finding an electron at various points in space is called an orbital.

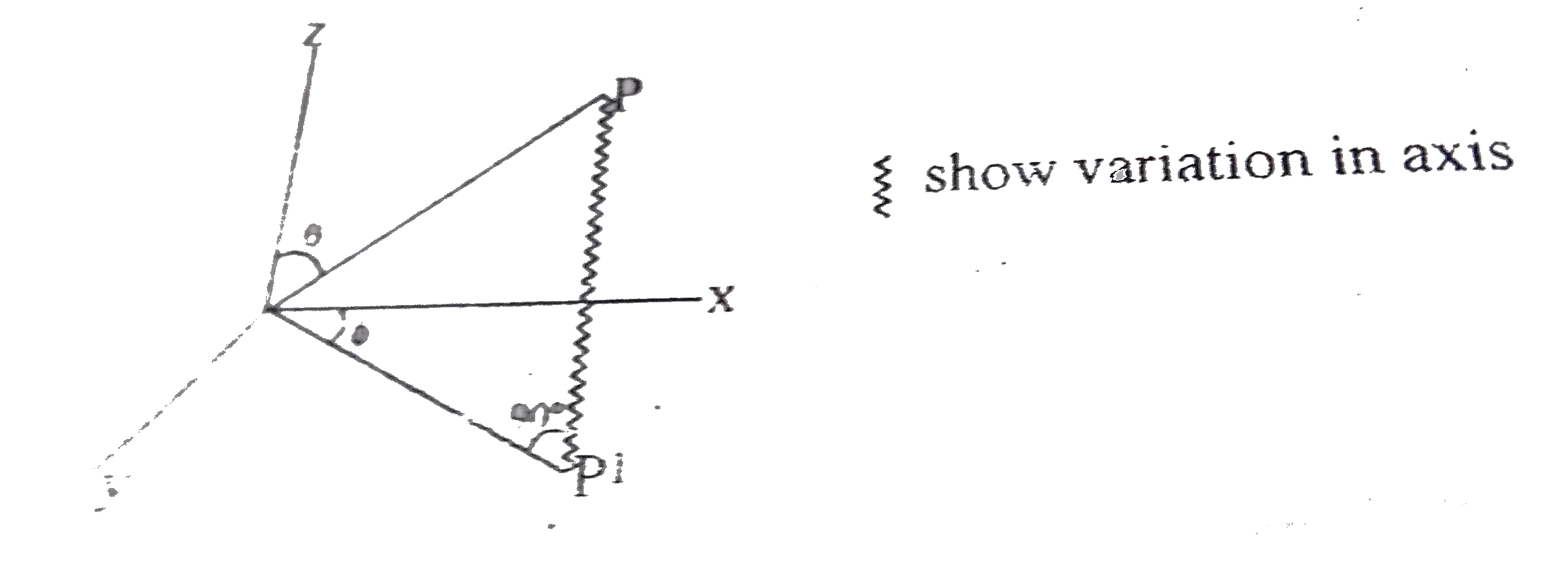
There are various types of orbitals possible, each corresponding to one of the possible combinations of quantum numbers. These orbitals are classified according to the value of n and l associated with them. In order to avoid confusion over the use of two numbers, the numerical velues of l are replaced by letters, electrons in orbitals with $l = 0$ are called s-electrons those occupying orbitals for which $l = 1$ are p-electrons and those for which $l = 2$ are called d-electrons. The numerical and alphabetical correspondences are summarized in table. Using the alphabetical notation for l, we would say that in the ground state of hydrogen atom $(n = 1, l = 0)$ we have a $1 s$ -electron, or that the electron moves in a $1 s$ -orbital. The relation of the spherical polar co-ordinates $r, θ$ and $ϕ$ to Cartesian coordinates x, y and z. To make the concept of an orbital more meaningful, it is helpful to examine the actual solution of the wave function for the one-electron atom. Because of the spherical sysmmetry of the atom, the wave functions are most simply expressed in terms of a spherical polar-coordinate system, shown in fig., which has its orbit at the nucleus. It is found that the wave function can be expressed as the product of two functions, one of which (the ''angular part'' X) depends only the angle $θ$ and $ϕ$ the other of which (the ''radial part'' R) depends only on the distance from the nucleus. Thus we have
$ϕ (r, θ, ϕ) = R (r) X (θ, ϕ)$
Angular and radial parts of hydrogen atom wave function
$(Angular part X (θ, ϕ),, Radial part R_{n, l} (r)), (X (s) = {(\frac{1}{4 π})}^{1 / 2},, R (1 s) = 2 {(\frac{z}{a_{0}})}^{3 / 2} e^{- σ / 2}), (X (p_{x}) = {(\frac{3}{4 π})}^{1 / 2} sin θ cos ϕ,, R (2 s) = \frac{1}{2 \sqrt{2}} {(\frac{z}{a_{0}})}^{3 / 2} (2 - σ) e^{- σ / 2}), (X (p_{y}) = {(\frac{3}{4 π})}^{1 / 2} sin θ sin ϕ,, R (2 p) = \frac{1}{2 \sqrt{6}} {(\frac{z}{a_{0}})}^{3 / 2} σ e^{- σ / 2}), (X (p_{z}) = {(\frac{3}{4 π})}^{1 / 2} cos θ,,), (X (d_{2}^{2}) = {(\frac{5}{16 π})}^{1 / 2} (3 {cos}^{2} θ - 1),,), (X (d_{x z}) = {(\frac{15}{4 π})}^{1 / 2} sin θ cos θ cos ϕ,, R (3 s) = \frac{1}{9 \sqrt{3}} {(\frac{z}{a_{0}})}^{3 / 2} (6 - 6 σ + σ^{2}) e^{- σ / 2}), (X (d_{y z}) = {(\frac{15}{4 π})}^{1 / 2} sin θ cos θ sin ϕ,, R (3 p) = \frac{1}{9 \sqrt{6}} {(\frac{z}{a_{0}})}^{3 / 2} (4 - σ) σ e^{- σ / 2}), (X (d_{x^{2} - y^{2}}^{2}) = {(\frac{15}{4 π})}^{1 / 2} {sin}^{2} θ cos 2 ϕ,, R (3 d) = \frac{1}{9 \sqrt{30}} {(\frac{z}{a_{0}})}^{3 / 2} σ^{2} e^{- σ / 2}), (X (d_{x y}) = {(\frac{15}{4 π})}^{1 / 2} {sin}^{2} θ sin 2 ϕ,,), (,, σ = \frac{2 Z r}{n a_{0}}, a_{0} = \frac{h^{2}}{4 π^{2} m e^{2}})$
This factrorization helps us to visualize the wave function, since it allows us to consider the angular and radial dependences separately. It contains the expression for the angular and radial parts of the one electron atom wave function. Note that the angular part of the wave function for an s-orbital it alwats the same, ${(1 / 4 π)}^{1 / 2}$ regardless of principal quantum number. It is also true that the angular dependence of the p-orbitals and of the d-orbitals is independent of principle quantum number. Thus all orbitals of given types (s, p, or d) have the same angular behavour The table shows, however, that the radial part of the wave function depends both on the principal quantum n and on the angular momentum quantum number l.
To find the wave function for a particular state, we simply multiply the appropriate angular and radial parts togather called normalized wave function.
The probability of finding an electron at a point within an atom is proportional to the square of orbital wave function, i.e., $ψ^{2}$ at that point. Thus, $ψ^{2}$ is known as probability density and always a positive quantity.
$ψ^{2} d V (or ψ^{2} . 4 π r^{2} d r)$ . represents the probability for finding electron in a small volume dV surrounding the nucleus.
The electron probility density for $1 s$ -orbital best represented by the relation.
A $\frac{1}{2 \sqrt{π}} {(\frac{Z}{a_{0}})}^{3 / 2} \times e^{\frac{r}{a_{0}}}$
B $\frac{1}{π} {(\frac{Z}{a_{0}})}^{3} \times e^{- \frac{2 z r}{a_{0}}}$
C $\frac{1}{π} {(\frac{Z}{a_{0}})}^{3 / 2} \times e^{\frac{r}{a_{0}}}$
D $\frac{2}{π} {(\frac{Z}{a_{0}})}^{3} \times e^{- \frac{2 z r}{a_{0}}}$
Read the passage carefully and select the best answer to each question out of the given four alternatives.
Transactional Analysis has the triangle of PAC. P means parent, A means adult, C means child. These are your three layers, as if you are a three-storeyed building. The first floor is that of the child, the second floor is that of the parent, the third floor is that of the adult. All three exist together. This is your inner triangle and conflict. Your child says one thing, your parent says something else, and your adult, tional mind says something else. The child says ‘enjoy’. For the child, this moment is the only moment, he has no other considerations. The child is spontaneous, but naware of the consequences — unaware of past, unaware of future. He lives in the moment. He enjoys — but his enjoyment is not creative, cannot be creative. He delights — but life cannot be lived only through delight. You cannot remain a child forever. You will have to learn many things because you are not alone here....The child has to be disciplined — and t’s where the parent comes in. The parental voice in you is the voice of the society, culture, civilization, the voice that makes you capable of living in a world where you are not alone —where there are many individuals with conflicting ambitions, where there is much struggle for survival, where there is much conflict. The parental voice is that of caution. It makes you civilized. The word ‘civil’ is good. It means one who has become capable of living in a city, who has become capable of being a member of a group, of a society. It is needed. And then there is the third voice within you, the third layer, when you have become adult and you are no longer controlled by your parents, your own reason has come of age, you can think on your own. And these three layers are continuously fighting. The child says one thing, the parent says just the opposite, and the reason may say something totally different. There is no necessity that your adult mind agrees with your parents. Many times you find them very dogmatic, superstitious, believing in foolish things, irrational ideologies. Your parent says do it, your adult says it is not worth doing, and your child goes on pulling you somewhere else. This is the triangle within you.
According to the passage, you are not capable of being a member of a group, of a society until you become _______
AParent
BCivil
CDogmatic
DAuditious

Rashid is studying in class V. He can classify various types of triangles in different categories but has difficulty in understanding the abstract proof for the sum of three angles in a triangle to be always 180. According to Piaget Cognitive Theory, Rashid is at:

The correct Answer is:A

Similar Questions

Knowledge Check

CTET MASTER-EVS CONTENT AND PEDAGOGY-MULTIPLE CHOICE QUESTIONS