Metallic gold crystallizes in the fcc lattice.
The length of the cubic unit cell is a=4.242A.
a. What is the closest distance between gold atoms?
b. How many "nearest neighbours" does each gold atom have at the distance calculated in (a)?
(c) What is the density of gold? (Aw of Au =197.0gmol−1)
d. Prove that the packing factor for gold is 0.74.
Solution in Kannada
In fc c, Z(eff)=4.
For fcc, atomic radius (r)=a2√2
a. Closest distance two Au atoms =2r
=2×a2√2=a√2=4.242√2=4.2421.414=3.0Å
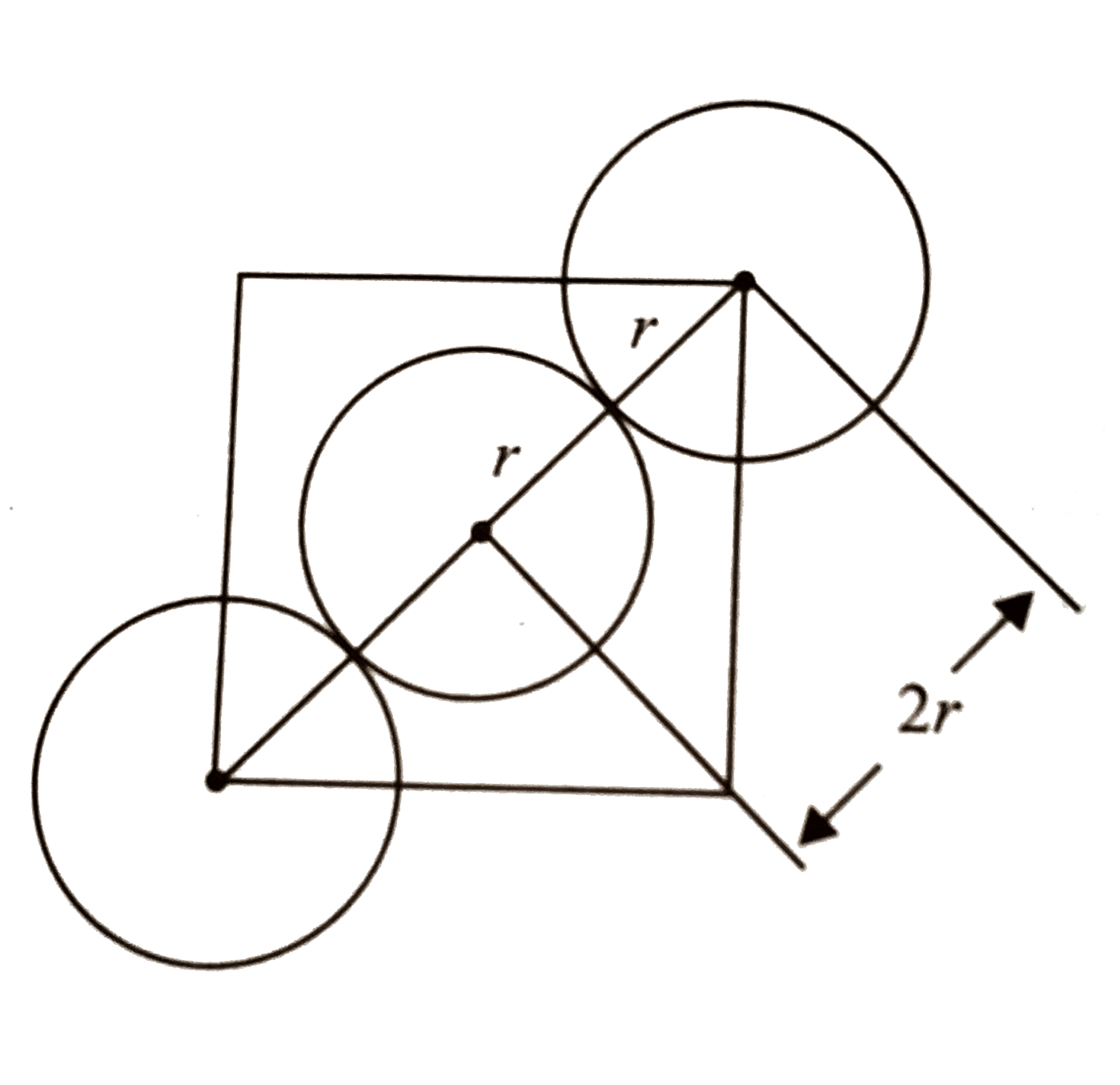
As the coordination number of fc c =12.
So there are 12 nearest neighbours in all, the number expected for a close-packed structure.
c. Density =ρ=Zeff×AwNA×a3
=4×197g6×1023×(3.0×10−8cm)3
=19.4gcm−3
d. Packing factor for fcc lattice =√26π=0.7404
Similar Questions
Metallic gold crystallises in fcc lattice. The length of the cubic unit cell is a = 4.07 Å (a) What is the closest distance between gold atoms. (b) How many "nearest neighbours" does each gold atom have at the distance calculated in (a). (c) What is the density of gold ? (d) Prove that the packing fraction of gold is 0.74.
View SolutionMetallic gold crystallizes in the face centered cubic lattice. What is the approximate number of unit cells in 2.0 g of gold ? (Atomic mass of gold is 197 amu)
View SolutionMetallic gold crystallizes in fcc lattice. The length of the cubic unit cell is 4.07 Å (a) What is the closest distance between gold atoms ? (b) How many 'nearest neighbours' does each gold atom have at the distance calculated in (a) ? (c ) What is the density of gold ? (d) Prove that the packing fraction of gold is 0.74.
View SolutionCalculate the approximate number of unit cells present in 1 g of gold. When gold crystallizes in the fcc lattice (Au = 197).
View SolutionMetallic gold crystallises in face centred cubic lattice with edge-length 4.07Å. Closest distance between gold atoms is:
View SolutionMetallic gold crystallises in face centred cubic lattice with edge-length 4.07Å. Closest distance between gold atoms is:
View SolutionGold metal crystallizes in a face-centred cubic cell (fcc). Determine the density of gold. (Atomic mass of gold = 197u, atomic radius of 0.144 nm, N_A = 6.012xx10^23 mol^-1 ).
View SolutionMetallic gold crystallizes in ccp lattice. The length of the cubic unit cell is 4.242 A^@ . The closest distance between two atoms of gold
View Solution