Question

Draw a two-dimesnsional haxagonal lattice. Try to visualize the possibility of pentagonal two-dimensional lattice.

Explanation

Three regular haxagons intersect at one point. So, in this two-dimensional lattice, this lattice point is shared by three unit cells.

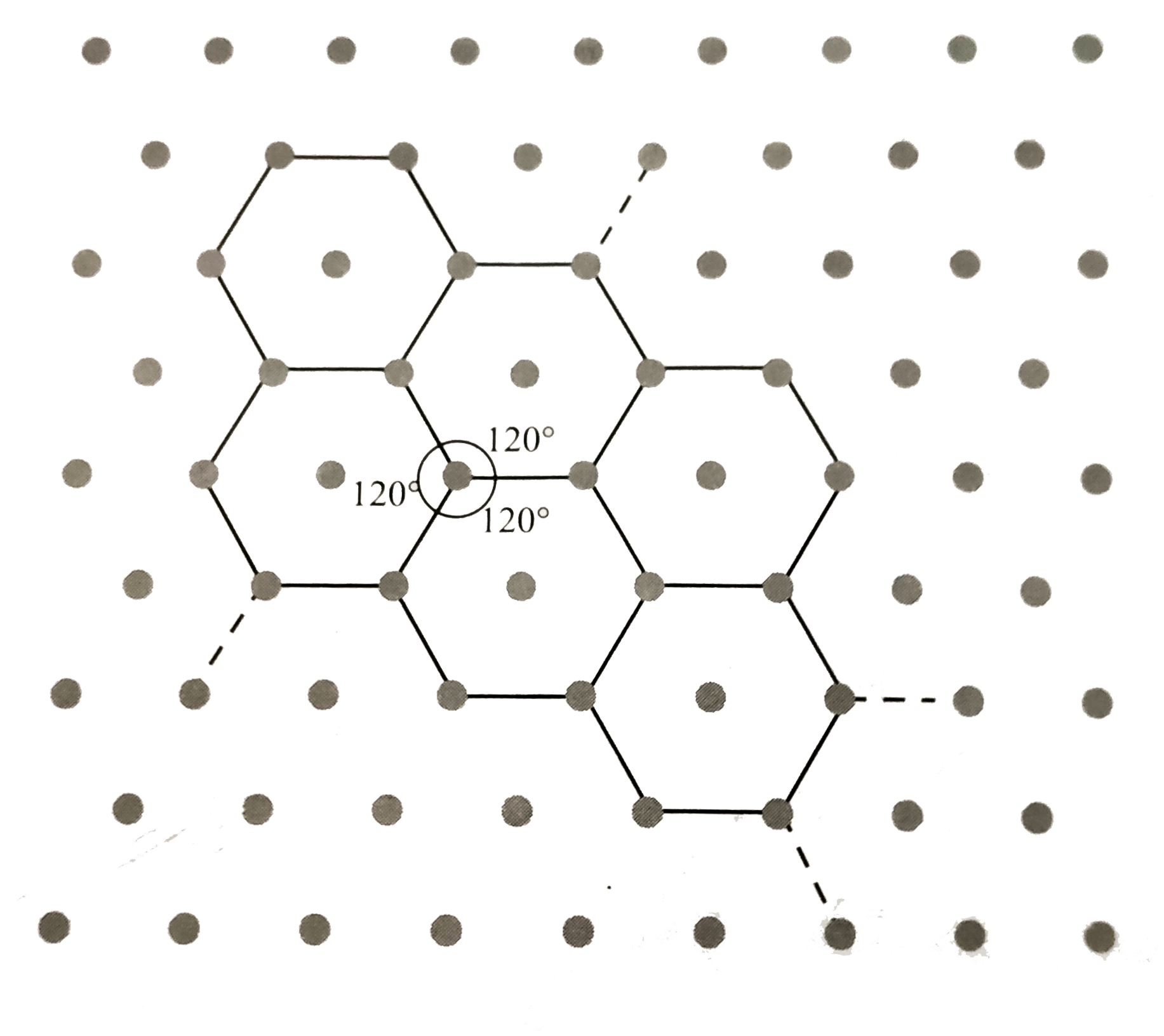
So, the effective number of lattice point per unit cell `= 6 xx ((1)/(3)) + 1 xx (1) = 3`.
A regular pentagon has an interior angle of `108^@`, pentagons cannot be made to meet at a point bearing a constant angle to one another. Hence, a pentagonal lattice is not possible. On the other hand, a square or a hexagonal two-dimensional lattice is possible as their internal angles add up to give `360^(@)`.