A wire of mass and length is bent in the form of circular ring. The moment of inertia of the ring about its axis is
The correct Answer is:A
Step by step video, text & image solution for A wire of mass m and length l is bent in the form of circular ring. The moment of inertia of the ring about its axis is by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Similar Questions
A thin uniform wire of mass m and length l is bent into to shape of a semicircle. The moment of inertia of that wire about an axis passing through its free ends is
View SolutionA thin wire of mass m and length l is bent in the form of a ring . Moment of inertia of that ring about an axis passing through its centre and perpendicular to its through its centre and perpendicular to its plane is
View Solution
Knowledge Check
- Question 1 - Select One
A wire of mass 'm' and length 'l' is bent in the form of a circular ring. The moment of inertia of the ring about its axis is-
Aml2B1ml22π2Cml24πDml28π2 - Question 2 - Select One
A wire of mass m and length l is bent in the form of circular ring. The moment of inertia of the ring about its axis is
AMl4π2BMl2πCMl4πDMl24π2 - Question 3 - Select One
A wire of mass m and length l is bent in the form of a quarter circle. The moment of the inertia of the wire about an axis is passing through the centre of the quarter circle is approximately
A0.6ml2Bml2C0.2ml2D0.4ml2
A thin rod of mass M and length L is bent into a circular ring. The expression for moment of inertia of ring about an axis passing through its diameter is
View SolutionThe moment of inertia of semicircular ring about its centre is
View SolutionA thin wire of mass M and length L is turned into a ring. The moment of inertia about its axis will be:
View SolutionA thin wire of length l and mass m is bent in the form of a semicircle as shown in the figure. Its moment of inertia about an axis joining its free ends will be
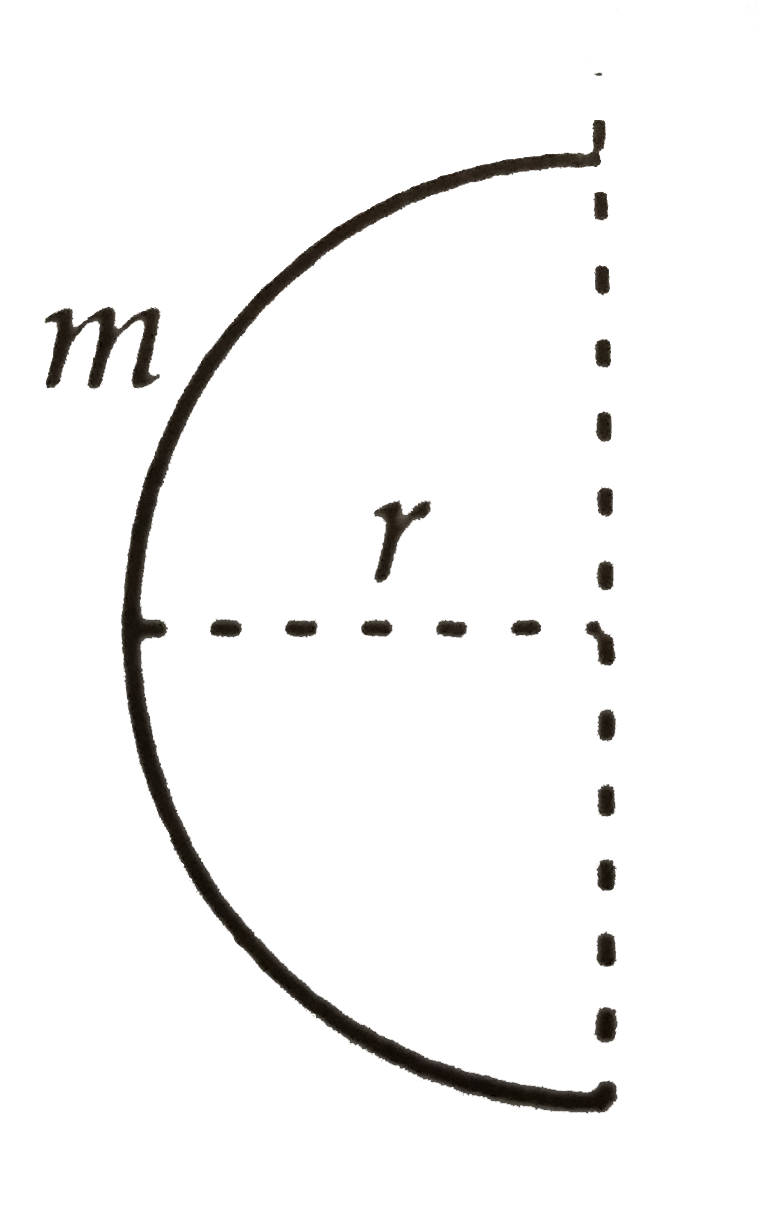 View Solution
View SolutionA thin wire of length l and mass m is bent in the form of a semicircle as shown in the figure. Its moment of inertia about an axis joining its free ends will be
 View Solution
View Solution
