Four wires each of same length diameter and material are connected to each other to form a square. If the resistance of each wire is R then equivalent resistance across the opposite corners is
R
R/2
R/4
none of these
The correct Answer is:A
To find the equivalent resistance across the opposite corners of a square formed by four wires, we can follow these steps:
Step 1: Understand the Configuration
We have four wires connected to form a square. Each wire has the same resistance R. We need to find the equivalent resistance between two opposite corners of the square.
Step 2: Identify the Resistors in the Circuit
Label the corners of the square as A, B, C, and D. The resistances can be represented as follows:
- Resistance R1 between A and B
- Resistance R2 between B and C
- Resistance R3 between C and D
- Resistance R4 between D and A
Step 3: Determine the Series and Parallel Combinations
When looking for the equivalent resistance between corners A and B:
- The resistances R1 (A to B) and R3 (C to D) are in series.
- The resistances R2 (B to C) and R4 (D to A) are also in series.
Step 4: Calculate the Resistance in Series
For the resistors in series:
- The total resistance of R1 and R4 (A to B and D to A) is:
RAB=R+R=2R
- The total resistance of R2 and R3 (B to C and C to D) is:
RCD=R+R=2R
Step 5: Combine the Series Resistances in Parallel
Now, we have two resistances RAB=2R and RCD=2R in parallel between A and B:
1Req=1RAB+1RCD=12R+12R
Step 6: Simplify the Parallel Resistance
Calculating the above expression:
1Req=1+12R=22R=1R
Thus, the equivalent resistance Req is:
Req=R
Final Answer
The equivalent resistance across the opposite corners A and B is R.
---
We have four wires connected to form a square. Each wire has the same resistance R. We need to find the equivalent resistance between two opposite corners of the square.
Label the corners of the square as A, B, C, and D. The resistances can be represented as follows:
- Resistance R1 between A and B
- Resistance R2 between B and C
- Resistance R3 between C and D
- Resistance R4 between D and A
When looking for the equivalent resistance between corners A and B:
- The resistances R1 (A to B) and R3 (C to D) are in series.
- The resistances R2 (B to C) and R4 (D to A) are also in series.
For the resistors in series:
- The total resistance of R1 and R4 (A to B and D to A) is:
RAB=R+R=2R
- The total resistance of R2 and R3 (B to C and C to D) is:
RCD=R+R=2R
Now, we have two resistances RAB=2R and RCD=2R in parallel between A and B:
1Req=1RAB+1RCD=12R+12R
Calculating the above expression:
1Req=1+12R=22R=1R
Thus, the equivalent resistance Req is:
Req=R
The equivalent resistance across the opposite corners A and B is R.
Similar Questions
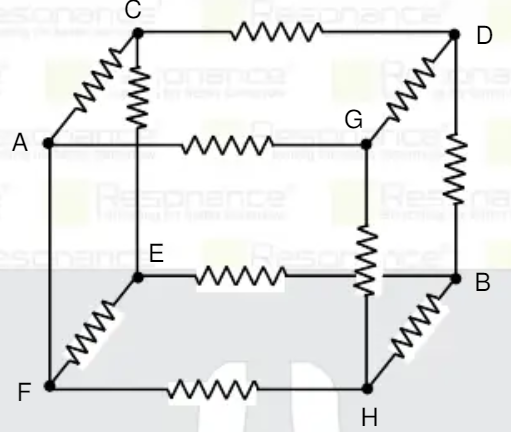
Twelve wires of equal length and same cross-section are connected in the form of a cube. If the resistance of each of the wires is R, and the effective resistance between the two diagonal ends is Re, then the ratio RRe is equal to __.
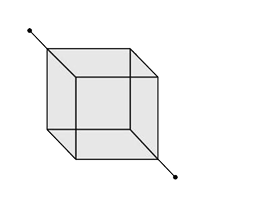
View SolutionA cube made up of wire each of resistance R. The find equivalent resistance across its diagnol
View Solution
Knowledge Check
Four wires each of same length, diameter and material are connected to each other to form a square. If the resistance of each wire is R, then equivalent resistance across the opposite comers is
ARBR/2CR/4DNone of the theseResistance of each resistor is R. Then the equivalent resistance across A and B is
 A59RB49RCR9D79R
A59RB49RCR9D79RIn the circuit shown in figure resistance of each wire is r. Net resistance across
 Aa and b is 1325rBb and c is 1950rCd and e is 725rDf and g is 1150r
Aa and b is 1325rBb and c is 1950rCd and e is 725rDf and g is 1150r
Four resistances, each of 10Ω, are connected to form a square as shown in (Fig. 3.52), find the equivalent resistance between the opposite corners AandC.
 .
.
View SolutionTwelve wires of equal length and same cross-section are connected in the form of a cube. If the resistance of each of the wires is R , then the effective resistance between the two diagonal ends would be

View Solution
In the network shown, each resistance is equal to R. The equivalent resistance between diagonally opposite corners is
View Solution10 wires (same length, same area, same material) are connected in parallel and each has 1Ω resistance, then the equivalent resistance will be
View SolutionIn the figure shown, the equivalent resistance across BC if each resistance is 28 Ω is
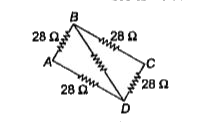
View Solution
