An object is kept at a distance of 60 cm from a concave mirror. For getting a magnification of 12, focal length of the concave mirror required is
20 cm
40 cm
- 20 cm
30 cm
The correct Answer is:C
To solve the problem step by step, we will use the mirror formula and the magnification formula.
Step 1: Understand the given information
- The object distance (U) is given as 60 cm. Since it is a concave mirror and the object is real, we take U as -60 cm.
- The magnification (m) is given as 12.
Step 2: Use the magnification formula
The magnification (m) for mirrors is given by the formula:
m=−VU
Where:
- V is the image distance
- U is the object distance
Substituting the known values:
12=−V−60
Step 3: Solve for V
Rearranging the equation to find V:
12=V60
Cross-multiplying gives:
V=60×12=30 cm
Since the image is formed on the same side as the object in a concave mirror, we take V as -30 cm.
Step 4: Use the mirror formula
The mirror formula is given by:
1F=1V+1U
Substituting the values of V and U:
1F=1−30+1−60
Step 5: Calculate 1F
Finding a common denominator (which is 60):
1F=−260+−160=−360
Thus:
1F=−120
Step 6: Solve for F
Taking the reciprocal gives:
F=−20 cm
Final Answer
The focal length of the concave mirror required is −20 cm.
---
- The object distance (U) is given as 60 cm. Since it is a concave mirror and the object is real, we take U as -60 cm.
- The magnification (m) is given as 12.
The magnification (m) for mirrors is given by the formula:
m=−VU
Where:
- V is the image distance
- U is the object distance
12=−V−60
Rearranging the equation to find V:
12=V60
Cross-multiplying gives:
V=60×12=30 cm
Since the image is formed on the same side as the object in a concave mirror, we take V as -30 cm.
The mirror formula is given by:
1F=1V+1U
Substituting the values of V and U:
1F=1−30+1−60
Finding a common denominator (which is 60):
1F=−260+−160=−360
Thus:
1F=−120
Taking the reciprocal gives:
F=−20 cm
The focal length of the concave mirror required is −20 cm.
Similar Questions
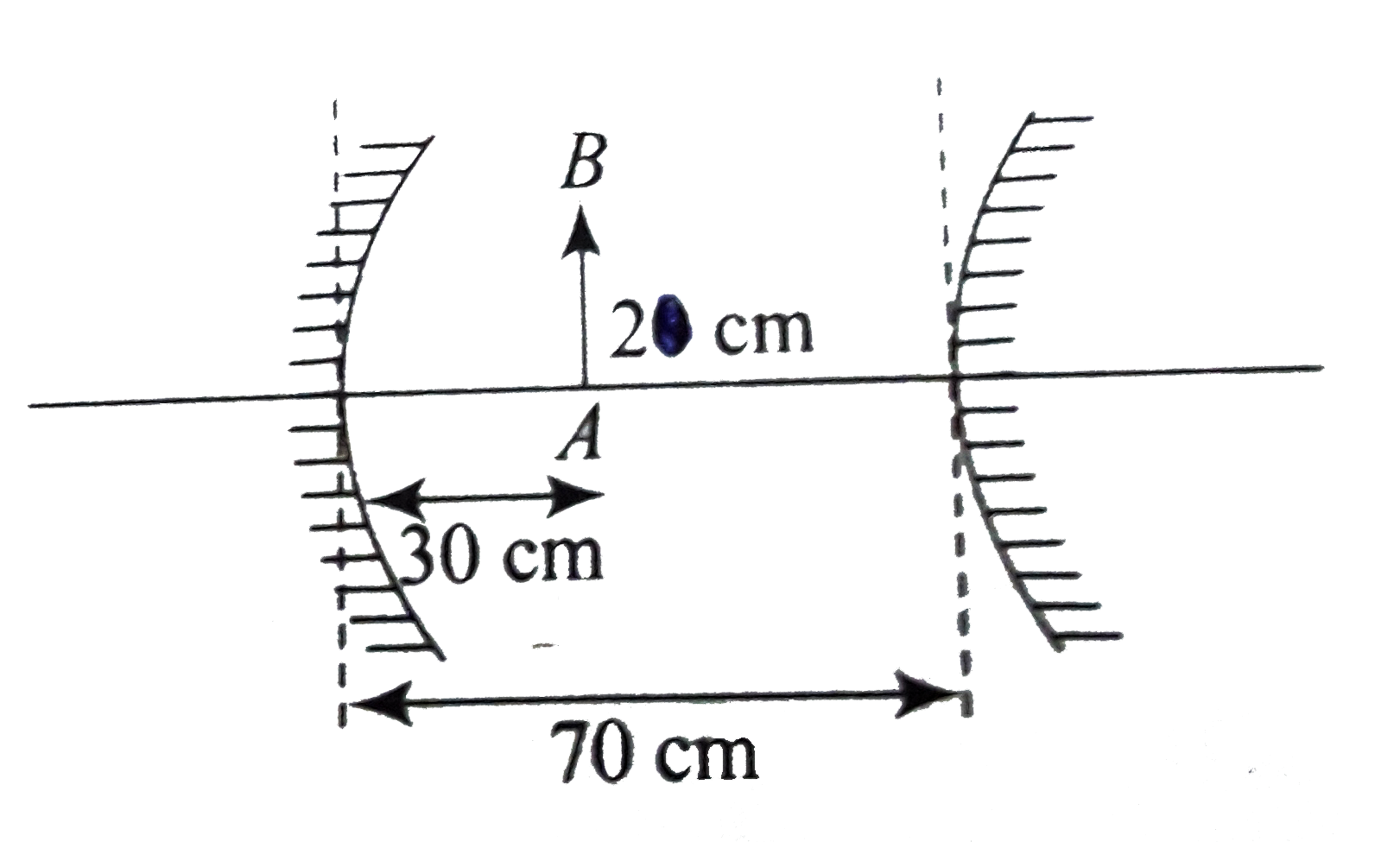
A concave mirror and a convex mirror of focal lengths 10cm and 15cm are places at a distance of 70cm. An object AB of height 2cm is places at a distance of 30cm from the concave mirror. First ray is incident on the concave mirror then on the convex mirror. Find size, position, and nature of the image.
View SolutionAn object is placed at a distance of 40 cm in front of a concave mirror of focal length 20 cm. The image produced is
View Solution
Knowledge Check
Focal length of a concave mirror is
ApositiveBnegativeCdepends on the position of the objectsDdepends on the position of imageAn object of length 2.5 cm is placed at a distance of 1.5 f from a concave mirror where f is the magnitude of the focal length of the mirror The length of the object is perpendicular to the principle axis. The length of the image is:
A5 cm, erectB10 cm, erectC15 cm, erectD5 cm, invertedAn object is placed at a distance of 15 cm from a concave mirror and its real image is formed at 30 cm in front of that mirror. The focal length of the mirror is
A+20 cmB−20 cmC−10 cmD+10 cm
An object is placed at a distance of 10 cm from a concave mirror. When the distance of object from the mirror is decreased to 6 cm, the image gets 2 times magnified than that in first case. Calculate the focal length of the mirror.
View SolutionAn object placed at 20cm in front of a concave mirror produces three times magnified real image. What is the focal length of the concave mirror?
View SolutionAn object of height 1.5 cm situated at a distance of 15 cm from a concave mirror . The concave mirror formus its real image of height 3.0 . The focal length of concave mirror will be.
View SolutionAn object is placed at a distance of 30 cm from a concave mirror and its real image is formed at a distance of 30 cm from the mirror. The focal length of the mirror is
View SolutionAn object is placed at a distance of 20 cm from the pole of a concave mirror of focal length 10 cm. The distance of the image formed is
View Solution
