Four balls A,B,C and D displace 10mL,24mL,15mL and 12mL of a liquid respectively when immersed completely the ball which will undergo the maximum apparent loss in weight will be
A
B
C
D
The correct Answer is:B
To solve the problem of which ball will undergo the maximum apparent loss in weight when immersed in a liquid, we can follow these steps:
1. Understanding Apparent Loss in Weight:
The apparent loss in weight of an object submerged in a fluid is equal to the weight of the fluid displaced by the object. According to Archimedes' principle, the more fluid displaced, the greater the buoyant force acting on the object, and thus the greater the apparent loss in weight.
2. List the Displaced Volumes:
We have four balls A, B, C, and D with the following volumes of liquid displaced:
- Ball A displaces 10 mL
- Ball B displaces 24 mL
- Ball C displaces 15 mL
- Ball D displaces 12 mL
3. Identify the Maximum Volume Displaced:
We need to determine which ball displaces the maximum volume of liquid. From the data given:
- A: 10 mL
- B: 24 mL
- C: 15 mL
- D: 12 mL
The maximum volume displaced is 24 mL by Ball B.
4. Conclusion:
Since Ball B displaces the maximum volume of liquid (24 mL), it will experience the maximum apparent loss in weight when immersed in the liquid.
Final Answer:
The ball which will undergo the maximum apparent loss in weight is Ball B.
---
The apparent loss in weight of an object submerged in a fluid is equal to the weight of the fluid displaced by the object. According to Archimedes' principle, the more fluid displaced, the greater the buoyant force acting on the object, and thus the greater the apparent loss in weight.
We have four balls A, B, C, and D with the following volumes of liquid displaced:
- Ball A displaces 10 mL
- Ball B displaces 24 mL
- Ball C displaces 15 mL
- Ball D displaces 12 mL
We need to determine which ball displaces the maximum volume of liquid. From the data given:
- A: 10 mL
- B: 24 mL
- C: 15 mL
- D: 12 mL
Since Ball B displaces the maximum volume of liquid (24 mL), it will experience the maximum apparent loss in weight when immersed in the liquid.
The ball which will undergo the maximum apparent loss in weight is Ball B.
Similar Questions
A heavy ball weighing 5 N displaces 100 ml of water when immersed in water. Calculate the apparent weight of the ball in water.
View SolutionTwo acids A and B titrated separately each time with 25 mL of N Na2CO3 solution and require 10 mL and 40 mL respectively for complete neutralisation. What volume of A and B would you mix to produce one litre of normal acid solution ?
View Solution
Knowledge Check
Four balls,A,B,C,D displace 10 mL ,24 mL,15 mL, and 12 mL of a liquid respectively ,when immersed completely.The ball which will undergo the maximum apparent loss in weight will be :
AABBCCDDWhen two balls, one of iron and the other of aluminium, are completely immersed in strong salty water they undergo an equal loss in weight. This shows that iron and aluminium balls have:
Athe same densitiesBthe same massesCthe same volumesDthe same weightsFor an allotropic change:
A(s)→B(s),δG∘400=20kJ/mole
If molar volume A and B are 12mL/mole and 10mL/mole respectively then calculate approximate pressure at which the two allotropes will be at equillibrium at 400K:A105PaB2×104PaC100PaD1010Pa
An aluminium ball is fully immersed in distilled water, well water, sea water and inland lake water, one by one. The aluminium ball will appear to suffer the maximum loss in weight when immersed in:
View SolutionWhen 10 ml of hydrogen and 12.5ml of chlorine are allowed to react the final mixture contains under the same conditions
View SolutionWhen 10 ml of hydrogen and 12.5 ml of chlorine are allowed to react the final mixture contains under the same conditions
View SolutionTwo inflated ballons I and II (thin skin) having volume 600 mL and 1500 mL at 300 K are taken as shown in diagram. If maximum volume of inner and outer balloons are 800 mL and 1800 mL respectively then find the balloon which will burst first on gradual heating.
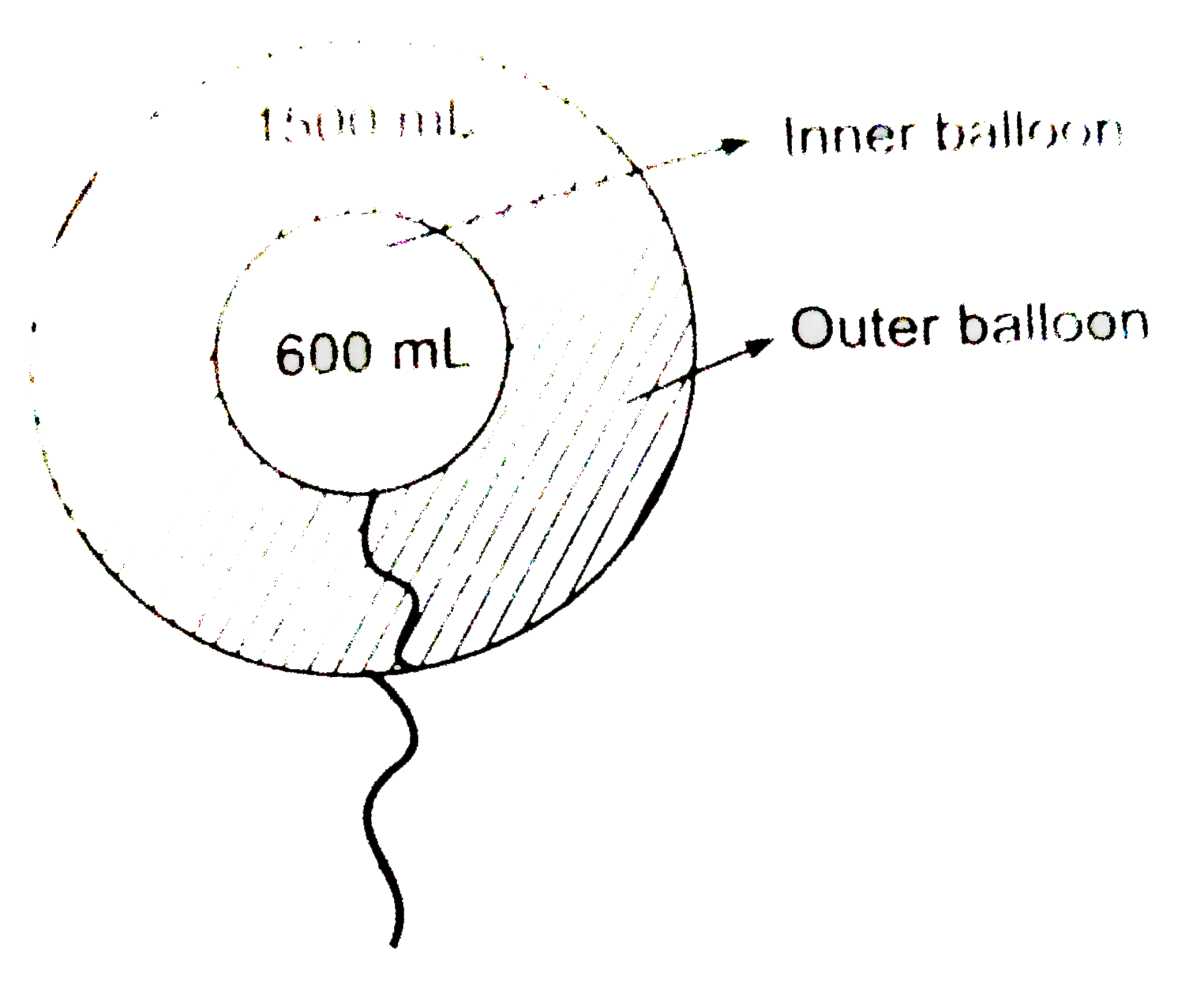
View Solution0.45 g of a dibasic acid is completely netralised with 100 ml N10 NaOH . The molecular weight of acid is
View Solution