→F is the force on the arm of a square toop suspended in a uniform mdgnetic field. Net : force on remaining arnis is :
−→F
→F
−3→F
3→F
The correct Answer is:A
To solve the problem, we need to analyze the forces acting on the arms of a square loop suspended in a uniform magnetic field.
1. Understanding the Setup:
- We have a square loop suspended in a uniform magnetic field.
- The loop carries a current, which interacts with the magnetic field to produce forces on the arms of the loop.
2. Identifying the Forces:
- The magnetic force on a current-carrying conductor in a magnetic field is given by the formula:
→F=I(→L×→B)
where I is the current, →L is the length vector of the conductor, and →B is the magnetic field.
3. Analyzing the Arms Parallel to the Field:
- For the two arms of the loop that are parallel to the magnetic field, the angle between the current direction and the magnetic field is 0 degrees.
- Therefore, the force on these arms is:
→Fparallel=I(→L×→B)=0
This is because the cross product of two parallel vectors is zero.
4. Analyzing the Remaining Arms:
- The other two arms of the square loop are perpendicular to the magnetic field.
- The force on these arms can be calculated using the same formula. Since the angle is 90 degrees, the force will be:
→Fperpendicular=ILB
- If we denote the force on one of these arms as →F, then the force on the other arm will be equal in magnitude but opposite in direction.
5. Net Force on the Remaining Arms:
- The total force on the two arms that are perpendicular to the magnetic field will be:
→Fnet=→F+(−→F)=0
- However, since we are interested in the net force on the remaining arms, we can express it as:
Net force on remaining arms=−→F
6. Conclusion:
- The net force on the remaining arms of the square loop is given by:
Net force on remaining arms=−→F
Final Answer:
The net force on the remaining arms is −→F.
- We have a square loop suspended in a uniform magnetic field.
- The loop carries a current, which interacts with the magnetic field to produce forces on the arms of the loop.
- The magnetic force on a current-carrying conductor in a magnetic field is given by the formula:
→F=I(→L×→B)
where I is the current, →L is the length vector of the conductor, and →B is the magnetic field.
- For the two arms of the loop that are parallel to the magnetic field, the angle between the current direction and the magnetic field is 0 degrees.
- Therefore, the force on these arms is:
→Fparallel=I(→L×→B)=0
This is because the cross product of two parallel vectors is zero.
- The other two arms of the square loop are perpendicular to the magnetic field.
- The force on these arms can be calculated using the same formula. Since the angle is 90 degrees, the force will be:
→Fperpendicular=ILB
- If we denote the force on one of these arms as →F, then the force on the other arm will be equal in magnitude but opposite in direction.
- The total force on the two arms that are perpendicular to the magnetic field will be:
→Fnet=→F+(−→F)=0
- However, since we are interested in the net force on the remaining arms, we can express it as:
Net force on remaining arms=−→F
- The net force on the remaining arms of the square loop is given by:
Net force on remaining arms=−→F
The net force on the remaining arms is −→F.
Topper's Solved these Questions
- SAMPLE PAPER 7BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 7EXERCISE - SECTION-B
24 Videos
- SAMPLE PAPER 7BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 7EXERCISE - SECTION-C
6 Videos
- SAMPLE PAPER 6BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 6EXERCISE - Section-C
6 Videos
- SAMPLE PAPER 9 BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 9 EXERCISE - SECTION - C
3 Videos
Similar Questions
Knowledge Check
What is the net force on the square coil?
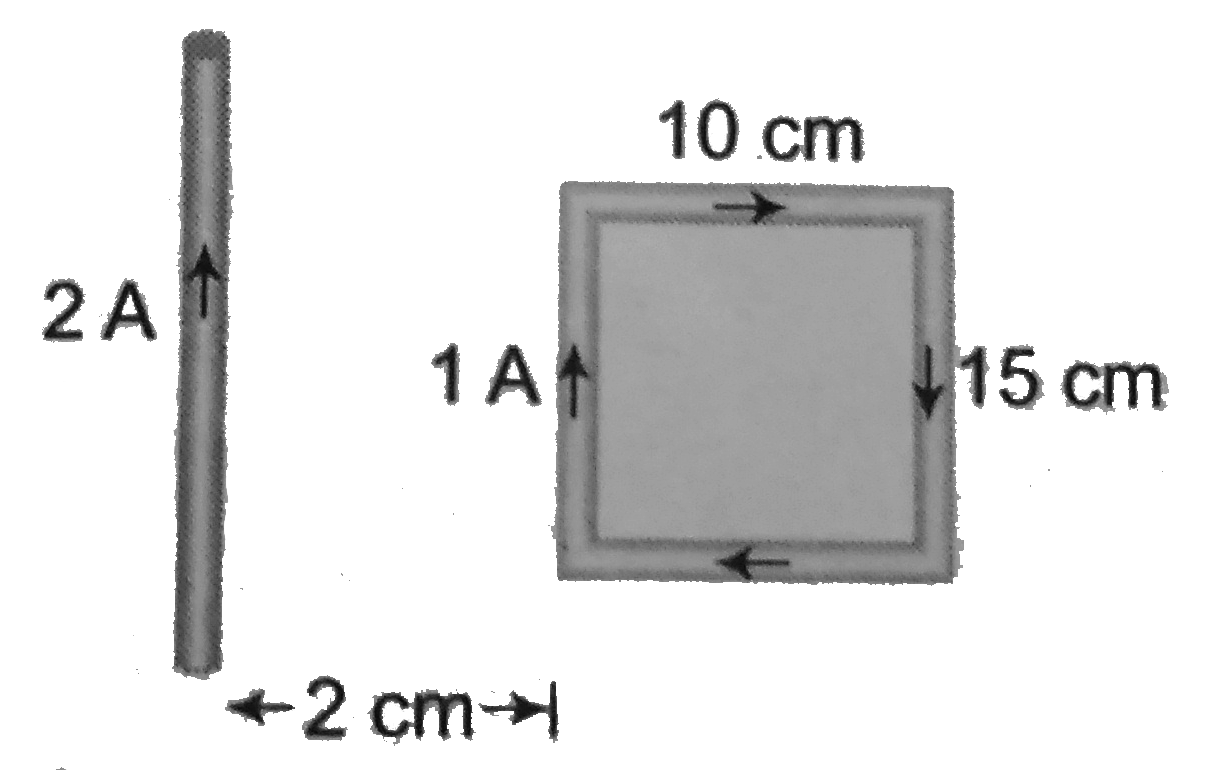A25×10−7N moving towards wireB35×10−7N moving away from wireC35×10−7N moving towards wireD35×10−7N moving away from wireWhat is the net force on the rectangular coil
A25×10−7 N moving towards wireB25×10−7 N moving away from wireC35×10−7 N moving towards wireD25 xx10^(-7)N moving away from wireThe lines of force of uniform magnetic field
Amust be convergentBmust be divergentCmust be parallel to each otherDintersect
