Is it necessary condition for a Gaussian surface to have a symmetrical area as per gauss law?
No
Yes
Sometimes
Can't say
The correct Answer is:A
To determine whether it is a necessary condition for a Gaussian surface to have a symmetrical area as per Gauss's law, we can analyze the principles behind Gauss's law and the implications of symmetry.
1. Understanding Gauss's Law: Gauss's law states that the electric flux (Φ_E) through a closed surface is proportional to the charge (Q_enc) enclosed within that surface. Mathematically, it is expressed as:
ΦE=∮E⋅dA=Qencϵ0
where E is the electric field, dA is the differential area vector, and ϵ0 is the permittivity of free space.
2. Choosing a Gaussian Surface: The choice of a Gaussian surface is crucial for simplifying calculations. A symmetrical surface (like a sphere, cylinder, or plane) is often chosen because it allows for uniformity in the electric field across the surface.
3. Electric Field Uniformity: For the integral ∮E⋅dA to be simplified, the electric field E must be constant over the surface. This is typically achieved when the Gaussian surface is symmetrical with respect to the charge distribution.
4. Implications of Asymmetry: If the Gaussian surface is not symmetrical, the electric field may vary in magnitude and direction across the surface. This variation complicates the integration, making it difficult or impossible to apply Gauss's law effectively.
5. Conclusion: Therefore, while it is not strictly necessary for a Gaussian surface to be symmetrical for Gauss's law to be applied, symmetry greatly simplifies the application of the law and is often a preferred condition for ease of calculation. In many practical scenarios, symmetrical surfaces lead to straightforward solutions.
Final Answer:
It is not a strict necessity for a Gaussian surface to have a symmetrical area as per Gauss's law, but symmetry is highly advantageous for simplifying calculations and ensuring uniform electric field conditions.
ΦE=∮E⋅dA=Qencϵ0
where E is the electric field, dA is the differential area vector, and ϵ0 is the permittivity of free space.
It is not a strict necessity for a Gaussian surface to have a symmetrical area as per Gauss's law, but symmetry is highly advantageous for simplifying calculations and ensuring uniform electric field conditions.
Topper's Solved these Questions
- SAMPLE PAPER 6Book:EDUCART PUBLICATIONChapter:SAMPLE PAPER 6Exercise:Section-B
Explore 24 Videos
- SAMPLE PAPER 6Book:EDUCART PUBLICATIONChapter:SAMPLE PAPER 6Exercise:Section-C
Explore 6 Videos
- SAMPLE PAPER 5Book:EDUCART PUBLICATIONChapter:SAMPLE PAPER 5Exercise:SECTION - C
Explore 6 Videos
- SAMPLE PAPER 7Book:EDUCART PUBLICATIONChapter:SAMPLE PAPER 7Exercise:SECTION-C
Explore 6 Videos
Similar Questions
Write the negation of the following statement in terms of symbols :
A necessary condition that two triangles are equivalent is that they have the same area.
View SolutionIt is not convenient to use a spherical Gaussian surface to find the electric field due to an electric dipole using Gauss’s theorem because
View Solution
Knowledge Check
The necessary condition for validity of Boyle's law is
AisothermalBisobaricCadiabaticDcircleAssertion: There is a solid metallic sphere. When some charge is given to the sphere then it is found that charge gets distributed uniformly on the outer surface of the sphere.
Reason: Electric field intensity inside the metallic volume is zero everywhere in electrostatic condition, hence for Gaussian surface of any shape inside the metallic volume, electric flux will always be zero. According to Gauss's law, the net enclosed charge is zero.AIf both assertion and reason are correct and reason is a correct explanation of the assertion .BIf both assertion and reason are correct but reason is not the correct explanation of assertionCIf assertion is correct but reason is incorrectDIf assertion is incorrect but reason is correct.Assertion: No net charge can exist in the region where electric field is uniform.
Reason: For any type of Gaussian surface selected within the region of a uniform electric field, the angle between electric field intensity and area normal is 90∘ everywhere. Hence, electric flux linked with the selected Gaussian surface is equal to zero. If the net electric flux is zero for some Gaussian surface then according to Gauss's law the net charge enclosed within the surface must be zero.AIf both assertion and reason are correct and reason is a correct explanation of the assertion .BIf both assertion and reason are correct but reason is not the correct explanation of assertionCIf assertion is correct but reason is incorrectDIf assertion is incorrect but reason is correct.
Using examples, prove that the conditiondydx=0 is neither a necessary nor a sufficient condition for a function y=f(x) to have a maximum or a minimumat a point.
View SolutionA charge Q is placed at the centre of an inaginary hemispherical surface. Using symmetry arguments and the Gauss's law, find the flux of the electric field due to this charge through the surface of the hemisphere (figure ).

View SolutionA charge Q is enclosed by a Gaussian surface. If surface area is doubled and charge Q is tripled then the outward electric flux will
View SolutionGauss's law and Coulomb's law , although expressed in different forms , are equivalent ways of describing the relation between charge and electric field in static conditions . Gauss's law is ε0ϕ=qencl,when q(encl) is the net charge inside an imaginary closed surface called Gaussian surface. The two equations hold only when the net charge is in vaccum or air .
A Gaussian surface encloses two of the four positively charged particles. The particles that contribute to the electric field at a point P on the surface are
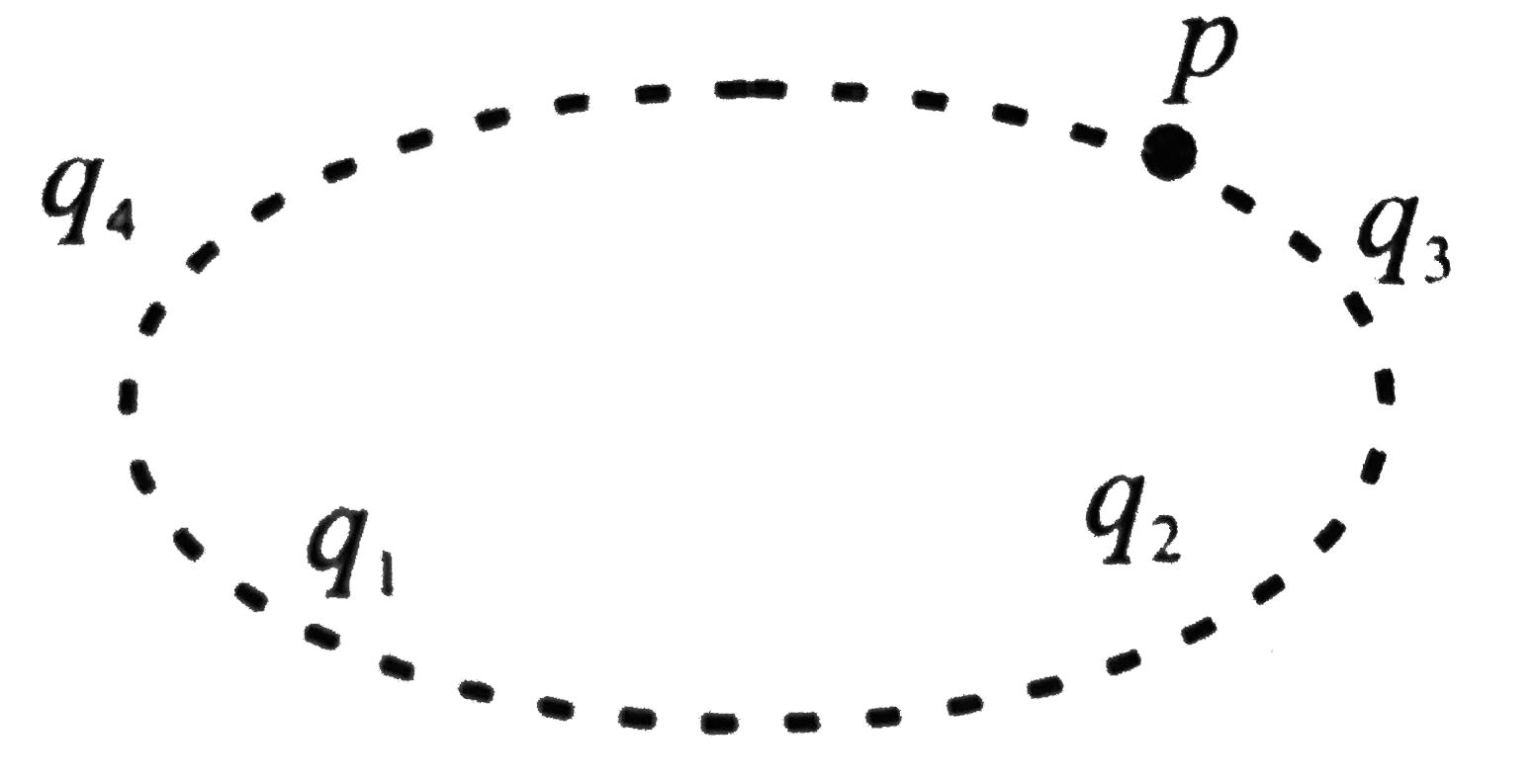
View SolutionA point charge of 1.77 μC is at the centre of a cubical gaussian surface having each side 50 cm. what is the net electric flux through the surface?
View Solution