What is the rms current through a resistor of 50Ω when an alternating voltage given by V140sin(314)t is connected to it?
1.5A
1.98A
2.5A
2.98A
The correct Answer is:B
To find the RMS current through a resistor of 50 ohms when connected to an alternating voltage given by V=140sin(314t), we can follow these steps:
Step 1: Identify the RMS Voltage
The given voltage is in the form V(t)=Vmsin(ωt), where Vm is the maximum voltage (amplitude) and ω is the angular frequency. Here, Vm=140 volts.
The RMS (Root Mean Square) voltage Vrms for a sinusoidal voltage is given by the formula:
Vrms=Vm√2
Step 2: Calculate the RMS Voltage
Substituting the value of Vm:
Vrms=140√2=1401.414≈98.99 volts
Step 3: Use Ohm's Law to Find RMS Current
Ohm's Law states that the current I through a resistor is given by:
I=VR
where V is the voltage across the resistor and R is the resistance.
Step 4: Substitute Values to Find RMS Current
Now substituting the values we have:
Irms=VrmsR=98.9950
Calculating this gives:
Irms≈1.9798 A
Step 5: Round the Answer
Rounding to two decimal places, we get:
Irms≈1.98 A
Thus, the RMS current through the resistor is approximately 1.98 A.
---
The given voltage is in the form V(t)=Vmsin(ωt), where Vm is the maximum voltage (amplitude) and ω is the angular frequency. Here, Vm=140 volts.
Vrms=Vm√2
Substituting the value of Vm:
Vrms=140√2=1401.414≈98.99 volts
Ohm's Law states that the current I through a resistor is given by:
I=VR
where V is the voltage across the resistor and R is the resistance.
Now substituting the values we have:
Irms=VrmsR=98.9950
Calculating this gives:
Irms≈1.9798 A
Rounding to two decimal places, we get:
Irms≈1.98 A
Topper's Solved these Questions
- SAMPLE PAPER 3Book:EDUCART PUBLICATIONChapter:SAMPLE PAPER 3Exercise:SECNTION -B
Explore 24 Videos
- SAMPLE PAPER 3Book:EDUCART PUBLICATIONChapter:SAMPLE PAPER 3Exercise:SECNTION -C
Explore 6 Videos
- SAMPLE PAPER 2Book:EDUCART PUBLICATIONChapter:SAMPLE PAPER 2Exercise:SECTION-C
Explore 6 Videos
- SAMPLE PAPER 5Book:EDUCART PUBLICATIONChapter:SAMPLE PAPER 5Exercise:SECTION - C
Explore 6 Videos
Similar Questions
How much current will flow through a resistor of resistor of resistance 12Ω if a battery of 18 V is connected across it ?
View SolutionAn ideal voltmeter V is connected to a 2.0Ω resistor and a battery with emf 5.0V and internal resistance 0.5Ω as shown in figure
(a) What is the current in the 2.0Ω resistor?
(b) What is the terminal voltage of the battery?
(c) What is the reading of the voltmeter?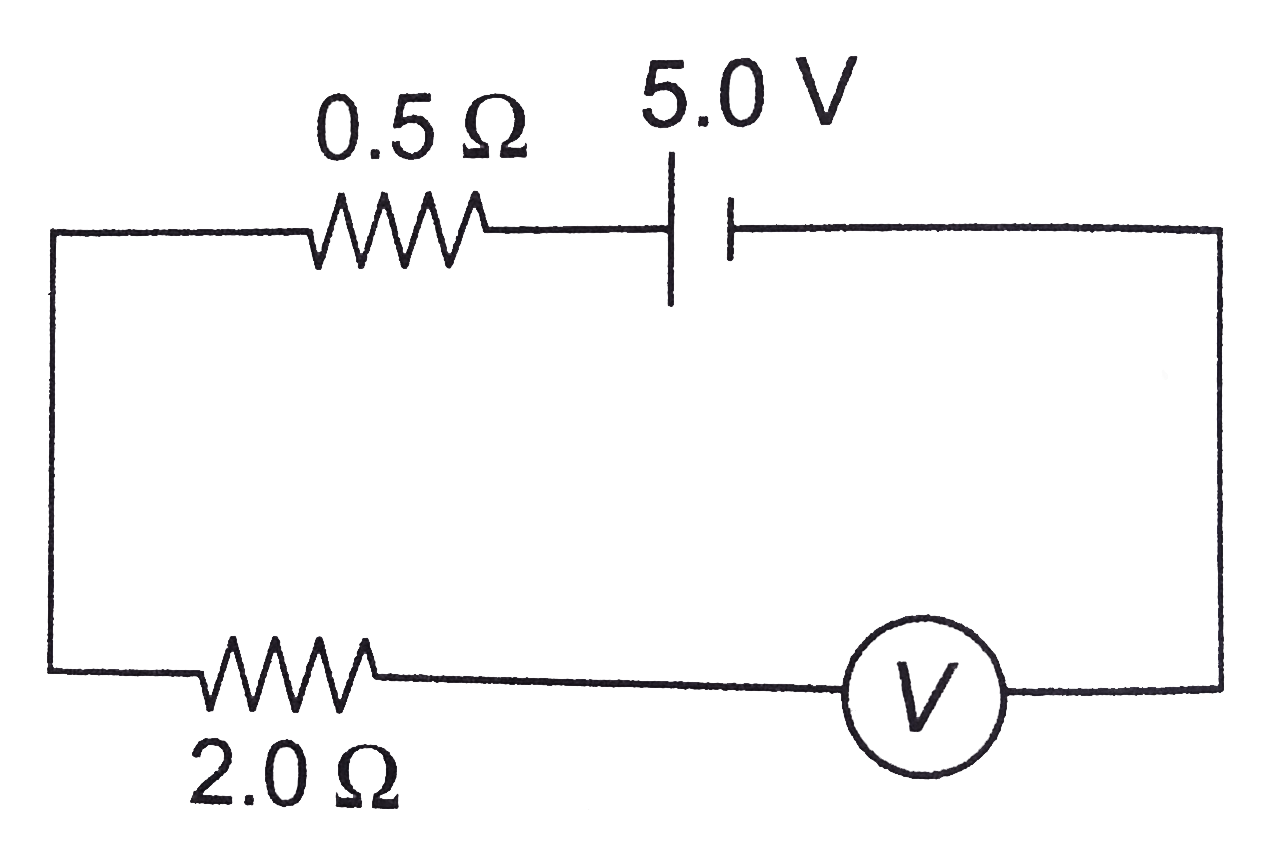
View Solution
Knowledge Check
What is the rms current through bulb rated 100 W for 220 V ac supply of 50 Hz?
A0.1 AB50 AC0.9 AD0.45 AWhat is the rms current through bulb rated 100 W for 220 V ac supply of 50 Hz?
A0.1 AB50 AC0.9 AD0.45 AFind the frequency of voltage for an AC circuit. The equation of alternating voltage is V=200sin314t.
A50 HzB60 HzC55 HzD65 Hz
A resistor of resistance 100Ω is connected across an alternate power source given by V = 100 sin 3.14 t . Calculate the rms value of current and frequency of the source.
View SolutionA 10 muF capacitor, an inductor and a resistor of 100Omega are connected to an alternating source of emf 200sqrt2 sin 100t as shown in the figure. What is the r.m.s current in the circuit and the value of the inductance if the current and the source voltage attain their maxima simultaneously? What is the average power consumed in this case
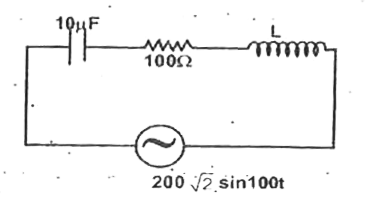
View SolutionWhen a battery connected across a resistor of 16Ω, the voltage across the resistor is 12 V. When the same battery is connected across a resistor of 10Ω, voltage across it is 11 V. The internal resistance of the battery (in ohm) is
View SolutionWhen a battery connected across a resistor of 16Ω the voltage across the resistor is 12 V. When the same battery is connected across a resistor of 10Ω voltage.
Across it is 11 V. The internal resistance of the battery in ohms is
View SolutionWhen a battery connected across a resistor of 16Ω, voltage across the resistor is 12V. When the same battery is connected across a resistor of 10Ω, voltage across it is 11 V. The internal resistance of the battery (in ohm) is
View Solution