Value of impedance of series LCR circuit is given by:
The correct Answer is:B
To find the impedance of a series LCR (Inductor-Capacitor-Resistor) circuit, we can follow these steps:
Step 1: Understand the Components
In a series LCR circuit, we have three components:
- Resistor (R)
- Inductor (L) with inductive reactance XL
- Capacitor (C) with capacitive reactance XC
Step 2: Identify Reactances
The inductive reactance XL is given by the formula:
XL=2πfL
where f is the frequency of the AC source and L is the inductance.
The capacitive reactance XC is given by:
XC=12πfC
where C is the capacitance.
Step 3: Determine the Phase Relationship
In a series LCR circuit, the inductive reactance and capacitive reactance are out of phase with each other. This means that:
- If XL>XC, the circuit behaves more like an inductor.
- If XC>XL, the circuit behaves more like a capacitor.
Step 4: Calculate the Net Reactance
The net reactance X of the circuit can be calculated as:
X=XL−XC(if XL>XC)
or
X=XC−XL(if XC>XL)
Step 5: Write the Impedance Formula
The total impedance Z of the circuit is given by:
Z=√R2+X2
where X is the net reactance calculated in the previous step.
Step 6: Final Expression
Thus, we can express the impedance in terms of the reactances:
Z=√R2+(XL−XC)2(if XL>XC)
or
Z=√R2+(XC−XL)2(if XC>XL)
Conclusion
The impedance of a series LCR circuit can be summarized as:
Z=√R2+(XL−XC)2
In a series LCR circuit, we have three components:
- Resistor (R)
- Inductor (L) with inductive reactance XL
- Capacitor (C) with capacitive reactance XC
The inductive reactance XL is given by the formula:
XL=2πfL
where f is the frequency of the AC source and L is the inductance.
XC=12πfC
where C is the capacitance.
In a series LCR circuit, the inductive reactance and capacitive reactance are out of phase with each other. This means that:
- If XL>XC, the circuit behaves more like an inductor.
- If XC>XL, the circuit behaves more like a capacitor.
The net reactance X of the circuit can be calculated as:
X=XL−XC(if XL>XC)
or
X=XC−XL(if XC>XL)
The total impedance Z of the circuit is given by:
Z=√R2+X2
where X is the net reactance calculated in the previous step.
Thus, we can express the impedance in terms of the reactances:
Z=√R2+(XL−XC)2(if XL>XC)
or
Z=√R2+(XC−XL)2(if XC>XL)
The impedance of a series LCR circuit can be summarized as:
Z=√R2+(XL−XC)2
Topper's Solved these Questions
- SAMPLE PAPER 2Book:EDUCART PUBLICATIONChapter:SAMPLE PAPER 2Exercise:SECTION-C
Explore 6 Videos
- SAMPLE PAPER 2Book:EDUCART PUBLICATIONChapter:SAMPLE PAPER 2Exercise:SECTION-C
Explore 6 Videos
- SAMPLE PAPER 04 (SOLVED)Book:EDUCART PUBLICATIONChapter:SAMPLE PAPER 04 (SOLVED)Exercise:SECTION-C
Explore 6 Videos
- SAMPLE PAPER 3Book:EDUCART PUBLICATIONChapter:SAMPLE PAPER 3Exercise:SECNTION -C
Explore 6 Videos
Similar Questions
Knowledge Check
In a series LCR circuit
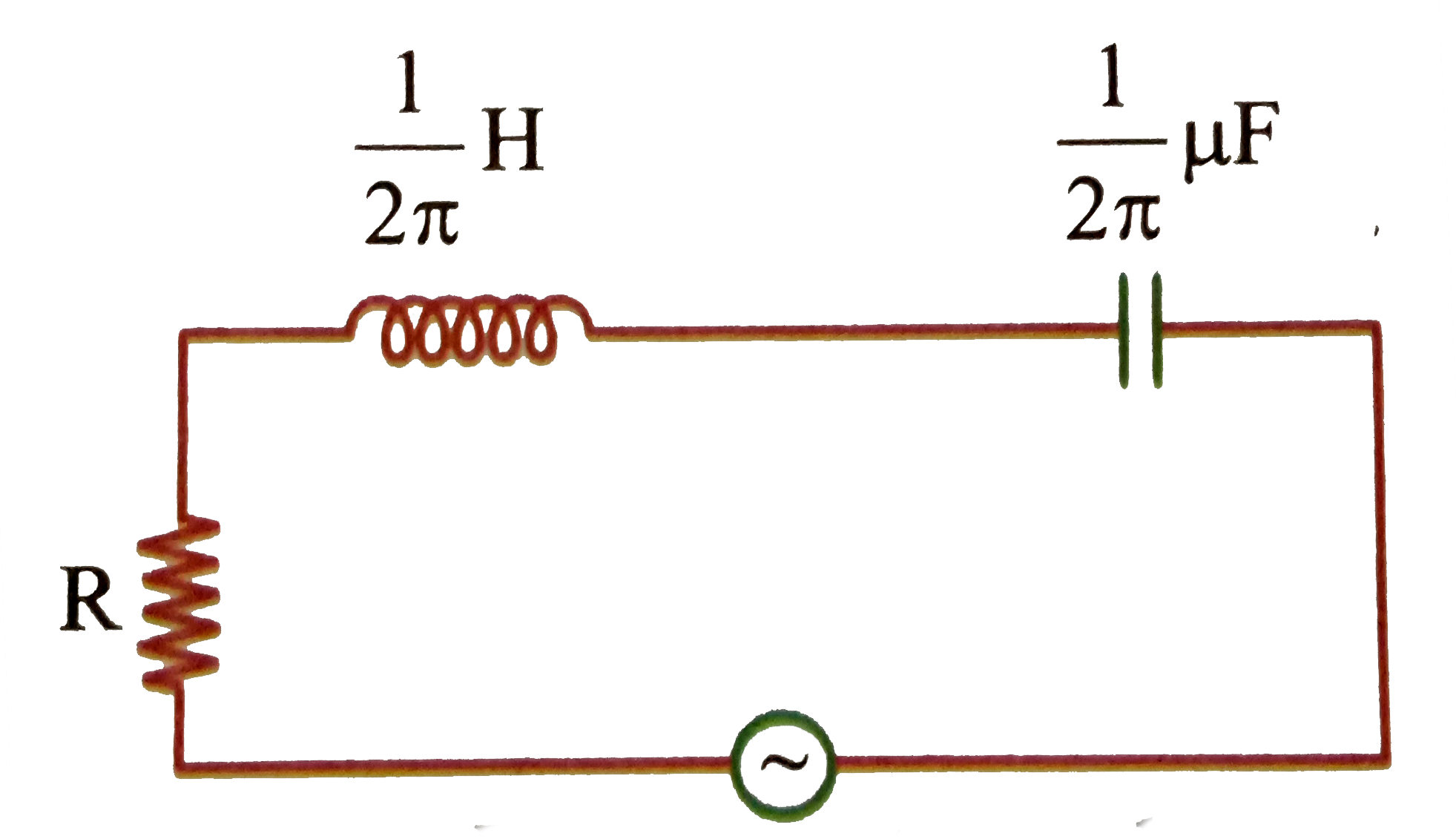 Athe voltage VL across the inductance leads the current in the circuit by a phase angle of π/2Bthe voltage VC across the capacitance lags behind the current by a phase angle of π/2Cthe voltage VR across the resistance is in phase with the currentDthe voltage across sereis combination of L, C and R is V=VL+VC+VR
Athe voltage VL across the inductance leads the current in the circuit by a phase angle of π/2Bthe voltage VC across the capacitance lags behind the current by a phase angle of π/2Cthe voltage VR across the resistance is in phase with the currentDthe voltage across sereis combination of L, C and R is V=VL+VC+VRthe impedance Z in an AC circuit is given by
AZ=√R2+(XC−XL)2BZ=√R2+3(XL−XC)2CZ=√R2−(XC+XL)2DZ=√R2+2(XL−XC)2At resonance frequency the impedance in series LCR circuit is
AmaximumBminimumCzeroDinfinity
The impedance of a series LCR circuit is 8 ohm when v=60Hz at resonance. At v=80Hz, the impedance is 10 ohm. Calculate the values of inductance L and capacitance C.
View SolutionWhat is the value of impedance of a resonant series LCR circuit?
View SolutionDetermine the impedance of a series LCR - circuit if the reactance of C and L are 250Ω and 220Ω respectively and R is 40Ω
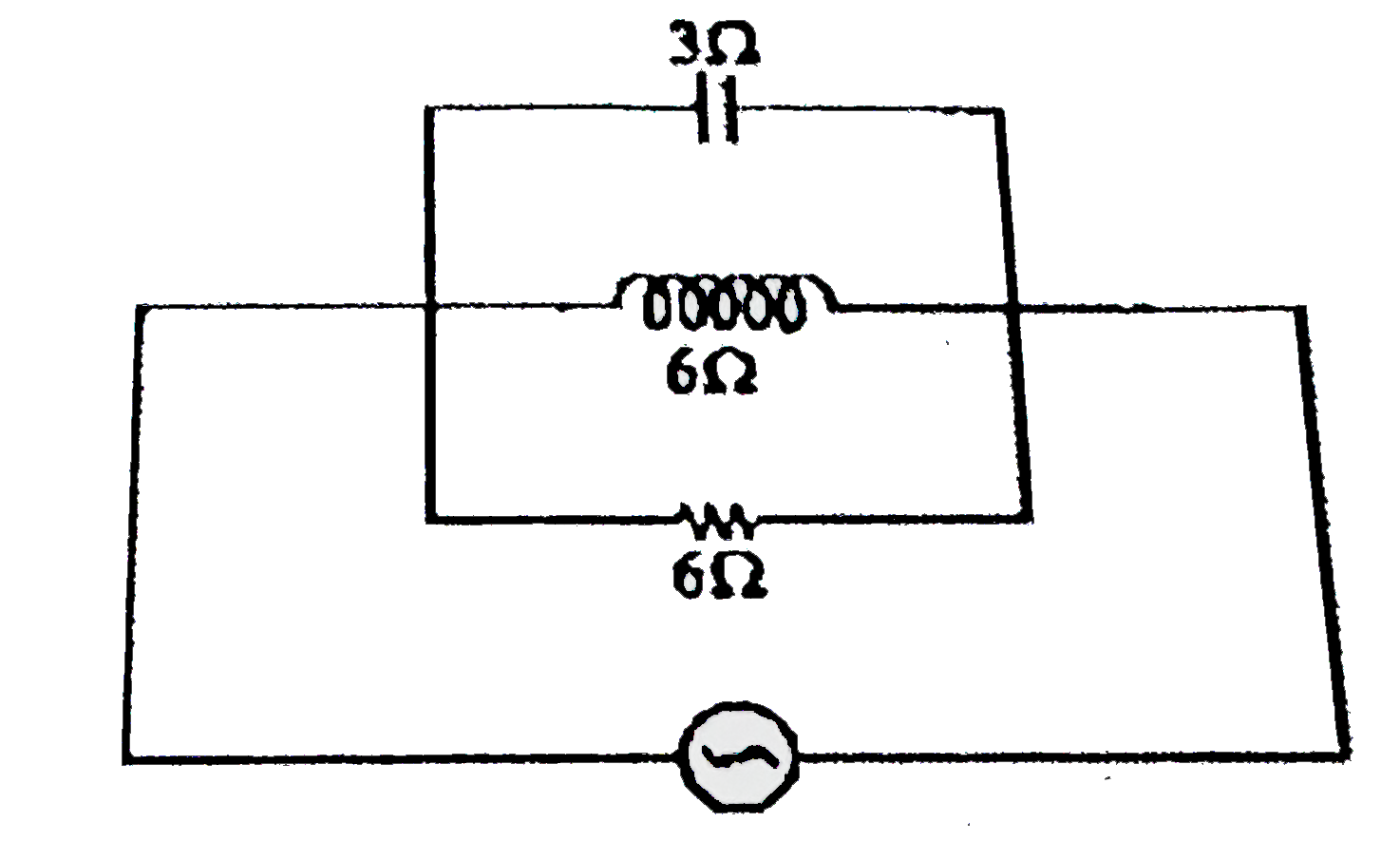
View SolutionFind out impedance of given circuit.
View Solutionwhat is resonance in series LCR circuit ?
View Solution