Question

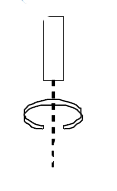
Copper ring is held horizontally on a magnet and is dropped through the ring with its length along the axis of the ring. The acceleration of magnet falling is:

Options

A. less than that due to gravity
B. equal than that due to gravity
C. more than that due to gravity
D. depends on diameter of the ring and length of the magnet

Answer

A

Explanation

To solve the problem of the acceleration of a magnet falling through a copper ring, we can follow these steps:

Step 1: Understand the Setup
We have a copper ring held horizontally, and a bar magnet is dropped through it with its length aligned along the axis of the ring.

Hint: Visualize the setup to understand how the magnet and the ring are positioned relative to each other.

Step 2: Identify the Forces Acting on the Magnet
As the magnet falls, the gravitational force acting on it is \( mg \) (where \( m \) is the mass of the magnet and \( g \) is the acceleration due to gravity).

Hint: Remember that the force of gravity is always acting downwards on the magnet.

Step 3: Induction of Current in the Copper Ring
When the magnet falls through the ring, it changes the magnetic flux through the ring, which induces an electromotive force (emf) according to Faraday's law of electromagnetic induction. This induced emf causes a current to flow in the ring.

Hint: Recall that a changing magnetic field induces a current in a conductor.

Step 4: Determine the Direction of the Induced Current
The direction of the induced current can be determined using Lenz's law. Since the magnet is falling, the induced current will flow in such a way as to oppose the change in magnetic flux. This typically results in an anticlockwise current when viewed from the top of the ring.

Hint: Use the right-hand rule to determine the direction of the induced current based on the motion of the magnet.

Step 5: Analyze the Forces on the Magnet
The induced current in the ring creates a magnetic field that interacts with the falling magnet. The interaction between the magnetic field created by the induced current and the magnet results in a repulsive force acting on the magnet.

Hint: Consider how the magnetic fields interact: the induced magnetic field opposes the motion of the magnet.

Step 6: Set Up the Equation of Motion
The net force acting on the magnet can be expressed as:
\( F_{\text{net}} = mg - F_{\text{repulsion}} \)
where \( F_{\text{repulsion}} \) is the force due to the induced current in the ring.

Using Newton's second law, we can write:
\( mg - F_{\text{repulsion}} = ma \)
where \( a \) is the acceleration of the magnet.

Hint: Remember that the net force is equal to mass times acceleration.

Step 7: Solve for the Acceleration
Rearranging the equation gives us:
\( a = g - \frac{F_{\text{repulsion}}}{m} \)
This indicates that the acceleration of the magnet is less than \( g \) due to the opposing force from the induced current.

Hint: The presence of the ring reduces the acceleration of the magnet compared to free fall.

Conclusion
The final result shows that the acceleration of the magnet falling through the copper ring is less than \( g \) due to the opposing force created by the induced current in the ring.

Final Answer: The acceleration of the magnet falling through the copper ring is less than \( g \).

---