The carner points of the feasible region formed by the system of linear inequations x−y≥−1,−x+y≥0,x+y≤2andx,y≥0, are
(0,0),(−1,0),(0,1)
(0,0),(2,0),(1,1)
(0,1),(1,1),(0,0)
(0,0),(1,1),(12,32),(0,1)
The correct Answer is:D
To find the corner points of the feasible region formed by the given system of linear inequalities, we will follow these steps:
Step 1: Write the inequalities
The system of inequalities is:
1. x−y≥−1
2. −x+y≥0 (or y≥x)
3. x+y≤2
4. x≥0
5. y≥0
Step 2: Convert inequalities to equations
To find the boundary lines, we convert the inequalities into equations:
1. x−y=−1
2. −x+y=0 (or y=x)
3. x+y=2
Step 3: Find the intersection points of the lines
We will find the intersection points of these lines:
Intersection of Line 1 and Line 2:
1. From x−y=−1 (Line 1) and y=x (Line 2):
x−x=−1⟹0=−1 (no solution)
Intersection of Line 1 and Line 3:
2. From x−y=−1 (Line 1) and x+y=2 (Line 3):
x−y=−1(1)x+y=2(2)
Adding (1) and (2):
2x=1⟹x=12
Substituting x=12 into (2):
12+y=2⟹y=2−12=32
So, the intersection point is (12,32).
Intersection of Line 2 and Line 3:
3. From y=x (Line 2) and x+y=2 (Line 3):
x+x=2⟹2x=2⟹x=1
Substituting x=1 into y=x:
y=1
So, the intersection point is (1,1).
Step 4: Identify the corner points
The corner points of the feasible region are:
1. The origin (0,0) (from x≥0 and y≥0).
2. The point (0,1) (from the line x−y=−1 when x=0).
3. The point (12,32) (intersection of Line 1 and Line 3).
4. The point (1,1) (intersection of Line 2 and Line 3).
5. The point (2,0) (from the line x+y=2 when y=0).
Step 5: List the corner points
The corner points of the feasible region are:
1. (0,0)
2. (0,1)
3. (12,32)
4. (1,1)
5. (2,0)
Conclusion
The corner points of the feasible region formed by the given system of linear inequalities are:
- (0,0)
- (0,1)
- (12,32)
- (1,1)
- (2,0)
The system of inequalities is:
1. x−y≥−1
2. −x+y≥0 (or y≥x)
3. x+y≤2
4. x≥0
5. y≥0
To find the boundary lines, we convert the inequalities into equations:
1. x−y=−1
2. −x+y=0 (or y=x)
3. x+y=2
We will find the intersection points of these lines:
1. From x−y=−1 (Line 1) and y=x (Line 2):
x−x=−1⟹0=−1 (no solution)
2. From x−y=−1 (Line 1) and x+y=2 (Line 3):
x−y=−1(1)x+y=2(2)
Adding (1) and (2):
2x=1⟹x=12
Substituting x=12 into (2):
12+y=2⟹y=2−12=32
So, the intersection point is (12,32).
3. From y=x (Line 2) and x+y=2 (Line 3):
x+x=2⟹2x=2⟹x=1
Substituting x=1 into y=x:
y=1
So, the intersection point is (1,1).
The corner points of the feasible region are:
1. The origin (0,0) (from x≥0 and y≥0).
2. The point (0,1) (from the line x−y=−1 when x=0).
3. The point (12,32) (intersection of Line 1 and Line 3).
4. The point (1,1) (intersection of Line 2 and Line 3).
5. The point (2,0) (from the line x+y=2 when y=0).
The corner points of the feasible region are:
1. (0,0)
2. (0,1)
3. (12,32)
4. (1,1)
5. (2,0)
The corner points of the feasible region formed by the given system of linear inequalities are:
- (0,0)
- (0,1)
- (12,32)
- (1,1)
- (2,0)
Topper's Solved these Questions
- BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 6 EXERCISE - SECTION - C9videos
SAMPLE PAPER 6
- BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 6 EXERCISE - SECTION - C9videos
SAMPLE PAPER 6
- BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 4 EXERCISE - SECTION - C7videos
SAMPLE PAPER 4
- BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 7EXERCISE - SECTION -C10videos
SAMPLE PAPER 7
Similar Questions
The corner points of the feasible region of the system of linear inequations x+y≥2,x+y≤5,x−y≥0,x,y≥0 are :
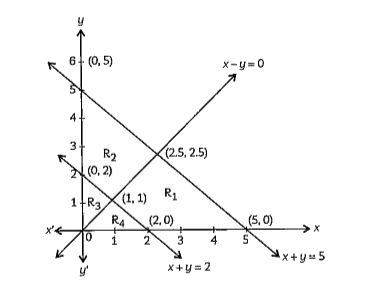 View Solution
View SolutionThe corner points of the feasible region determined by the following system of linear inequalities:
2x+y≥10,x+3y≤15,x,y≥0 are (0,0),(5,0),(3,4) and (0,5). Let Z=px+qy, where p,q≥0. Condition on p and q so that the maximum of Z occurs at both (3,4) and (0,5) is:
(a) p=q (b) p=2q (c) p=eq (d) q=3pView Solution
Knowledge Check
- Question 1 - Select One
The feasible region of the system of linear inequations x+2y≤120,x+y≥60,x−2y≥0,x,y≥0:
Ais bounded and lies in first quadrant .Bis unbounded and lies in first quadrant.Cdoes in first quadrant .Ddoes not exist. - Question 2 - Select One
The solution set of the inequations x≤4,x−y≥0,3x+y≥0
Alies in first and second quadrantsBlies in second and third quadrantsClies in third and fourth quadrantsDlies in fourth and first quadrants - Question 3 - Select One
The solution set of linear constraints x−2y≥0,2x−y≤−2 and x,y≥0 is
A(−43,−23)B(1,1)C(0,23)D(0,2)
The solution of linear inequalities x+y≥5andx−y≤3 lies
View SolutionA vertex of the linear in equalities 2x+3y≤6,x+4y≤4 and x,y≥0, is
View SolutionThe vertex of the linear inequalities 2x+3y≤6,x+4y≤4,x≥0,y≥0 is
View SolutionSolution set of inequalities x−2y≥0,−2x−y+2≤0,x≥0,y≥0
View SolutionA vertex of a feasible region by the linear constraints 3x+4y≤18,2x+3y≥3 and x,y≥0, is
View Solution
