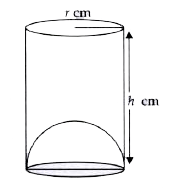
The capacity of a cylindrical vessesl with a hemispherical portion raised upwards at the bottom as shown in the given figure is $\frac{π r^{2}}{3} [3 h - 2 r]$ .

Video Solution

Text Solution

Verified by Experts

The correct Answer is:True

Updated on:21/07/2023

|

Answer

Step by step video, text & image solution for The capacity of a cylindrical vessesl with a hemispherical portion raised upwards at the bottom as shown in the given figure is (pi r^(2))/(3) [3h - 2r]. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.

Updated on:21/07/2023

Class 10 MATHS SURFACE AREAS AND VOLUMES

Topper's Solved these Questions

Similar Questions

Knowledge Check

Magnetic field in cylindrical region of radius $R$ in inward direction is as shown in figure.

Aan electron will expereince no force kept is $(2 R, 0, 0)$ if magnetic field increases with time
Bin the above situation, electron will experience the force in negative y-axis
Cif a proton is kept at $(0, \frac{R}{2}, 0)$ and magnetic field is decreasing then it will experience the force in positive x-direction
Dif a proton is kept at $(- R, 0, 0)$ and magnetic field is increasing then it will experience force in negative y-axis
From a solid sphere of mass M and radius R, a spherical portion of radius R/2 is removed, as shown in the figure Taking gravitational potential $V = 0 a t r = \infty,$ the potential at (G = gravitational constatn)

A $\frac{- 2 G M}{3 R}$
B $\frac{- 2 G M}{R}$
C $\frac{- G M}{2 R}$
D $\frac{- G M}{R}$
In the circuit shown in the given figure, the resistances $R_{1} and R_{2}$ are respectively

A $14 Ω and 40 Ω$
B $40 Ω and 44 Ω$
C $40 Ω and 30 Ω$
D $14 Ω and 30 Ω$

EDUCART PUBLICATION-SURFACE AREAS AND VOLUMES-OBJECTIVE TYPE QUESTIONS (TRUE OR FALSE)

Home
Ask Doubt
Profile