In a single component condensed system if degree of freedom is zero maximum number of phase that can co exist
0
1
2
3
The correct Answer is:D
To solve the problem of determining the maximum number of phases that can coexist in a single component condensed system when the degree of freedom is zero, we can use the Gibbs phase rule. Here is a step-by-step solution:
1. Understand the Gibbs Phase Rule: The Gibbs phase rule is given by the formula:
F=C−P+2
where:
- F = degree of freedom
- C = number of components
- P = number of phases
2. Identify the Variables: In this problem:
- The degree of freedom F=0 (as given in the question).
- The number of components C=1 (since it is a single component system).
3. Substitute the Known Values: Plug the values of F and C into the Gibbs phase rule equation:
0=1−P+2
4. Simplify the Equation: Rearranging the equation gives:
0=3−P
This can be rewritten as:
P=3
5. Conclusion: The maximum number of phases P that can coexist in a single component condensed system with a degree of freedom of zero is 3.
Final Answer:
The maximum number of phases that can coexist is 3.
---
F=C−P+2
where:
- F = degree of freedom
- C = number of components
- P = number of phases
- The degree of freedom F=0 (as given in the question).
- The number of components C=1 (since it is a single component system).
0=1−P+2
0=3−P
This can be rewritten as:
P=3
The maximum number of phases that can coexist is 3.
Similar Questions
Knowledge Check
The system that contains the maximum number of atoms is
A4.25 g of NH3B8 g of O2C2g of H2D4 g of HeThe number of phases in colloidal system are
A1B2C3D4The number of degrees of freedom of molecules of argon gas is
A1B2C3D6
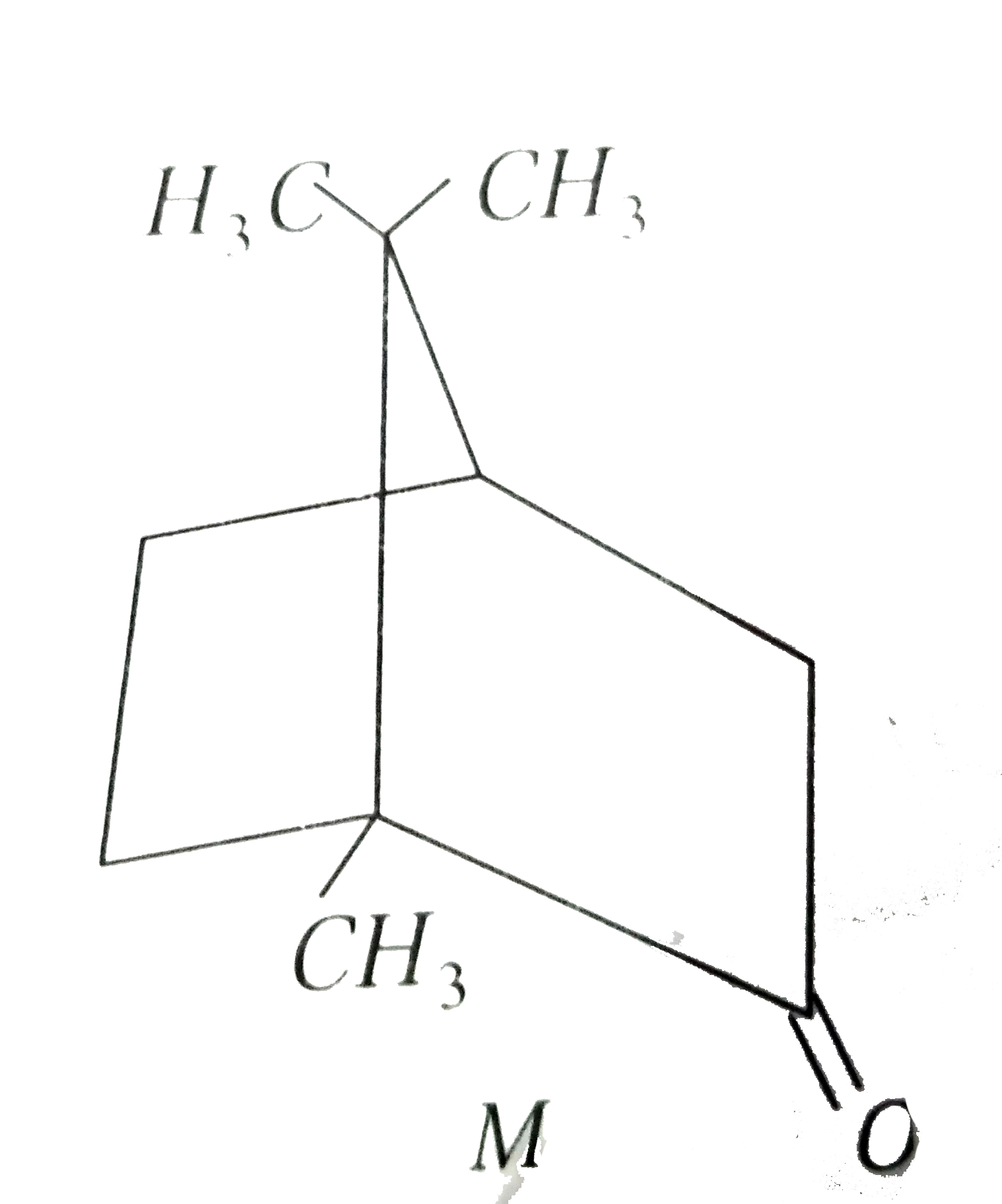
The total number of stereoisomers that can exist for M is

View SolutionThe total number of stereoisomers that can exist for M is

View SolutionThe total number of stereoisomers that can exist for M is
View SolutionIn a town, the car plate numbers contain only three or four digits, not containing the dit 0. What is the maximum numbers of cars that can be numbered?
View SolutionMaximum number of existing transgenic animals is
View Solution